概率相关
概率与期望
\(u\)若\(X\)是一个离散型的随机变量,可能值为\(x_1,x_2…,\)对应的概率分别为\(p_1,p_2…,\)那么它的期望值为
一些结论
1.\(E(X+Y)=E(X)+E(Y)\)
2.\(E(aX)=aE(X)\)
3.随机变量(表达式)\(X\)与\(Y\)独立时,\(E(XY)=E(X)E(Y)\)
条件概率
\(P(A|B)=\frac{P(AB)}{P(B)}[P(A|B)此处表示在B事件发生的情况下A发生的概率;P(AB)表示AB同时发生的概率]\)
\(ex:贝叶斯公式P(A|B)=\frac{P(B|A)P(A)}{P(B)}\)
方差相关
\(Var(x)=E(X^2)-E(X)^2\)
概率生成函数(PGF)
\(F(z)=\sum_{i=0}^\infty P(X=i)z^i\)
-
\(F(1)=1\)
证明:
\(F(1)=\sum_{i=0}^\infty p_i\),因为\(X\)为正整数域上的随机变量,故为\(1\)
-
\(E(X)=F'(1)\)
证明:
\(F'(1)=\sum_{i=1}^\infty p_{i}i=E(X)\)
-
\(E(X^{\underline{k}})=F^{(k)}(1)\)
证明:
\(F^{(k)}(1)=\sum_{i=k}^\infty p_ii^{\underline k}=E(X^{\underline k})\)
因果乃旋转纺车,光彩之多面明镜
浮世苍茫,不过瞬逝幻梦
善恶爱诳,皆有定数
于命运之轮中
吞噬于黄泉之冥暗
呜呼,吾乃梦之戍人
幻恋之观者
唯于万华镜中,永世长存
浮世苍茫,不过瞬逝幻梦
善恶爱诳,皆有定数
于命运之轮中
吞噬于黄泉之冥暗
呜呼,吾乃梦之戍人
幻恋之观者
唯于万华镜中,永世长存

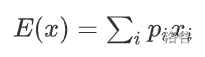

 浙公网安备 33010602011771号
浙公网安备 33010602011771号