The Child and Polygon

考虑区间dp

\(dp_{i,j}\)表示\(i\)点到\(j\)点所截下来的图形的方案数，如下图中阴影部分的划分方案数

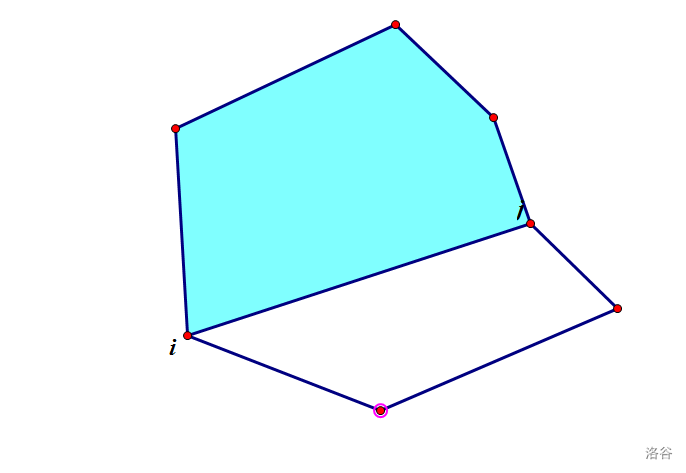
\(dp_{i,j}=\sum\limits_{x=i+1}^{j-1}dp_{i,x}dp_{x,j},\)表示先以\(ij\)为\(1\)边剖出一个三角形，再按照乘法原理与加法原理得到结果,如下图

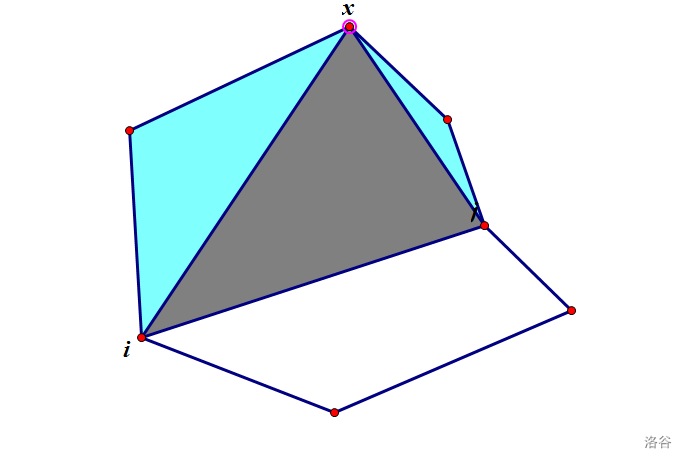
转移条件为\(x\)点在\(ji\)的右边，如上图,用叉乘判断

\(\overrightarrow{ij} \times \overrightarrow{ix}>0\)时\(x\)在\(ji\)右边

\(\mathfrak{Talk\ is\ cheap,show\ you\ the\ code.}\)

#include<map>
#include<queue>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
# define ll long long
# define read read1<int>()
# define Type template<class T>
Type T read1(){
    T t=0;
    bool vis=0;
    char k;
    do (k=getchar())=='-'&&(vis=1);while('0'>k||k>'9');
    while('0'<=k&&k<='9')t=(t<<3)+(t<<1)+(k^'0'),k=getchar();
    return vis?-t:t;
}
Type void print(T arg1){cout<<arg1;}
Type void get(T arg1){cout<<arg1;}
template<typename T,typename... Ts>
    void print(T arg1, Ts... arg_left){
        cout<<arg1<<" ";
        print(arg_left...);
    }
template<typename T,typename... Ts>
    void get(T arg1, Ts... arg_left){
        cout<<arg1<<" ";
        print(arg_left...);
    }
# define mod 1000000007
# define A pair<int,int>
A a[205];
int s,dp[205][205];
A operator -(const A &x,const A &y){return A(x.first-y.first,x.second-y.second);}
ll operator *(const A &x,const A &y){return 1ll*x.first*y.second-1ll*x.second*y.first;}
int main(){
    s=read;ll t=0;
    for(int i=1;i<=s;++i){
        a[i]=make_pair(read,read);
        if(i!=1)t+=a[i-1]*a[i];
    }
    t+=a[s]*a[1];
    for(int i=1;i<s;++i)
        dp[i][i+1]=1;
    if(t>0)reverse(a+1,a+s+1);
    for(int i=s;--i;)
        for(int j=i+2;j<=s;++j)
            for(int k=i+1;k<j;++k)
                if((a[j]-a[i])*(a[k]-a[i])>0)
                    dp[i][j]=(dp[i][j]+1ll*dp[i][k]*dp[k][j])%mod;
    printf("%d",dp[1][s]);
    return 0;
}