斐波拉契数列的求法分析

                                                斐波拉契数列
                                已知有1数列，F[i]={F[i-1]+F[i-2]   i>2
                                		    F[i]=1               i<=2
                                		求F[n]?

法1：动态规划

直接根据题意,F[i]=F[i-1]+F[i-2]

#include<cstdio>
int main()
{
	int n;
	scanf("%d",&n);
	const int m=n;
	auto long long a[m+1];
	a[1]=a[2]=1;
	for(int i=3;i<=n;++i)a[i]=a[i-1]+a[i-2];
	printf("%lld",a[n]);
	return 0;
}

然而，时空复杂度O（n），大数据容易MLE

法2：递归

#include<cstdio>
long long Fib(int n)
{
	if(n<3)return 1;
	return Fib(n-1)+Fib(n-2);
}
int main()
{
	int n;
	scanf("%d",&n);
	printf("%lld",Fib(n));
	return 0;
}

时间复杂度O（2^n），空间复杂度O（1），大数据一定TLE

法3：迭代法

我们可以发现，与F[i]有关的只有F[i-1]与F[i-2]，故可用迭代法

#include<cstdio>
int main()
{
	int n;
	long long a=1,b=1,t;
	scanf("%d",&n);
	while(--n)t=a,a=b,b+=t;
	printf("%lld",a);
	return 0;
}

时间复杂度O（n），空间复杂度O（1），可以过大部分数据

---

当然，如果你要追求完美，可以继续往下看--》

法4：平方分割法

首先，我们先计算如下的式子
F[i]=F[i-2]+F[i-1]=F[i-3]+2F[i-2]=2F[i-4]+3F[i-3]......
这时，我们假设当前为F[i]=a*F[j]+b*F[j-1]
则是不是F[i]=(a+b)*F[j-1]+a*F[j-2]

等等，系数是不是有点眼熟：1,1,2...a，b，a+b

这不正是斐波拉契数列吗? 所以，我们可以得到：F[i]=F[k]*F[i-k-1]+F[k+1]*F[i-k]

即F[k]*F[i]+F[k+1]*F[i+1]=F[i+k+1]

F[n+k]=F[k]*F[n-1]+F[k+1]*F[n]
F[n+k+1]=F[k]*F[n]+F[k+1]*F[n+1]
F[n+k-1]=F[n+k+1]-F[n+k]

#include<cstdio>
#include<cmath>
# define ll long long
void make(int n,ll &x,ll &y,ll &m)////x:Fib[n] ; y:Fib[n+1] ; m:Mod
{
    ll a,b,to[3]={0,1,1};
    ////特判
    if(n<2)
	{
		x=to[n];
		y=to[n+1];
		return;
	}
	if(n==2)
	{
		x=1;
		y=2;
		return;
	}
	////求k,并递归求解Fib[k]及F[k+1]
    ll k=sqrt(n);
    make(k,a,b,m);
    ////从Fib[k]到Fib[k*k]的变化
    for(int i=1;i<=k;++i)
    {
        to[2]=(to[1]*a+to[2]*b)%m;
        to[1]=(to[0]*a+to[1]*b)%m;
        to[0]=(to[2]-to[1])%m;
    }
    k*=k;
	////如果已经得到解（n为完全平方数），退出
    if(k==n)
	{
		x=(to[0]+m)%m;
		y=(to[1]+m)%m;
		return;
	}
	////如果没有，则从k*k迭代到n
    for(int i=k+1;i<=n;++i)
    {
        to[2]=to[1];
        to[1]=(to[0]+to[1])%m;
        to[0]=to[2];
    }
    x=(to[0]+m)%m;
    y=(to[1]+m)%m;
}
int main()
{
	ll n,m,x,y;
	scanf("%lld %lld",&n,&m);
	make(n,x,y,m);
	printf("%lld",x);
    return 0;
}

时间复杂度为O（n/k+k）,当k=sqrt(n)时取最小，得出结果O（sqrt(n)）

如果这都会TLE，则看看下面的

法5：矩阵加速


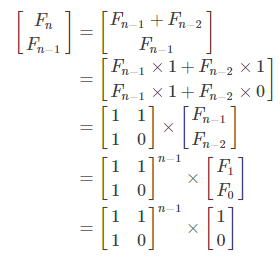#include<cstdio>
#include<iostream>
#include<vector>
using namespace std;
# define Type template<typename T>
Type inline T read1()
{
    T t=0;
    char k=getchar();
    bool flag=0;
    while('0'>k||k>'9')
    {
        if(k=='-')flag=1;
        k=getchar();
    }
    while('0'<=k&&k<='9')t=(t<<3)+(t<<1)+(k^48),k=getchar();
    return flag?-t:t;
}
# define ll long long
class Mat
{
    # define Vec vector<ll>
    # define Arr vector<Vec>
    Arr a;
    public:
        Mat(){}
        Mat(Arr k):a(k){}
        Mat(ll x,ll y){a.resize(x);for(ll i=0;i<x;++i)a[i].resize(y);}
        Vec& operator [](const ll k){return a[k];}
        ll wide(){return a.size();}
        ll len(){return a.empty()?0:a[0].size();}
        Mat operator *(Mat k)
        {
            Arr tem;
            tem.resize(wide());
            for(ll i=0;i<wide();++i)
            {
                tem[i].resize(k.len());
                for(ll j=0;j<len();++j)
                    for(ll l=0;l<k.len();++l)
                        tem[i][l]+=a[i][j]*k[j][l];
            }
            return Mat(tem);
        }
        Mat operator +(Mat k)
        {
            ll o=max(wide(),k.wide()),p=max(len(),k.len());
            Mat tem(o,p);
            for(ll i=0;i<o;++i)
                for(ll j=0;j<p;++j)
                {
                    if(i<wide()&&j<len())tem[i][j]=a[i][j];
                    if(i<k.wide()&&j<k.len())tem[i][j]+=k[i][j];
                }
            return tem;
        }
        Mat operator %(ll k)
        {
            Mat tem(wide(),len());
            for(ll i=0;i<wide();++i)
                for(ll j=0;j<len();++j)
                    tem[i][j]=a[i][j]%k;
            return tem;
        }
        Mat& operator %=(ll k){return *this=*this%k;}
        Mat& operator *=(Mat k){return *this=*this*k;}
        Mat& operator +=(Mat k){return *this=*this+k;}
        bool scan(ll x,ll y,const ll value)
        {
            if(x>=wide()||y>=len()||x<0||y<0)return 0;
            a[x][y]=value;
            return 1;
        }
    # undef Vec
    # undef Arr
};
Type T quickpow(T k,const ll n,ll Mod)
{
    if(n==1)return k;
    T tem=quickpow(k,n>>1,Mod);
    if(Mod!=0)
    {
        tem=(tem*tem)%Mod;
        if(n&1)tem=(tem*k)%Mod;
    }
    else
    {
        tem*=tem;
        if(n&1)tem*=k;
    }
    return tem;
}
# define read read1<ll>()
int main()
{
    ll n=read,l=read;
    if(n==1)return !putchar('1');
    Mat k(2,2);
    k[0][0]=k[0][1]=k[1][0]=1;
    k=quickpow(k,n-1,l);
    printf("%lld",k[0][0]);
    return 0;
}