浅谈二项式定理基础应用

基本技能

公式及原理

公式是次要的，需要明白公式的本质是组合数.

例如，\((a+b)^n\)，本质是 \(n\) 个 \((a+b)\) 相乘，那么对于每一项，有多少个括号提供 \(a\)，多少个括号提供 \(b\) 呢？显然，若有 \(r\) 个括号提供 \(a\)，则有 \((n-r)\) 个括号提供 \(b\).

进一步思考，已知有 \(r\) 个括号提供 \(a\)，\((n-r)\) 个括号提供 \(b\)，那么具体是哪几个呢？我们关心有多少种组合方式，每一种组合方式都可做出一个贡献，答案显然为 \(C_{n}^r\).

综上，我们可总结形如 \((a+b)^n\) 展开项的通项公式.

\[T_{r+1}=C_n^ra^{n-r}b^{r} \]

公式的形态和前文描述略有区别，由于展开时一般按照 \(a\) 次数从高到低排列，故这里做出相应调整，本质上是一样的.

常见的组合数公式如下.

• \(C_{n}^m=C_{n}^{n-m}\)

非常常用，\(n\) 个数中选 \(m\) 个数方案数等价于 \(n\) 个数中选 \(m-n\) 个数方案数. 二者互为补集.

• \(C^{m}_n+C^{m-1}_{n}=C^{m}_{n+1}\).

我们可这样理解，对于在 \(n+1\) 个数中选 \(m\) 个数方案数，将 \(a_1\) 单独考虑. 因为组合数的本质即为考虑每个数选或不选. 当第一个数选择时，只需在后面的数字中选出 \(m-1\) 个数即可. 若不选，需在后面 \(n\) 个数中选出 \(m+1\) 个数. 两种方案显然互斥.

二项式系数及相关结论

二项式系数 ：将二项式展开后，形如 \(C_n^0,C_n^1\dots C_n^n\) 的系数称为二项式系数. 其分布规律如下.

• 若 \(n\) 为奇数，展开式有 \(n+1\) 项，分布规律如图所示.
  

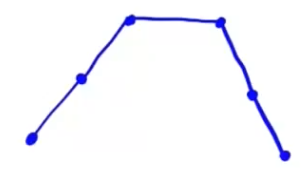
  最大项有两项.

• 若 \(n\) 为偶数，展开有偶数项，分布规律如图所示.

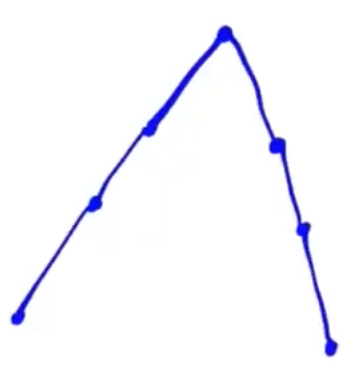
最大项有一项.

同时有

\[\sum\limits_{i=0}^n C_n^i=(1+1)^n \]

证明可通过逆推展开.

因为

\[0=(1-1)^n=C_n^0-C_n^1+C_n^2-C_n^3+\dots \]

所以

\[C_n^0+C_n^2+C_n^4+\dots = C_n^1+C_n^3+C_n^5=\dfrac{2^n}{2} \]

题型精练

例1.1 \((x^2+\dfrac 2 x)^6\) 的常数项是 ____.

Solution. 套公式题.

\[T_{r+1}=C_n^rx^{6-r}\left(\frac 2 x\right)^r \]

是常数项当且仅当 \(6-r=r\Leftrightarrow r=3\).

套用公式解决即可.

事实上，本题从二项式定理的原理，即幂运算的意义出发更加优美. \((x^2+\dfrac 2 x)^6\) 的意义为 \(6\) 个二项式相乘.对于展开后的常数项，每一个括号要么贡献 \(x^2\)，要么贡献 \(\dfrac 2 x\). 显然 \(x^2\) 需要两个，\(\dfrac 2 x\) 需要 \(4\) 个. 由此可知这是第 \(3\) 项，再套用公式即可.

---

例1.2-1 已知 \(\left(\dfrac{1}{x}+my\right)(2x-y)^5\) 的展开式中 \(x^2y^4\) 的系数为 \(40\)，求 \(m\).

Solution. 看到 \(5\) 次方，想到二项式定理. 考虑如何凑 \(x^2y^4\). 第一种方案是 \(\dfrac 1 x\cdot x^3y^4\). 但不存在该情况，因为 \(3+4\ne 5\). 那么只可能是 \(my\cdot x^2y^3\). 这是合法的.

此时，五个括号相乘，需两个括号提供 \(x\)，剩下三个括号提供 \(-y\). 我们从五个括号中挑两个提供 \(x\)，剩下的提供 \(-y\)，即

\[my\cdot C_5^2(2x)^2\cdot(-y)^3 \]

也就是 \(-40m=40\Rightarrow m=-1\).

---

例1.2-2 \(\left(x+\dfrac{y^2}{x}\right)(x+y)^5\) 的展开式中 \(x^3y^3\) 的系数是___.

Hint. 和上题同理，不过本题两种情况均可，此时需要加起来，原因显然.

---

例1.3-1 \((1+2x)^3(1-x)^4\) 展开式中 \(x^2\) 的系数是___.

Solution. 依然是分情况讨论. 两式中均没有分式，若 \((1+2x)^3\) 提供常数，则后者提供 \(x^2\)；若前者提供 \(x\)，后者提供 \(x\); 若前者提供 \(x^2\)，后者提供常数.

对于第一种情况，要想提供常数，三个括号都得提供常数 \(1\)，只有一种情况. 第二个式子要想提供 \(x^2\)，需要两个括号提供 \(-x\)，有 \(C_4^2\) 中情况. 即

\[C_3^31^3\times C_4^2\cdot 1^2\cdot(-x)^2=6x^2 \]

同理，第二种情况对应

\[C_3^1(2x)^2\cdot 1^2\times C_4^1(-x)^1\cdot 1^3=-24x^2 \]

第三种情况如下

\[C_3^2\cdot(2x)^2\cdot 1^1\times C_4^4\cdot 1^4=12x^2 \]

三种情况合并，答案是 \(-6x^2\).

事实上，本题还有另外一种通用性更强的解法，详见下题.

---

例1.3-2 \((1+\sqrt[3]{x})^6\left(1+\dfrac{1}{\sqrt[4]{x}}\right)^{10}\) 展开式的常数项是 ___.

Solution. 谁是常数呢？并不好想.

第一个括号，展开后是 \(7\) 项，第二个括号，展开后是 \(11\) 项. 乘起来有 \(77\) 项. 我们写出通项公式进行观察.

\[C_6^{r_1}\cdot 1^{6-r_1}\left(\sqrt[3]{x}\right)^{r_1}\cdot C_{10}^{r_2}1^{10-r_2}\cdot\left(\dfrac{1}{\sqrt[4]{x}}\right)^{r_2} \]

该通项公式代表了 \(77\) 项中的任何一项.

合并一下，即

\[C_6^{r_1}\cdot C_{10}^{r_2}x^{\dfrac{r_1}{3}-\dfrac{r_2}{4}} \]

是常数项当且仅当 \(\dfrac{r_1}{3}=\dfrac{r_2}{4}\Leftrightarrow 4r_1=3r_2\). 又因为 \(r_1,r_2\in\Z\)，得 \(3 | r_1,4| r_2\).

因此，\(r_1,r_2\) 有三种情况，分别是 \(\{(0,0),(3,4),(6,8)\}\). 只需计算

\[C_6^0\cdot C_{10}^0+C_6^3\cdot C_{10}^4+C_6^6\cdot C_{10}^8 \]

即可.

进一步的，对于两个二项式定理相乘，求某一次数的系数都可通过求通项公式，合并同类项，得 \(r_1,r_2\) 关系解决.

---

例1.4-1 已知

\[(1+x)^{10}=\sum\limits_{i=0}^{10} a_i(1-x)^i \]

求 \(a_8\).

Solution.

如果直接二项式定理展开，非常数项都是 \(x^n,n\in[1,10]\) 的形式.

所以需要凑，\((1+x)^{10}=[2-(1-x)]^{10}\). 此时再展开，就是右式形式了.

\(a_8\) 即要求 \((1-x)^8\)，需要两个括号提供 \(2\)，即

\[C_{10}^2 2^2\cdot(1-x)^8 \]

\[\Rightarrow a_8=180 \]

---

例1.4-2 已知

\[x^2+x^{10}=\sum\limits_{i=0}^{10} a_i(x+1)i \]

求 \(a_9\).

Solution. 和上题同理，左侧 \(x^2\rightarrow [(x+1)-1]^2,x^{10}\rightarrow [(x+1)-1]^{10}\). 也就是

\[[(x+1)-1]^2+[(x+1)-1]^{10}=\sum\limits_{i=0}^{10} a_i(x+1)i \]

此时，要想出现 \((x+1)^9\)，只能凑 \([(x+1)-1]^{10}\). 也就是

\[C_{10}^1(-1)^1(x+1)^9 \]

\[=-10(x+1)^9 \]

如果两个都合法的话，加起来即可. 比如求 \(a_2\).

---

例1.5 求

\[\sum\limits_{i=1}^9(1+x)^i \]

\(x^2\) 的系数.

SolutionA. 依据二项式定理，将所有项展开，不难发现答案为

\[\sum\limits_{i=2}^9 C_i^2 \]

可以一项一项算.

为简化计算，我们知道 \(C_n^m+C_n^{m-1}=C_{n+1}^m\). 不妨将 \(C_2^2\) 看作 \(C_3^3\)，进而应用上述公式逐步递推，得所求式等价于 \(C_{10}^3\).

SolutionB. 不难发现这是等比数列. 应用求和公式，式子等价于

\[\dfrac{(1+x)^2[1-(x+1)^8]}{1-(1+x)} \]

也就是

\[\dfrac{(x+1)^{10}-(x+1)^2}{x} \]

要想求 \(x^2\) 的系数，只需求 \((x+1)^{10}\) 中 \(x^3\) 系数即可. 显然答案为 \(C_{10}^3\).

---

例1.6-1 \((x^2+x+y)^5\) 中，\(x^5y^2\) 的系数为 ___.

Solution. 考虑如何凑出 \(x^5,y^2\).

不难想到，\(x^2\) 需要有两个贡献，\(x\) 需要有一个贡献，\(y\) 需要两个贡献，这样加起来总共五个贡献. 且只有这一种凑法.

也就是

\[C^2_5\left(x^2\right)^2\cdot C_3^1\cdot x^1\cdot C_2^2y^2 \]

这个式子是怎么得出来的呢？首先在 \(5\) 个括号中选 \(2\) 个括号贡献 \(x^2\)，再在剩下的三个括号中选一个括号贡献 \(x\)，最后在剩下的 \(2\) 个括号中选择 \(2\) 个贡献 \(y^2\). 和二项式的展开原理是一致的. 只不过由于第二项 \(C\) 值恒等于 \(1\) 我们一般忽略.

答案是 \(30\).

---

例1.6-2 若 \(\left(\dfrac{1}{\sqrt x}+ax^2+1\right)^5\) 展开后常数项为 \(5\)，求 \(a\).

Solution. 如何凑出常数项？也就是如何分配这 \(5\) 个贡献？一种方法是 \((0,0,5)\)，还有一种方法是 \((4,1,0)\).

对于第一种情况，答案为

\[C_5^5\cdot 1^5 \]

对于第二种情况，答案为

\[C_5^4\left(\dfrac{1}{\sqrt x}\right)^4\cdot(ax^2) \]

二者加起来即可. 处理思想都差不多.

像这样的题目有很多，核心思想都在于如何凑，如何分贡献.

---

例1.7 已知 \((1+x)^n\) 展开式中第四项与第八项的二项式系数相等，求奇数项的二项式系数.

Solution.

由题意得 \(C_n^3=C_n^7\)，所以 \(n=10\)，依据前文二项式系数相关引理，得奇数项二项式系数和为 \(\dfrac{2^{n}}{2}\)

---

例1.8 \(\left(x+\dfrac a x\right)\left(2x-\dfrac 1 x\right)^5\) 展开后各项系数和为 \(2\)，求该展开式中常数项.

Solution. 只需令 \(x=1\) 即可直接得展开后系数，即

\[(1+a)(2-1)^5=2 \]

解得 \(a=1\).

后面做法参见 例1.2，不再赘述.

1h 28min