定点数乘法

乘法相当于变为移位运算和求和运算，相当于将乘数B从低位到高位乘下来，部分积从零开始累加，并且右移一位（相当于乘了个1/2）

（注意，符号位相当于进行了异或运算，相同为0，相异为1，不参与后面的数值部分计算)

原码乘法：

 

补码乘法：Booth算法（被乘数，乘数符号任意） 一般用于带符号数乘法

这个的原理证明还是慢慢看吧，先大概把怎么用搞懂

计算规则：

 

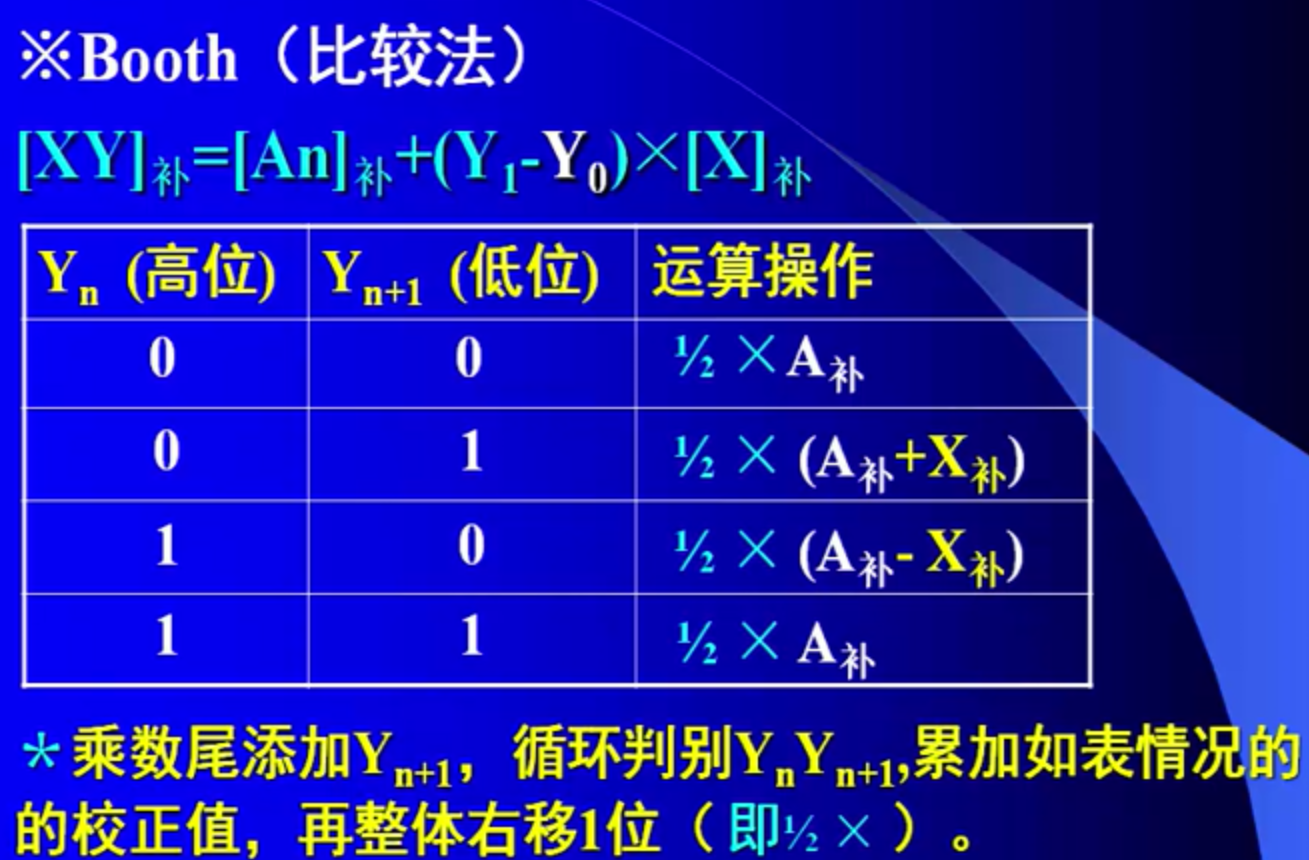
A_补 指累加的部分积

例：

 

 x = -0.1101  y = -0.1011

A = 00.0000 ，B = [x]补 = 11.0011  -B = -[x]补 = 00.1101    C = [Y]补 = 1.0101

在第一步之前，需要在C的最低位补上一个0(为什么)，使得C = 101010

第一步：

 判断C中最低两位的数 10，所以减去B，等于加上-B

此时A = 000000+001101=00 1101       C = 10 1010 (先不动，后面统一右移)   右移操作：

由于是双符号位表示，则需要将A中第二符号位右移，使其先暂时保持空缺，同时A中最低位右移到C最高位，如图所示

 

对A而言，当前是补码正数，所以在空缺的位置补0

第二步：判断C中最低两位的数，01，所以+B

A = 000110 + 110011 = 111001   C = 110101

整体右移一位： A此时是补码负数，所以在空缺位置补1

 

 

 

第三步：

 

  判断C中最低两位的数 10，所以减去B，等于加上-B

 A = 111100 = 001101 = 1 001001    C = 111010

这个地方1 是超出范围的，1不计，再整体右移

这里A为补码正数，所以在空缺位置补0

 

 

第四步 

 判断C中最低两位的数，01，所以+B 

A= 000100 + 110011 = 110111  C= 111101

整体右移，然后A补1 

 

 

共四次循环，

开始校正： 此时C最低两位为10，因此要-B

A = 111011 + 001101 = 1 001000（最高位舍去）     C = 111110 ,这个时候不需要移位了

考虑到乘数C的底两位只是用来参考位判断，所以只取C的前四位

最后得 z = 001000 1111 由于最高得两位是符号判断位，所以最终

z = + 0.1000 1111