2026.1 重庆集训

Day1 网络流

P2762 太空飞行计划问题：

考虑怎么在网络上体现 \(R_i\) 的实验器材全部解锁才能实现 \(i\)。这个模型是最大权闭合子图问题，考虑这样建图：

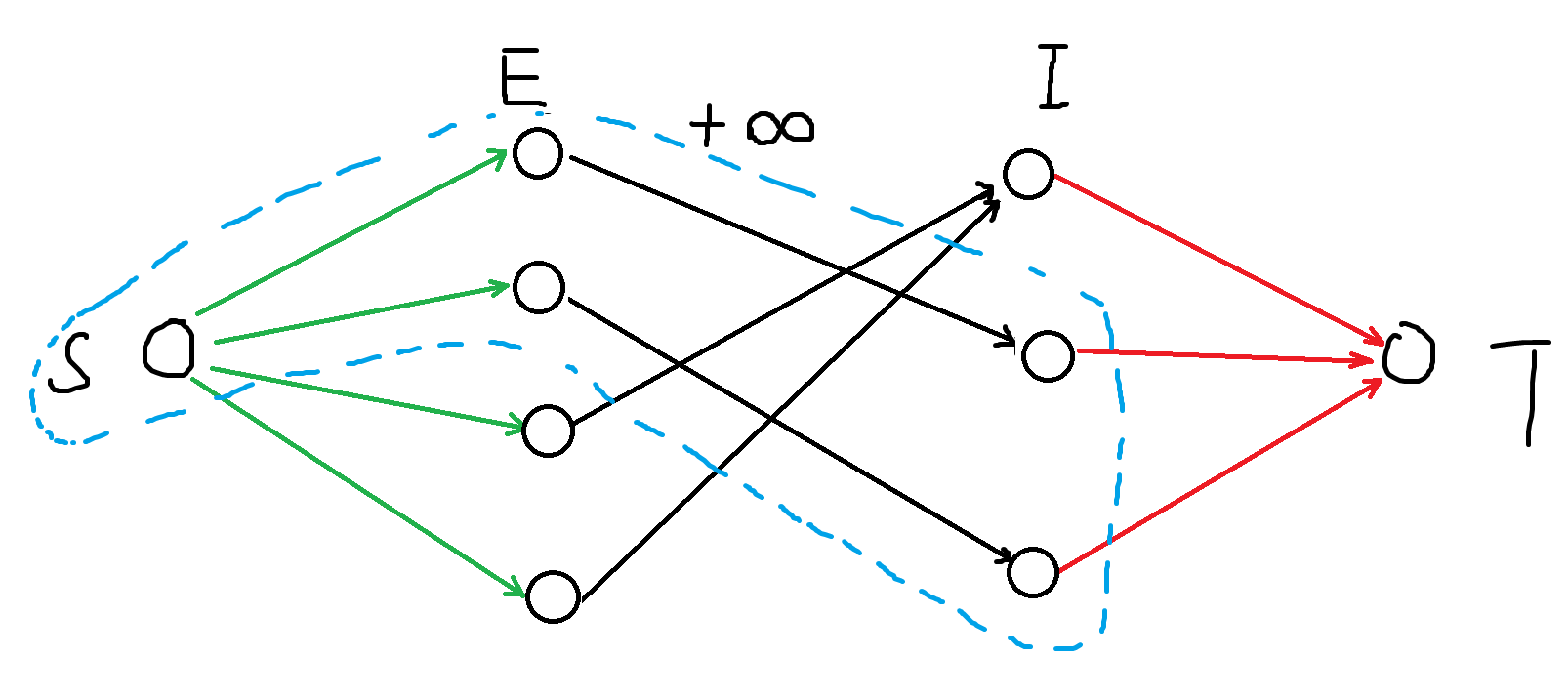
左边表示实验，右边表示器材，从 \(s\to i\) 的容量为 \(p_i\)，中间的边 \(i\to j\) 容量为 \(+\infty\)，\(j\to t\) 的容量 \(c_j\)。如果我们在这个网络 \(G\) 上跑最小割，那么我们令 \(S\) 中选择的实验和器材那么由于中间的容量被赋了 \(+\infty\)，起到了防止被割开的作用，这样保证了 \(i\) 如果要被解锁则需要购买所有 \(R_i\)。

考虑此时最小割 \(W\) 的意义，我们发现此时 \(W\) 表示 \(\min\set{ (不选择的 \sum p_i)+(选择的 -\sum c_j)}\)，那么可以发现 \((\sum p_i)-W\) 就是原问题的答案。