2025.12~2026.3 训练做题记录
数据结构1
P6617 查找 Search:可以做出简单转化,\(pre_i\) 表示上一个 \(w-a_i\) 出现的位置,则询问相当于 \(\max\limits_{i=l}^{r} pre_i\ge l\),可以在线段树上维护 \(pre\) 做到简单查询。修改较为复杂,更改 \(a_x\) 会导致后面某些 \(w-a_x\) 依赖于 \(a_x\) 的位置,直接暴力遍历这些点重新着前驱显然是不行的,不过重新考虑我们的目标,我们并不需要每时每刻都维护完全正确的 \(pre\),考虑这样一个结构:\({\color{red}\bullet}{\color{green}\bullet}{\color{green}\bullet}\),两个绿色点依赖于红色点,则不难发现可以直接将后面的位置 \(pre\) 设成 \(0\),这样是不影响答案的,更一般的,\(x<p_1<p_2< \dots< p_k\),其中 \(p_{1\sim k}\) 是依赖于 \(a_x\) 的位置,则可以 \(p_{2\sim k}\) 都赋成 \(0\),只有 \(p_1\) 维护正确的 \(pre\) 即可。那么这样修改时只需要单点更新即可。
P5025 [SNOI2017] 炸弹:线段树优化建图。可以图论建模,\(i\) 向 \([x_i-r_i,x_i+r_i]\) 内的点连边,考虑优化建图,在序列上建立线段树,对于点 \(u\),如果可以到点 \(u\) 对应的区间则一定可以到 \(lc,rc\),因此 \(u\to lc, u\to rc\) 连边。然后对于 \(i\) 向 \([l,r]\) 内的所有位置连边,可以将所有最靠上的区间覆盖掉,向儿子的边可以看作自动下传了这些边的可达关系。这样就可以只连 \(O(n\log n)\) 条边,之后的问题就是有向图上的可达点,先tarjan缩点,然后跑拓扑,此处可以用性质,即每个点最终可以走到的一定是一个区间,因此直接求出能到的点的最小和最大编号即可。
P7357 「PMOI-1」中位数:主席树妙用。独立想到的:考虑二分中位数,那么答案 \(\ge x\) 等价于 \(g(x)=\sum [a_i\ge x]-\sum [a_i<x]\ge 0\),于是要最大化路径上 \(g(x)\) 的值。拆贡献,若一个点 \(a_i<x\) 则权值视为 \(-1\),否则权值视为 \(1\),令 \(d_u\) 表示 \(u\) 到根的权值和,主要任务就是要分别在 \(u\) 子树和 \(v\) 子树内找到最大的 \(x,y\) 使得其 \(d\) 的值最大。考虑在值域的前缀上建立主席树,具体的,对于 \(rt_{x^{\prime}}\) 这棵树,我们维护 \(x=x^{\prime}\) 时每个点的 \(d\) 值,当然要映射到 \(\mathrm{dfn}\) 上方便查询和修改。其可行性在于每次 \(x\) 增加时可以直接通过找到变化的点更新变化量做到,是区间加,再维护区间最大值在查一下子树即可快速得到 \(d_x,d_y\)。考虑修改怎么做,这个 \(\oplus 1\) 的性质肯定要用上,这以为着每次修改只是形如 \(x\to x-1\) 或 \(x\to x+1\),那么我们发现在前缀上只会影响一个位置的值,直接更改即可。时间复杂度 \(O(q\log^2 n)\)。
基础优化技巧1
P3350 [ZJOI2016] 旅行者:二维分治。对于多组询问考虑二维平面上的分治,用 \(\mathrm{solve}(lx,rx,ly,ry,Q)\) 表示处理 \([lx,rx][ly,ry]\) 的子矩阵,其中要处理的询问集合为 \(Q\)。分治自然需要取一个分界点,此时按照 \(x\) 分割和按照 \(y\) 分割都可以,先考虑按 \(y\) 轴割开,即用一条水平线 \(mid=\frac{ly+ry}{2}\) 分开询问,那么对于跨过 \(mid\) 的询问,其一定会经过 \(y=mid\) 这条分割线,而没有跨过的也可以经过这条线绕过去,因此遍历这条分界线上的点然后跑最短路,将两点的 \(dis\) 拼起来就可以更新这条询问的答案,然后继续分治下去即可,不难发现这样一定可以覆盖所有决策。不过此时我们发现需要遍历分界线上的每个点跑,因此要尽量让分界线上的点尽可能少,因此 \(x,y\) 中应选择分割线较短的一个进行分割。这样的复杂度看似很暴力,分析一下时间复杂度,直接对第一层分治分析,记 \(S=nm\),那么分割线的长度最大只会是 \(\sqrt{S}\),主定理分析时间复杂度就是 \(O(S\sqrt{S}\log S)\)。
P2597 [ZJOI2012] 灾难:很妙的图论建模题。原DAG显然很不适合体现这个“灭绝”的关系,考虑想办法建出一棵灭绝树,其满足 \(u\) 会灭绝则 \(u\) 的子树中的所有点都会灭绝,也即这棵树满足若 \(fa_u\) 灭绝则 \(u\) 会灭绝。如果我们可以构造出这棵树则每个点的答案就是子树大小。考虑怎么构造这棵树,对于原DAG的某个点 \(u\),其灭绝依赖于其入点,假设其入点为 \(v_1,v_2,\dots,v_k\to u\),则 \(u\) 灭绝当且仅当 \(v_{1\sim k}\) 全部都灭绝,\(v_{1\sim k}\) 都灭绝意味着什么?根据我们这棵树的定义,这个条件等价于 \(\mathrm{LCA}=\mathrm{lca}(v_1,v_2,\dots,v_k)\) 会灭绝,因此我们在这棵树上可以连出边 \(\mathrm{LCA}\to u\),如图:
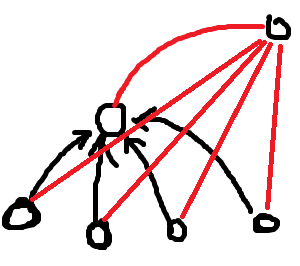
那么应该按什么顺序构造?我们发现如果对 \(u\) 连边时要求 \(v_{1\sim k}\) 都已经加入树中,因此直接按照拓扑序构造就是正确的!时间复杂度 \(O(n\log n)\)。
P6623 [省选联考 2020 A 卷] 树:一个比较显然的想法就是用 \(\texttt{Trie}\) 树存下子树中的 \((w_x+dis)\),于是我们需要支持三种操作:插入一个数、给目前 \(\texttt{Trie}\) 中的所有数 \(+1\),合并两棵 \(\texttt{Trie}\)。其中插入和合并的操作都是简单的,考虑全局 \(+1\) 怎么做,考虑其意义就是将这个数末尾一段极长的 \(1\) 推成 \(0\) 然后把更高位的 \(0\) 改成 \(1\)。由于这个操作是从低位到高位的一个进位过程,考虑将所有数倒着插入,即从低往高位插入数,记给 \(u\) 子树中的数加 \(+1\) 的操作为 \(inc(u)\),则 \(+1\) 后这一位会 \(0\to 1,1\to 0\),所以先交换左右子树,然后对于 \(1\to 0\) 其会对更高位进位,相当于在更高位作用一个 \(+1\),因此递归到 \(inc(ch_{u,0})\) 即可,这样只会走一边,时间复杂度是 \(O(\log V)\)。
动态规划1
P4590 [TJOI2018] 游园会:dp套dp,由于 \(B\) 串的长度只有最多 \(15\),因此在LCS的dp中有信息 \(dp_{i,1},dp_{i,2},\dots,dp_{i,K}\),但是把这些全部放进状态里是不现实的,这样具有 \(O(K^K)\) 的信息,挖掘一下性质,考虑相邻两项的差分,我们有 \(dp_{i,j}-dp_{i,j-1}=0/1\),因为转移时增量最多为 \(1\),因此可以存下 \(dp_i\) 的差分数组,这个 \(0/1\) 序列可以 \(O(2^K)\) 表示,再存一维表示匹配到哪一位,时间复杂度 \(O(n2^KK|\Sigma|^2)\),可以通过。
P7519 [省选联考 2021 A/B 卷] 滚榜:状压dp。可以考虑到一个很人机的dp,\(f(S,u,i,j)\) 表示前 \(k=|S|\) 个位置填的状态为 \(S\),且 \(p_k=u\),\(b_k=i,\sum b=j\) 的方案数,这样状态数已经达到了 \(O(2^nnm^2)\) 无法接受。重新审视一下条件,某一种排名 \(p\) 合法则只需要有一种能够使其合法的 \(b\),尝试贪心地构造最优的 \(b\),我们发现由于最后 \(p_n\) 一定会登顶,所以 \(b_n\) 是可以任意大的,也就是我们可以让 \(b_{1\sim n-1}\) 尽可能的小,然后最后用 \(b_n\) 将其上调到 \(m\),如果可以做到则合法。分析一下,要有 \(a_{p_i}+b_i\ge(>) a_{p_{i-1}}+b_{i-1}\),也即 \(b_i\) 最小取到 \(\max(b_{i-1},a_{p_{i-1}}-a_{p_i}+b_{i-1}+[p_i>p_{i-1}])\),我们发现 \(b_i\) 与 \(b_{i-1}\) 联系密切,考虑 \(b_i-b_{i-1}\) 的值,我们发现 \(b_i-b_{i-1}=\max(0,a_{p_{i-1}}-a_{p_i}+[p_i>p_{i-1}])\),这意味着我们可以拆贡献计算了,记 \(\Delta_i=b_i-b_{i-1}\),则 \(\sum b=\sum \Delta_i(n-i)\),因此我们只需要在dp时表示出 \(\sum b\) 即可,因此缩减到 \(f(S,i,j)\) 的状态,时间复杂度为 \(O(2^n n^2m)\),可以通过。
P5249 [LnOI2019] 加特林轮盘赌:深深地感受到自己的弱小。考虑怎样可以表示出目前的某个局面,假设现在有 \(i\) 个人剩下,考虑随便钦定一个顺序按顺时针编号:\(1,2,\dots,j,\dots,i\),并假设枪口对着 \(1\) 号点,考察 \(j\) 号点的胜率,记这个胜率为 \(f(i,j)\),可以发现什么?考虑用第 \(1\) 个人的死亡与否来划分状态,如果 \(1\) 号点被毙掉了,则相当于毙一个然后转一位,这等价于 \(f(i-1,j-1)\),因此我们可以得出转移式为 \(f(i,j)=P_0\cdot f(i-1,j-1)+(1-P_0)\cdot f(i,j-1)\),当然这个是对 \(j\ge 2\) 成立的,同时,我们还可以挖掘到一个等式:\(\sum f(i,j)=1\)。综合一下,则上述所有条件可以表示成如下形式:
那么我们总共得到了 \(n\) 个等式,直接高斯消元可以做到 \(O(n^3)\) 解出所有 \(x_j\),无法接受。但是注意到这个形式很特殊,我们可以简单的将所有 \(\textcircled{1}\) 带入 \(\textcircled{2}\),得到
因此我们可以直接表示成 \(Kx_1+B=1\) 的形式,那么 \(x_1\) 可以被解出来,那么其他的项也就解决了,不难发现系数和带回都可以 \(O(n)\) 解决,因此时间复杂度 \(O(n^2)\)。
基础优化技巧2
P9067 [Ynoi Easy Round 2022] 虚空处刑 TEST_105:启发式合并。这个极大连通块代表的就是在树上的极大同色连通块。考虑使用并查集维护连通块,并且每个点 \(x\) 指向的是其所在的连通块中最高的那个点,现在默认用这个代表元代表这个连通块。对于 \(x\) 连通块,其可以看作下图的形态:
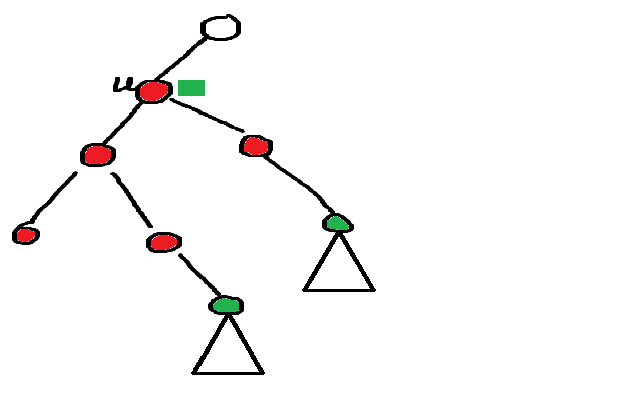
如果我们将 \(x\) 所在的连通块全部改成绿色,则这个连通块会接上下面的绿色子树形成更大的一个连通块,考虑维护一个 map<int,list<int> > mp[N];,其中 \(mp_{x,c}\) 表示点 \(x\) 连通块往下紧接着的颜色为 \(c\) 的连通块代表元,用一个 list<int> 存,这样可以做到 \(O(1)\) 合并 x.splice(x.end(),y)。对 \(x\) 连通块染成绿色 \(c\) 时,暴力遍历 \(mp_{x,c}\) 中的点 \(y\),将 \(mp_y\) 启发式合并 到 \(mp_x\) 中。但是这样只能维护子树中的连通信息,对于 \(fa_x\) 还需要更改,如果 \(fa\) 也是绿色则将 \(x\) 的信息合并上去,否则 \(x\) 将作为 \(fa_x\) 的一个附属子树存在,在 \(mp_{fa_x,c}\) 中加入 \(x\) 即可。
分析一下时间复杂度,由于每次合并的集合不交并且运用了启发式合并,所以时间复杂度是 \(O(n\log n)\)。
P8421 [THUPC 2022 决赛] rsraogps:扫描线+增量维护。很巧妙的题,首先想办法处理计算 \(\forall [l^\prime,r^\prime]\subseteq [l,r]\) 的所有贡献,考虑扫描线,扫描到 \(r\) 时处理出 \(s_i\) 表示所有 \(l^\prime\le i,r^\prime\le r\) 的贡献,即扫到的区间中左端点在 \(i\) 及其左侧的贡献和,那么这样挂在 \(r\) 上的询问可以直接 \(s_r-s_{l-1}\) 得到。观察一下 \(\wedge,\vee,\gcd\),这三个运算符有很经典的性质就是往前扫的时候最多变化 \(O(\log V)\) 次,考虑往右走到 \(r\) 时动态地维护 \([i,r]\) 的 \(a,b,c\) 值,记这个集合为 \(S(i,r)\),我们发现如果找到一个最大的 \(p\) 使得 \(\forall i\in[p+1,r],S(i,r)\ne S(i,r-1)\),即 \([1,p]\) 中的所有 \(a,b,c\) 都和 \(r-1\) 时的一样不会改变,而 \([p+1,r]\) 中的会发生改变,考虑直接暴力往前找 \(p\),可以发现此时最多只会走 \(O(\log V)\) 次就会停下,因为三个运算符都只会最多变 \(O(\log V)\) 次,固 \(O(\log V)\) 次之后所有值都不会再改变。那么我们可以直接暴力遍历 \([p+1,r]\) 对贡献做出更改,而 \([1,p]\) 的部分和 \(r-1\) 时的贡献是一样的。对于 \([1,p]\) 其增量 \(\Delta_i=\Delta_i^\prime\),考虑维护 \(t_i\) 表示位置 \(i\) 上一次被暴力更改的时间戳,同时维护当前时间戳 \(T\),类似历史和的思想。并维护 \(prv_i\) 表示 \(i\) 已经被加上的贡献,则 \(s_i=prv_i+\delta_i(T-t_i)\),这样更改时只需要处理 \([p+1,r]\) 部分,暴力改掉即可。时间复杂度 \(O(n\log n)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号