基本树

1. 什么是树

树是一种特殊的图，它是一种 $n$ 个点，$n-1$ 条边，没有环和重边的一种特殊的图。你可以将它倒过来看。
生活中的树：

图中的树：

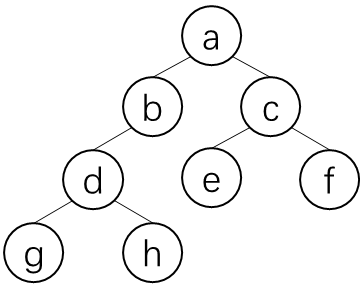
2. 有根树、无根树

一个没有固定根结点的树称为无根树；在无根树的基础上，指定一个结点称为根，则形成一棵有根树。一般来说，我们用 $1$ 来表示无根树的根。

3. 一些其他的树

• 森林：每个连通块都是树的图。按照定义，一棵树也是森林。
• 生成树：一个连通无向图的生成子图，同时要求是树。也即在图的边集中选择 $n-1$ 条，将所有顶点连通。

4. 树的组成

• 父亲：对于除根以外的每个结点，定义为从该结点到根路径上的第二个结点。根结点没有父结点。
• 祖先：一个结点到根结点的路径上，除了它本身外的结点。
• 子结点：如果 $u$ 是 $v$ 的父亲，那么 $v$ 是 $u$ 的子结点。
• 叶子：只有父亲的子结点
• 结点的深度：到根结点的路径上的边数。
• 树的高度：所有结点的深度的最大值。

5. 一些特殊的树

• 链：满足与任一结点相连的边不超过 $2$ 条的树称为链。
• 菊花图：满足存在 $u$ 使得所有除 $u$ 以外结点均与 $u$ 相连的树称为菊花图。
• 二叉树：$k$ 叉树的每个节点的孩子数量不超过 $k$。二叉树即每个节点的孩子数量不超过 $k$。
• 完全二叉树：只有最下面两层结点的度数可以小于 $2$，且最下面一层的结点都集中在该层最左边的连续位置上。
• 完美二叉树：所有叶结点的深度均相同的二叉树称为完美二叉树。完美二叉树有 $1+2+4+8+\cdots+2^k=2^{k+1}-1$ 个节点。其中 $k$ 为树的高度。

6. 二叉树的存储

• 二叉树——数组存储法
  如果给一棵完全二叉树从左往右、从上往下标号，那么 $i$ 号节点的父亲编号为 $\lfloor \dfrac{i}{2} \rfloor$，左儿子编号为 $2i$，右儿子编号为 $2i+1$。
  那么我们可以用一个数组 a[i] 来存储一颗二叉树
  注意，这种方法最多需要开 $2^n$ 个节点。
• 二叉树——记录节点法
  开三个数组：parent[i]、lchild[i]、rchild[i]，分别记录 $i$ 号节点的父亲、左孩子、右孩子。

7. $k$ 叉树的存储

由于树是特殊的图，所以我们可以用邻接表来存一棵树。具体存法详见基本图论的第 $7$ 节。
这下有人就要问了，为什么不用邻接矩阵？
邻接矩阵存稀疏图太浪费空间，而树只有 $n-1$ 条边，肯定是一张稀疏图。
对于一些特殊的题目，只需要存父亲。

8. 树上DFS

树上DFS模板：

void dfs(int x,int last)
{
        for(int i=0;i<a[i].size();i++)
        {
            int u=a[x][i];
            if(u==last) continue;
            ...
            dfs(u,x);
            ...
        }
}

接下来分析一下：

• $\text x$：表示当前DFS遍历的编号
• $\text{last}$：$\text x$ 的父亲节点
• $\text u$：$\text x$ 的一个儿子
• if(u==last) continue：当遍历到父亲时，立刻跳过。如果是叶子节点，相当于什么也没做
• dfs(u,x)：搜索

9. 树上BFS

树上BFS模板：

struct node{
	    int x,last;
};
...
q.push(node{根节点编号,-1});
while(!q.empty())
{
        node u=q.front();q.pop();
        ...
        for(int i=0;i<a[u.x].size();i++)
        {
            int v=a[u.x][i];
            if(u.last==v) continue;
            ...
            q.push({v,u.last});
            ...
        }
        ...
}

同理：

• $\text{u.x}$：当前点的编号
• $\text{u.last}$：$\text{u.x}$ 的父亲
• $\text{v}$：$\text{u.x}$ 的一个儿子

10. 二叉树的遍历

• 二叉树的三种遍历
  二叉树的遍历分别为先序遍历、中序遍历、后序遍历。“左”代表的是左边的孩子，“右”代表的是右边的孩子
  • 先序遍历
    按照根、左、右的顺序来遍历
  • 中序遍历
    按照左、根、右的顺序来遍历
  • 后序遍历
    按照左、右、根的顺序来遍历
• 通过两种遍历求出另一种遍历
  例：已知一棵树中序遍历为CBADEFGH。
  前序遍历为ABEDFCHG。
  那么根节点为A（前序遍历首字母）
  那么这棵树中序遍历就变成了：CB|A|DEFGH，根据左根右的顺序，左子树由CB组成，右子树由 DEFGH组成，后序遍历就应该为 xxxxxxA。接下来递归计算便可。
  注意：通过先序遍历和后序遍历无法计算出中序遍历，详见洛谷P1229
• 一些模板代码
  1. 三种遍历代码（这里使用记录节点法）
     • 先序遍历

     void xian(int x)
     {
             cout<<x<<" ";
             if(lchild[x]) xian(lchild[x]);
             if(rchild[x]) xian(rchild[x]);
     }

     • 中序遍历

     void zhong(int x)
     {
             if(lchild[x]) zhong(lchild[x]);
             cout<<x<<" ";
             if(rchild[x]) zhong(rchild[x]);
     }

     • 后序遍历

     void hou(int x)
     {
             if(lchild[x]) hou(lchild[x]);
             if(rchild[x]) hou(rchild[x]);
             cout<<x<<" ";
     }

  2. 已知中序和先序/后序遍历，求另外一种遍历
     • 已知先序、中序
       例题
       AC记录
     • 已知后序、中序
       例题
       AC记录