基础dp

1. 什么是dp

动态规划是一种求最优化问题的算法。
dp有三个性质：重叠子问题、无后效性、最优子结构性质
至于什么意思，例题中再告诉你

2. dp例题 $1$：数字三角形

• 解法一：搜索
  这题最容易、最好写的办法为搜索。
  不废话，直接上核心代码：

int dfs(int x,int y)
{
         if(x==n) return a[x][y];
         return max(dfs(x+1,y),dfs(x+1,y+1))+a[x][y];
}

dfs(x,y)的意思看都看得出来；$(x+1,y)$ 和 $(x+1,y+1)$ 的位置，表示正下方的格子和右下方的格子；if(x==n)是递归边界。
这个算法的时间复杂度为 $O(2^{(n^2)})=O(2^n)$，因为每次都要分成两条路去算。

• 解法二：记忆化
  计算时有许多亢余，例如计算两个黑色三角形时，重复计算了红色三角形：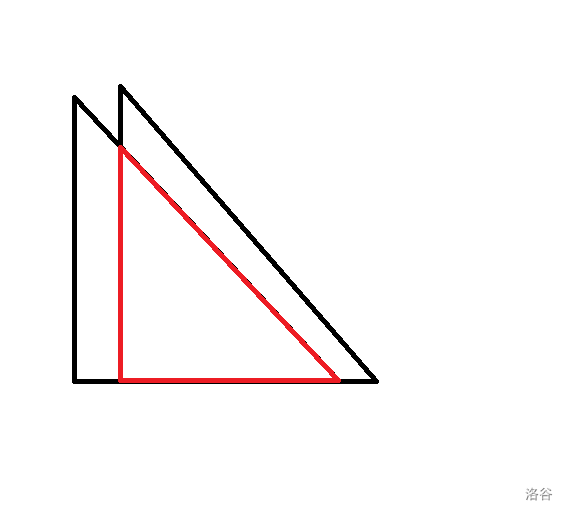
  那么开一个f[x][y]数组，记录这个节点的为起点的答案。
  核心代码：

int dfs(int x,int y)
{
         if(x==n) return a[x][y];
         if(f[x][y]) return f[x][y];
         f[x][y]=max(dfs(x+1,y),dfs(x+1,y+1))+a[x][y];
         return f[x][y];
}

时间复杂度 $O(n^2)$

• 解法三：递推
  我们从上往下推，还可以从下往上推。
  代码很好实现：

for(int i=1;i<=n;i++)
         dp[n][i]=a[n][i];
 for(int i=n-1;i>=1;i--)
 	      for(int j=1;j<=n;j++)
 	          dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+a[i][j];

好消息：这就是dp
$dp_{i,j}$ 表示以这个节点的为起点的答案。
重叠子问题：就像红色的三角形一样的重复的问题
无后效性：像这个题，不可能从上面的点反而转向下面，可以理解为DAG
最优子结构：这个题可以通过下面的点求出上面的点的答案，最优子结构是指可以通过子问题的最优解求出最优解的题。
像 $dp_{i,j}$ 这种，叫做状态。
像 $dp_{i,j}=\max(dp_{i+1,j},dp_{i+1,j+1})+a_{i,j}$ 这种转移的方程，叫做状态转移方程，这个过程叫做转移。

3. dp例题 $2$：硬币问题

• 解法一：贪心
  这题和生活中问题付钱很像。一般来说，我们会先选面值大多的钱。
  但是这道题有反例（样例一）：$15$；如果先选 $11$，需要 $5$ 张（$\{11,1,1,1,1\}$），不是最优解。
• 解法二：搜索
  贪心不行，那就暴力解！！！
  代码很容易写出：

int dfs(int x)
{
        if(x==1||x==5||x==11) return 1;
        return f[x]=( min(dfs(x-1), min(x-5,x-11) ) );
}

又有重复计算，记忆化！！！

int dfs(int x)
{
        if(f[x]) return f[x];
        if(x==1||x==5||x==11) return f[x]=1;
        return f[x]=( min(dfs(x-1), min(x-5,x-11) ) )+1;
}

• 解法三：DP
  dfs设的状态为“$x$ 元至少要付的钱的张数”。
  $dp_i$ 的定义一样。
  转移方程：为 $dp_i=\min\{dp_{i-1},dp_{i-5},dp_{i-11}\}+1$ 意义为上一次选 $1$ 元/ $5$ 元/ $11$ 元的最优解。
  代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
int dp[1000001]={0,1,2,3,4,1,2,3,4,5,2,1};
signed main()
{
        int n;
        cin>>n;
        for(int i=12;i<=n;i++)
            dp[i]=min(dp[i-11]+1,min(dp[i-5]+1,dp[i-1]+1));
        cout<<dp[n];
        return 0;
}

注意dp的的一个重点：记得赋初值。如上题初值为底层的答案都为自己、本题前 $11$ 个答案必须提前计算。

4. dp例题 $3$：文字工作

状态：$dp_i$ 表示打 $i$ 个字的最优解
方程：$dp_i$ 要不从前一半转移，要不直接打一个字。注意奇数项不能除 $2$。即： $dp_i=\begin{cases} dp_i=dp_{i-1}+1\\ dp_i=dp_\frac{{i}}{2}&i\bmod 2=0 \end{cases}$

5. dp、记忆化搜索：滑雪

这题一看，我敢打赌绝对有想DP的人
然而第一眼，似乎也想不出方程
DP可以解，但是要先给所有边排序，给所有点DP，DP方程很简单。可能还需要一点点的 prtority_queue……
你再用记忆化搜索：$\color{blue}\text水$ 题啊！！！
只需要写一点点长的判断就行了。给大家偷个懒，判断代码：nx<=n&&ny<=m&&nx>=1&&ny>=1&&a[nx][ny]<a[x][y]，nx、ny表示下一个划的点。 然后发现你挂了（不会有人复制了吧）
$\color{#00B8D4} \rule{2pt}{44pt} \color{#E5F8FB} \rule[24pt]{200pt}{20pt} \color{#e8e8e8}\rule{0.5pt}{44pt} \color{#f5f5f5}\rule{0.5pt}{44pt} \color{#fafafa}\rule{0.5pt}{44pt} \kern{-200pt}\kern{-1.5pt} \color{#bfbfbf}\rule[0pt]{200pt}{0pt}\kern{-200pt} \color{#d6d6d6}\rule[-0.5pt]{200pt}{0pt}\kern{-200pt} \color{#ececec}\rule[-1pt]{200pt}{0pt}\kern{-200pt} \color{#f8f8f8}\rule[-1.5pt]{200pt}{0pt}\kern{-200pt} \color{black} \raisebox{24pt}{ \raisebox{6pt}{ \kern{-1pt} \color{#00B8D4}\large{\kern{2pt}\bf{i}\kern{5.5pt}} \raisebox{1.5pt}{ \color{#404040}\footnotesize \kern{-4pt}\sf\bf{提醒} }}}\kern{-200pt}$. $\kern{0pt}\raisebox{10pt}{\footnotesize\sf{ 题目不一定要用dp，使用最简单的方法才能ak IOI}}$

6. 推荐练习

• 最长不降子序列
• 挖地雷
• 乌龟棋
• 一个很可爱而恐怖的题单