树状数组

1. $\text{lowbit}(n)$

先介绍一个函数：$\text{lowbit}(n)$。它表示二进制下从右起第一个 $1$ 的位置表示的数。例如：$(114514)_{10}=(11011111101010010)_2$，故 $\text{lowbit}(114514)=2^2=4$。有 $\text{lowbit}(k)=\text{k\&(-k)}$

2. 树状数组例题 $1$：【模板】树状数组 1

容易想到两种方法：

• 暴力
  暴力修改每个数，每次暴力求和。
• 前缀和
  每次修改 $s_i(s_i=\sum\limits_{j=1}^ia_j)$，每次快速求和。

他们时间复杂度分别如下：

方法	修改	查询
暴力	$O(1)$	$O(n)$
前缀和	$O(n)$	$O(1)$

肯定都无法通过。考虑使用树状数组。
定义 $c_i=\sum\limits^i_{j=i-\text{lowbit}(n)}a_j$。画个图就是这样：

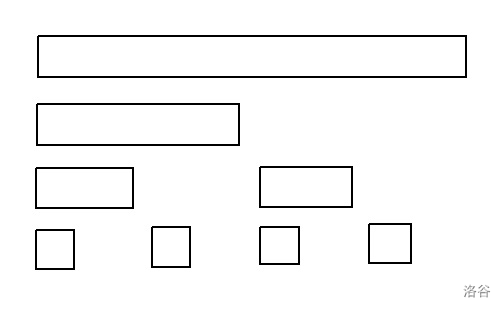
这样子，便可以看到所有 $1\sim i$ 的区间可以组合出来。这样就可以使用前缀和快速计算了。
现在的问题是：怎样快速维护 $c_i$、求 $s_i$。

• 维护 $c_i$
  假设修改一个值 $a_i$，那么会需要改许多 $c$。具体是哪些呢？首先，$c_i$ 是肯定有的。然后修改 $c_{i+\text{lowbit}(i)}$，然后继续修改便可。代码如下：

void add(int x,int k)
 {
  	while(x<=n)
  	{
  		tr[x]+=k;
  		x+=lowbit(x);
  	}
 }

• 求 $s_i$
  要求的是 $s_i$，$s_i=c_i+s_{i-\text{lowbit}(i)}$（易得）。故可以一直循环下去。代码如下：

int sum(int x)
{
 	int ans=0;
 	while(x!=0)
 	{
 		ans+=tr[x];
 		x-=lowbit(x);
 	}
 	return ans;
}

完整代码如下：

#include<bits/stdc++.h>
#define int long long
#define lowbit(x) (x&(-x))
using namespace std;
int tr[500006];
int n,m;
void add(int x,int k)
{
		while(x<=n)
		{
			tr[x]+=k;
			x+=lowbit(x);
		}
}
int sum(int x)
{
		int ans=0;
		while(x!=0)
		{
			ans+=tr[x];
			x-=lowbit(x);
		}
		return ans;
}
signed main()
{
      cin>>n>>m;
      for(int i=1;i<=n;i++)
      {
          int a;
          cin>>a;
          add(i,a);
      }
      while(m--)
      {
          int op,a,b;
          cin>>op>>a>>b;
          if(op==1) add(a,b);
          else cout<<sum(b)-sum(a-1)<<endl;
      }
      return 0;
}

3. 树状数组例题 $2$：【模板】树状数组 2

记 $b_i=a_i-a_{i-1}$（即差分），则修改时，只需要修改 $l,r+1$ 上的位置便可。
代码如下：

#include<bits/stdc++.h>
#define int long long
#define lowbit(x) (x&(-x))
using namespace std;
int tr[500006];
int s[500006];
int n,m;
void add(int x,int k)
{
      while(x<=n)
      {
          tr[x]+=k;
          x+=lowbit(x);
      }
}
int sum(int x)
{
      int ans=0;
      while(x!=0)
      {
          ans+=tr[x];
          x-=lowbit(x);
      }
      return ans;
}
signed main()
{
      cin>>n>>m;
      for(int i=1;i<=n;i++) cin>>s[i];
      while(m--)
      {
          int op,a,b,c;
          cin>>op>>a;
          if(op==1)
          {
              cin>>b>>c;
              add(a,c);
              add(b+1,-c);
          }
          else
          {
              cout<<s[a]+sum(a)<<endl;
          }
      }
      return 0;
}

4. 树状数组例题 $3$：Preprefix sum

这里牵涉到了单点查询和超级区间修改，不考虑树状数组。
先看一下要求的问题：求 $SS_i=\sum\limits^{n}_{i=1} \sum\limits^{i}_{j=1} a_j$。
展开看一下：

$$n=1,SS_i=a_1$$ $$n=2,SS_i=a_1+(a_1+a_2)$$ $$n=3,SS_i=a_1+(a_1+a_2)+(a_1+a_2+a_3)$$

归纳一下：$SS_i=\sum\limits^n_{i=1} (n-i+1)a_i$。提一下柿子：$(n+1)\sum a_i+\sum (i\times a_i)$。
由于这两个柿子都能用树状数组维护，所以可以用树状数组来维护查询和修改。
修改代码：

add1(x,y-a[x]);add2(x,(y-a[x])*x);

查询代码：

ans=((x+1)*ask1(x)-ask2(x));