搜索

1. 启动发式搜索：A*

例题：八数码难题
什么是A*呢？举个例子，怎么算从长沙到北京的最短路。
假设有两个点 $A,B$，我们可以优先选择直线距离短的点，先算到那里的点。
也就是，计算一个估计值。在A*中，我们称作 $h$*$(x)$。
A*有一个很重要的等式：$f$*$(x)=g(x)+h$*$(x)$。我们分别来解释一下：

• $h$*$(x)$：估计值，表示预计要怎么样。
• $g(x)$：已走值，表示已经走了多少。
• $f$*$(x)$：估值函数，表示从起点到终点预计的值。

但估计值不能乱写，必须满足“估计值 $\le$ 实际值”。
A*实现很简单，就是简单的BFS。难在怎么设计估值函数。
估值函数中，$g(x)$ 是确定的，所以要让 $h$*$(x)$ 尽量小。
例如八数码难题中，我们可以设计与目标状态不同的位置总数为 $h$*$(x)$。
代码实现如下：

int h(string s)
{
	int ans=0;
	for(int i=1;i<=9;i++)
		if(s[i]!=End[i])
			ans++;
	return ans;
}

实际上，如果想要速度更快，可以将估值函数改成：$f$*$(x)=g(x)+h$*$(x)\times k$，$k$ 越大，速度越快，但可能出现错误的答案；$k=0$，就变成了普通BFS。如这题，$k=1.8$，就会WA掉几个点。

---

后记：

Q：为什么 $k$ 越大，会出现错误答案？

A：原因有二：

1. $k$ 越大，就更可能超过预计值
2. 因为这是启动式搜索，$k$ 大会炸掉（可莉：？）。

2. 双向广搜

也称双向BFS。
什么意思呢？每次从起点和终点开始搜索。为了平衡，可以从状态数少的一边搜索。

3. 迭代加深搜索

Q：DFS有缺点吗？
A：有，可能出现一去不复返的情况。

什么意思呢？就是说，搜啊搜，搜不完。
解决方法就是迭代加深搜索
先来回顾一般的DFS：

int dfs(int x)

迭代加深的DFS是

int dfs(int x,int t)

$t$ 是什么呢？表示深度，即搜了多少次就不搜了。
主函数的搜索也就变成了这个样子：

for(int t=0;搜索成功;t++)
{
	dfs(?,t);
}

其中?为给定的值。
有些人就会嘲讽SLMXF：这不会重复计算吗？
这里举个例子，每次拓展出两个状态：
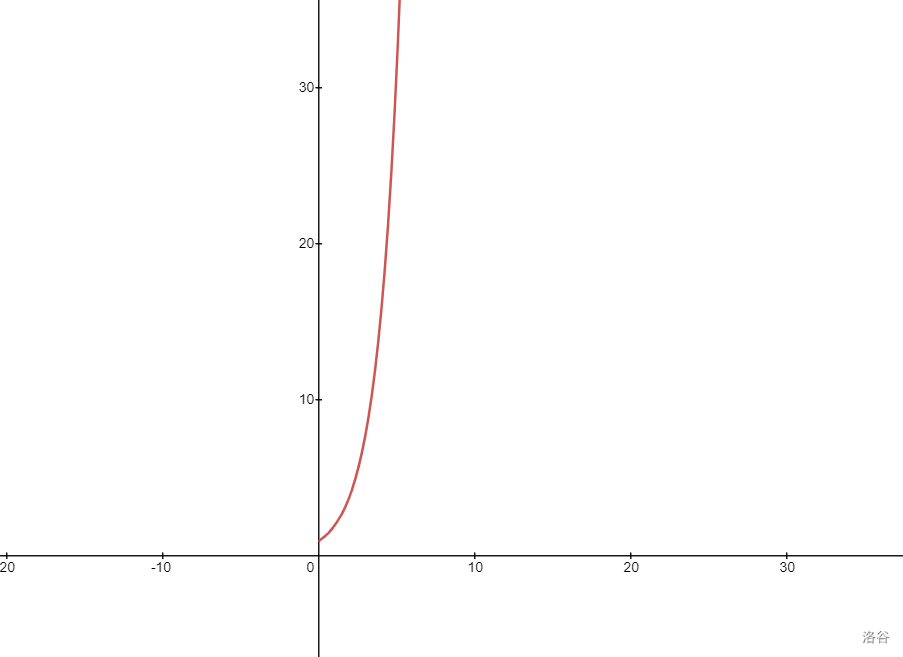
这是它的函数图像，我们发现，前面搜索过的更后一次一比，简直不值一提。
也可以证明一下：$1+2^1+2^2+\cdots+2^{n-1}<2^n$。
证明：左边是个等比数列，所以左边等于 $2^n-1$，必定有 $2^n-1<2^n$。所以他的时间复杂度可以粗略看成 $O(2^x)$。