线段树

0. 前置芝士：二叉树的存储。

如果给一棵完全二叉树从左往右、从上往下标号，那么 $i$ 号节点的父亲编号为 $\lfloor \dfrac{i}{2} \rfloor$，左儿子编号为 $2i$，右儿子编号为 $2i+1$。
那么我们可以用一个数组 a[i] 来存储一颗二叉树
注意，这种方法最多需要开 $2^n$ 个节点。线段树中为 $4n$。

删改自blog基本树

1. 线段树例题1：【模板】线段树

线段树的本质：将若干个区间用树上结点表示。
例如区间 $[l,r]$，我们记 $mid=\left \lfloor \dfrac{l+r}{2}\right \rfloor$，将 $[l,mid]$、$[mid+1,r]$ 作为它的左右儿子。
例如一张长度为 $10$ 的序列，存储下来像这样：

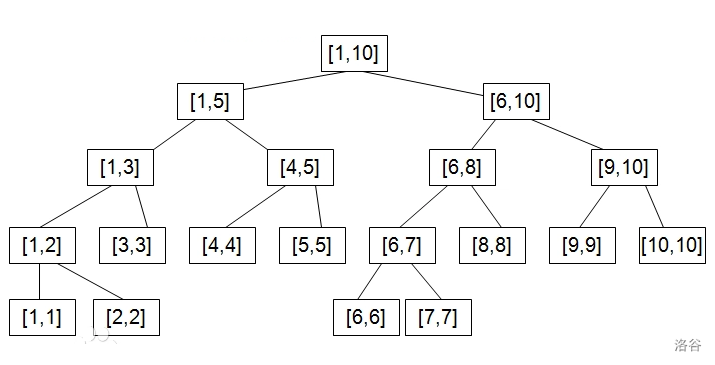
线段树有以下性质：

• 一个节点，要不有两个子节点，要不没有子节点。

• 一个线段树有 $2n-1$ 个结点。

• 一个线段树高 $\log n$。
  线段树需要满足可合并性。例如：$\max(l\sim r)=\max\{\max(l \sim x),\max(x \sim r)\}(l\le x\le r)$。
  线段树支持下列操作：

  1. 建立线段树
     线段树是递归定义的。我们知道，若区间 $[l,r]$ 中 $l=r$，则代表是叶子结点。此时 w[u]=a[l]。否则将其分成两个部分。
     最后要记得，将两个区间汇总（pushup），即 w[u]=w[u*2]+w[u*2+1]。
     建立的代码如下：

void pushup(int u)
{
           w[u]=w[u*2]+w[u*2+1];
}
void build(int u,int l,int r)
{
           if(l==r)
           {
               w[u]=a[l];
               return;
           }
           int m=(l+r)/2;
           build(u*2,l,m),build(u*2+1,m+1,r);
           pushup(u);
}

2. 单点查询
   这个没有什么意义，所以只把代码贴在这。时间复杂度为 $O(\log n)$。

long long query1(int u,int l,int r,int p)
{
	       if(l==r) return w[u];
 	       else
	       {
	  	       int m=(l+r)/2;
		       if(m>=p) return query1(u*2,l,m,p);//左子树[ l,m ]
		       else return query1(u*2+1,m+1,r,p);//右子树[m+1,r]
	       }
}
long long update1(int u,int l,int r,int p,long long x)
{
	       if(l==r) w[u]=x;
	       else
	       {
		       int m=(l+r)/2;
		       if(m>=p) update1(u*2,l,m,p,x);//左子树[ l,m ]
		       else update1(u*2+1,m+1,r,p,x);//右子树[m+1,r]
	       }
}

Q:为什么单点查询没用？

A:因为数组也能完成，而且数组好写，时间复杂度 $O(1)$。

3. 区间查询
   我们知道查询区间为 $[l,r]$。我们可以想到，如果 $[L,R]$ 属于 $[l,r]$，则直接返回当前区间和。如果完全没有交集，可以直接返回 $0$。不然，分成两部分去查找。那么区间查询代码如下：

bool InRange(int L,int R,int l,int r)
{
	       return (l<=L)&&(R<=r);
}
bool OutofRange(int L,int R,int l,int r)
{
	       return (L>r)||(R<l);
}
long long query(int u,int L,int R,int L,int r)
{
	       if(InRange(L,R,l,r)) return w[u];
	       else if(!OutofRange(L,R,l,r))
	       {
		       int m=(L+R)/2;
		       return query(u*2,L,m,l,r)+query(u*2+1,m+1,R,l,r);
	       }
	       else return 0;
}

4. 区间修改
   这里需要引入一个叫做“懒标记”的东西（也可以叫 $\text{lazy-tag}$）。它用于记录区间修改的信息。当递归至一个完全包含的区间，可以直接打一个懒标记，记录这个区间每个都需要加上某个数，并修改它的区间和，然后这里就修改完了。当你访问到一个新节点，将懒标记下放便可。
   容易得到区间修改的代码：

void maketag(int u,int len,long long x)
{
	       lzy[u]+=x;
	       w[u]+=len*x;
}
void pushdown(int u,int l,int r)
{
	       int m=(l+r)/2;
	       maketag(u*2,m-l+1,lzy[u]);
	       maketag(u*2+1,r-m,lzy[u]);
	       lzy[u]=0;
}
void update(int u,int L,int R,int l,int r,long long x)
{
	        if(InRange(L,R,l,r)) maketag(u,R-L+1,x);
	        else if(!OutofRange(L,R,l,r))
	        {
	        	int m=(L+R)/2;
	        	pushdown(u,L,R);
	        	update(u*2,L,m,l,r,x);
	        	update(u*2+1,m+1,R,l,r,x);
	        	pushup(u);
	        }
}

注意修改 $\text{query}$ 的代码：

long long query(int u,int L,int R,int l,int r)
{
	       if(InRange(L,R,l,r)) return w[u];
	       else if(!OutofRange(L,R,l,r))
	       {
		       int m=(L+R)/2;
		       pushdown(u,L,R);
		       return query(u*2,L,m,l,r)+query(u*2+1,m+1,R,l,r);
	       }
	       else return 0;
}

接下来，换道题休息一下：

2. 线段树例题2：开关

这里很简单，区间异或就是将 $0$ 和 $1$ 互换。所以稍微变动一下 $\text{maketag}$ 函数便可：

void maketag(int u,int len,long long x)
{
		lzy[u]^=1;
		w[u]=len-w[u];
}

最后说一下线段树的使用范围：“可加性”

什么意思呢？加上 $a$，加上 $b$，相当于加上 $a+b$；乘上 $x$，乘以 $y$，相当于乘上 $x\times y$……即先做 $A$，再做 $B$，相当于一起做了 $AB$。也可以看成有结合律的运算，如 $x+a+b=x+(a+b),x\oplus a\oplus b=x\oplus (a\oplus b)$，原因就不给了，可以在懒标记中发现。

推荐练习：P1438，P1253，P3373，P1908。

3. 动态开点

如果你需要维护一个 $[1,10^9]$ 的区间，你或许会掏出离散化。但如果它强制在线呢？动态开点！

动态开点的宗旨是：要用什么点就建立什么节点。以前来说，$u$ 的两个儿子是 $2u$ 和 $2u+1$，但现在变成了 $ls,rs$。

由于每次操作的时间复杂度是 $O(\log n)$，每次操作就可能创建 $O(\log n)$ 级别的点。操作 $m$ 次后，也只会创造 $O(m\log n)$ 个节点。时间复杂度同样还是 $O(\log n)$ 一次。

?.菜单——线段树

最后的最后，你肯定很讨厌定义线段树。所以这里给一个线段树：

const int maxn=500006;//依情况修改
struct Segment{//依情况修改
	long long a[maxn],w[4*maxn],lzy[4*maxn];
	void pushup(int u)
	{
		w[u]=w[u*2]+w[u*2+1];
	}
	void build(int u=1,int l=1,int r=n)
	{
		if(l==r)
		{
			w[u]=a[l];
			return;
		}
		int m=(l+r)/2;
		build(u*2,l,m),build(u*2+1,m+1,r);
			pushup(u);
	}
	bool InRange(int L,int R,int l,int r)
	{
		return (l<=L)&&(R<=r);
	}
	bool OutofRange(int L,int R,int l,int r)
	{
		return (L>r)||(R<l);
	}
	void maketag(int u,int len,long long x)
	{
		lzy[u]+=x;
		w[u]+=len*x;
	}
	void pushdown(int u,int l,int r)
	{
		int m=(l+r)/2;
		maketag(u*2,m-l+1,lzy[u]);
		maketag(u*2+1,r-m,lzy[u]);
		lzy[u]=0;
	}
	int query(int l,int r,int u=1,int L=1,int R=n)
	{
		if(InRange(L,R,l,r)) return w[u];
		else if(!OutofRange(L,R,l,r))
		{
		  int m=(L+R)/2;
		  pushdown(u,L,R);
	  	return query(l,r,u*2,L,m)+query(l,r,u*2+1,m+1,R);
		}
		else return 0;
	}
	void update(int l,int r,long long x,int u=1,int L=1,int R=n)
	{
		if(InRange(L,R,l,r)) maketag(u,R-L+1,x);
		else if(!OutofRange(L,R,l,r))
		{
			int m=(L+R)/2;
			pushdown(u,L,R);
			update(l,r,x,u*2,L,m);
			update(l,r,x,u*2+1,m+1,R);
			pushup(u);
		}
	}
};

以上是无空格版

以下是空格版

const int maxn = 500006;
struct Segment{
	long long a[maxn],w[4*maxn],lzy[4*maxn];
	void pushup(int u){
		w[u] = w[u * 2] + w[u * 2 + 1];
	}
	void build(int u = 1, int l = 1, int r = n){
		if(l == r)
		{
			w[u] = a[l];
			return;
		}
		int m = (l + r) / 2;
		build(u * 2, l, m);
		build(u * 2 + 1, m + 1, r);
		pushup(u);
	}
	bool InRange(int L, int R, int l, int r){
		return (l <= L) && (R <= r);
	}
	bool OutofRange(int L, int R, int l, int r){
		return (L > r) || (R < l);
	}
	void maketag(int u, int len, long long x){
		lzy[u] += x;
		w[u] += len * x;
	}
	void pushdown(int u, int l, int r){
		int m = (l + r) / 2;
		maketag(u * 2, m - l + 1, lzy[u]);
		maketag(u * 2 + 1, r - m, lzy[u]);
		lzy[u] = 0;
	}
	int query(int l, int r, int u = 1, int L = 1, int R = n)
	{
		if(InRange(L, R, l, r)) return w[u];
		else if(!OutofRange(L, R, l, r)){
			int m = (L + R) / 2;
			pushdown(u, L, R);
			return query(l, r, u * 2, L, m) + query(l, r, u * 2 + 1, m + 1, R);
		}
		else return 0;
	}
	void update(int l, int r, long long x, int u = 1, int L = 1, int R = n){
		if(InRange(L, R, l, r)) maketag(u, R - L + 1, x);
		else if(!OutofRange(L, R, l, r)){
			int m = (L + R) / 2;
			pushdown(u, L, R);
			update(l, r, x, u * 2, L, m);
			update(l, r, x, u * 2 + 1, m + 1, R);
			pushup(u);
		}
	}
};

怎么使用呢？

定义：Segment a;

使用：构造 a.build()，区间修改 a.update(x,y,k)，区间查询 a.query(x,y)。其中，$x,y$ 为区间，$k$ 为修改值。注意有些函数的值顺序改了一下，记得调回来。此份代码是求区间和的代码。

?.菜单——动态开点线段树

const int maxn=100005;
int n;
struct dt_Segment_tree{
	struct node{
		int l,r,val,lzy;
		node(){
			l=r=val=lzy=0;
		}
	}tr[30*maxn];
	int tot=0;
	dt_Segment_tree(){
		tot++; // 建立根节点,可以直接在定义 tot 时写 'int tot=1;'
	}
	void pushup(int u)
	{
		tr[u].val=tr[tr[u].l].val+tr[tr[u].r].val;
	}
	void maketag(int u,int len,int x)
	{
		tr[u].lzy+=x;
		tr[u].val+=len*x;
	}
	void pushdown(int u,int l,int r)
	{
		if(!tr[u].l) tr[u].l=++tot;
		if(!tr[u].r) tr[u].r=++tot;
		int mid=(l+r)/2;
		maketag(tr[u].l,mid-l+1,tr[u].lzy);
		maketag(tr[u].r,r-mid,tr[u].lzy);
		tr[u].lzy=0;
	}
	bool InRangeOf(int L,int R,int l,int r)
	{
		return (l<=L)&&(R<=r);
	}
	bool OutRangeOf(int L,int R,int l,int r)
	{
		return (L>r)||(R<l);
	}
	void update(int l,int r,int x,int u=1,int L=1,int R=n)
	{
		if(InRangeOf(L,R,l,r)) maketag(u,R-L+1,x);
		else if(!OutRangeOf(L,R,l,r))
		{
			pushdown(u,L,R);
			int mid=(L+R)>>1;
			update(l,r,x,tr[u].l,L,mid);
			update(l,r,x,tr[u].r,mid+1,R);
			pushup(u);
		}
	}
	int query(int l,int r,int u=1,int L=1,int R=n)
	{
		if(InRangeOf(L,R,l,r)) return tr[u].val;
		else if(!OutRangeOf(L,R,l,r))
		{
			pushdown(u,L,R);
			int mid=(L+R)>>1;
			return query(l,r,tr[u].l,L,mid)+query(l,r,tr[u].r,mid+1,R);
		}
		else return 0;
	}
}

怎么使用呢？

定义：Segment a;

使用：区间修改 a.update(x,y,k)，区间查询 a.query(x,y)。其中，$x,y$ 为区间，$k$ 为修改值。注意有些函数的值顺序改了一下，记得调回来。此份代码是求区间和的代码。