零、说在前面
0.1 感谢
感谢百度百科、oi-wiki、洛谷的题目。
0.2 阅读前须知
作者很菜,不要看。如果有错误,私信即可,一周内回。
一、抽屉原理
1.1 第一抽屉原理
原理1: 把 n + k n+k n + k n n n 不少于 两件。n × 1 n×1 n × 1 n + k ( k ≥ 1 ) n+k(k≥1) n + k ( k ≥ 1 ) m n + 1 ( n ≠ 0 ) mn+1(n\ne 0) mn + 1 ( n = 0 ) n n n 不少于 ( m + 1 ) (m+1) ( m + 1 ) m m m n n n m n mn mn n n n
1.2 第二抽屉原理
把 ( m n - 1 ) (mn-1) ( mn - 1 ) n n n 至多 有 ( m − 1 ) (m-1) ( m − 1 )
例题:天选之人(?) 、取模
二、集合
2.1 定义
把一些单独的物体(数、坐标、函数、集合)合起来看成一个整体,就形成一个集合(或集)
2.2 集合的特点
确定性、互异性、无序性
2.3 集合的表示
大写字母,如集合 A , B , X A,B,X A , B , X
2.4 属于与不属于
若 a a a A A A a ∈ A a\in A a ∈ A a a a A A A a ∉ A a\not \in A a ∈ A
2.5 集合的表示
列举法{ 1 , 14 , 51 , 4 } , { ∅ , { 1 , 14 , 51 , 4 } , { ( 1 , 1 ) , ( 2 , 2 ) } , 1.14 } \{1,14,51,4\},\{\varnothing,\{1,14,51,4\},\{(1,1),(2,2)\},1.14\} { 1 , 14 , 51 , 4 } , { ∅ , { 1 , 14 , 51 , 4 } , {( 1 , 1 ) , ( 2 , 2 )} , 1.14 }
描述法114 114 114 { x ∣ x > 114 } \{x|x>114\} { x ∣ x > 114 }
图像法
区间法+ ∞ +\infty + ∞ − ∞ -\infty − ∞ ( a , b ) (a,b) ( a , b ) [ a , b ] [a,b] [ a , b ] [ a , b ) [a,b) [ a , b ) ( a , b ] (a,b] ( a , b ] ( 114 , 514 ) (114,514) ( 114 , 514 ) 114 , 514 114,514 114 , 514
符号法N N N { 0 , 1 , 2 , 3 , … } \{0,1,2,3,…\} { 0 , 1 , 2 , 3 , … } N ∗ N^* N ∗ N + N^+ N + { 1 , 2 , 3 , … } \{1,2,3,…\} { 1 , 2 , 3 , … } Z Z Z { … , − 1 , 0 , 1 , … } \{…,-1,0,1,…\} { … , − 1 , 0 , 1 , … } Q Q Q Q + Q+ Q + Q − Q- Q − R R R R + R+ R + R − R- R − C C C ∅ \varnothing ∅
2.6 集合基本关系
子集与真子集
子集S , T S,T S , T S S S T T T S S S T T T S ⊆ T S\subseteq T S ⊆ T S ⊆ S , ∅ ⊆ S S\subseteq S,\varnothing \subseteq S S ⊆ S , ∅ ⊆ S
真子集S ⊆ T S\subseteq T S ⊆ T T T T x x x x ∉ S x\not \in S x ∈ S S S S T T T
交集与并集A ⋂ B A\bigcap B A ⋂ B B ⋂ A B\bigcap A B ⋂ A A ⋂ B = { x ∣ x ∈ A , 且 x ∈ B } A\bigcap B=\{x|x∈A,\texttt且x∈B\} A ⋂ B = { x ∣ x ∈ A , 且 x ∈ B } A ⋃ B A\bigcup B A ⋃ B B ⋃ A B\bigcup A B ⋃ A A ⋃ B = { x ∣ x ∈ A , 或 x ∈ B } A\bigcup B=\{x|x∈A,\texttt或x∈B\} A ⋃ B = { x ∣ x ∈ A , 或 x ∈ B }
相等集合A ⊆ B A\subseteq B A ⊆ B B ⊆ A B\subseteq A B ⊆ A
补集
相对补集A A A B B B ∁ A B \complement_{A}B ∁ A B ∁ A B = { x ∣ x ∈ A , 且 x ∉ B } \complement_{A}B=\{x|x∈A,\texttt且x∉B\} ∁ A B = { x ∣ x ∈ A , 且 x ∈ / B }
绝对补集A A A U U U A A A ∁ U A \complement_{U}A ∁ U A
幂集A A A A A A A A A A A A 2 2 2 A A A A A A x x x 2 x 2^x 2 x
三、一一对应
前置知识:映射
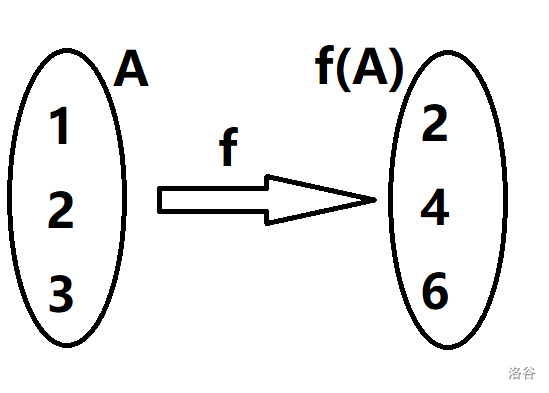
定义:两个非空集合 A A A B B B f f f A A A a a a B B B b b b A A A B B B f : A → B f:A→B f : A → B b b b a a a f f f b = f ( a ) b=f(a) b = f ( a ) a a a b b b f f f f f f f ( A ) f(A) f ( A )
一一对应:对于任意的 f : A → B f:A\to B f : A → B B B B A A A
四、错排公式
错排问题(伯努利-欧拉的装错信封的问题):有 n n n n n n i i i i i i
递推公式:T n = ( n − 1 ) ( T n − 1 + T n − 2 ) T_n=(n-1)(T_{n-1}+T_{n-2}) T n = ( n − 1 ) ( T n − 1 + T n − 2 )
推导:
将元素 n n n k ( k ≠ n ) k(k\ne n) k ( k = n ) n − 1 n-1 n − 1
若此时将元素 k k k n n n ( n − 1 ) T n − 2 (n-1)T_{n-2} ( n − 1 ) T n − 2 k k k n n n k k k n n n ( n − 1 ) T n − 1 (n-1)T_{n-1} ( n − 1 ) T n − 1
综上,T n = ( n − 1 ) ( T n − 1 + T n − 2 ) T_n=(n-1)(T_{n-1}+T_{n-2}) T n = ( n − 1 ) ( T n − 1 + T n − 2 )
错排问题的通项公式见5.5。
五、容斥原理
5.1 引入
七(7)班中,有 n n n m m m k ( k ≤ n 且 k ≤ m ) k(k\le n \texttt且 k\le m) k ( k ≤ n 且 k ≤ m ) n + m − k n+m-k n + m − k
5.2.1 经典容斥原理 - 1
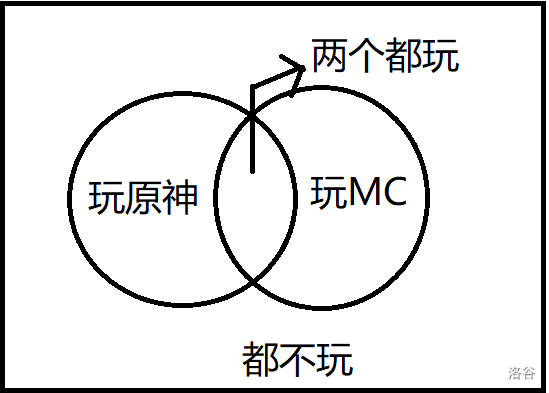
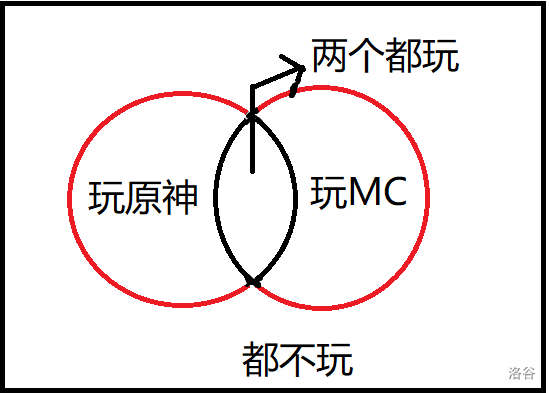
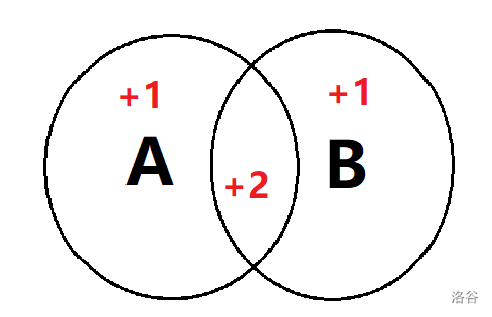
经典例题:有集合 A , B A,B A , B ∣ A ⋃ B ∣ = ∣ A ∣ + ∣ B ∣ − ∣ A ⋂ B ∣ |A\bigcup B|=|A|+|B|-|A\bigcap B| ∣ A ⋃ B ∣ = ∣ A ∣ + ∣ B ∣ − ∣ A ⋂ B ∣
答案加上 ∣ A ∣ + ∣ B ∣ |A|+|B| ∣ A ∣ + ∣ B ∣
显然多了 ∣ A ⋂ B ∣ |A\bigcap B| ∣ A ⋂ B ∣
5.2.2 经典容斥原理 - 2
经典例题:有集合 A , B , C A,B,C A , B , C ∣ A ⋃ B ⋃ C ∣ = ∣ A ∣ + ∣ B ∣ + ∣ C ∣ − ∣ A ⋂ B ∣ − ∣ A ⋂ C ∣ − ∣ B ⋂ C ∣ + ∣ A ⋂ B ⋂ C ∣ |A\bigcup B\bigcup C|=|A|+|B|+|C|-|A\bigcap B|-|A\bigcap C|-|B\bigcap C|+|A\bigcap B\bigcap C| ∣ A ⋃ B ⋃ C ∣ = ∣ A ∣ + ∣ B ∣ + ∣ C ∣ − ∣ A ⋂ B ∣ − ∣ A ⋂ C ∣ − ∣ B ⋂ C ∣ + ∣ A ⋂ B ⋂ C ∣
5.3 容斥原理通项
例题:有集合 A 1 ∼ A n A_1\sim A_n A 1 ∼ A n
∣ A 1 ⋃ A 2 ⋃ ⋯ ⋃ A n ∣ = ∑ 1 ≤ i ≤ n ∣ A i ∣ − ∑ 1 ≤ i ≤ j ≤ n ∣ A i ⋂ A j ∣ + ∑ 1 ≤ i ≤ j ≤ k ≤ n ∣ A i ⋂ A j ⋂ A k ∣ − ⋯ + ( − 1 ) n ∣ A 1 ⋂ A 2 ⋂ ⋯ ⋂ A n ∣ = ∑ k = 1 n ( − 1 ) k + 1 ∑ 1 ≤ i 1 ≤ i 2 ≤ ⋯ ≤ i k ∣ A i 1 ⋂ A i 2 ⋂ ⋯ ⋂ A i n ∣ \begin{aligned}
\left|A_1\bigcup A_2 \bigcup\cdots\bigcup A_n\right|&=\sum\limits_{1\le i\le n} \left|A_i\right|-\sum\limits_{1\le i\le j\le n} \left|A_i\bigcap A_j\right|+\sum\limits_{1\le i\le j\le k\le n} \left|A_i\bigcap A_j\bigcap A_k\right|-\cdots+(-1)^n \left|A_1\bigcap A_2\bigcap \cdots\bigcap A_n\right|\\
&=\sum\limits^{n}_{k=1}(-1)^{k+1}\sum\limits_{1\le i_1\le i_2\le \cdots\le i_k}\left|A_{i_1}\bigcap A_{i_2}\bigcap\cdots\bigcap A_{i_n}\right|
\end{aligned} A 1 ⋃ A 2 ⋃ ⋯ ⋃ A n = 1 ≤ i ≤ n ∑ ∣ A i ∣ − 1 ≤ i ≤ j ≤ n ∑ A i ⋂ A j + 1 ≤ i ≤ j ≤ k ≤ n ∑ A i ⋂ A j ⋂ A k − ⋯ + ( − 1 ) n A 1 ⋂ A 2 ⋂ ⋯ ⋂ A n = k = 1 ∑ n ( − 1 ) k + 1 1 ≤ i 1 ≤ i 2 ≤ ⋯ ≤ i k ∑ A i 1 ⋂ A i 2 ⋂ ⋯ ⋂ A i n 练习:出生点
5.4 二维前缀和
二维前缀和的本质是容斥原理
s i , j = s i , j − 1 + s i − 1 , j − s i − 1 , j − 1 + a i , j s_{i,j}=s_{i,j-1}+s_{i-1,j}-s_{i-1,j-1}+a_{i,j} s i , j = s i , j − 1 + s i − 1 , j − s i − 1 , j − 1 + a i , j ∑ i = x b x e ∑ j = y b y e a i , j = s x e , y e + s x b − 1 , y b − 1 − s x b − 1 , y e − s x e , y b − 1 \sum_{i = xb}^{xe} \sum_{j = yb}^{ye}a_{i,j}=s_{xe,ye}+s_{xb-1,yb-1}-s_{xb-1,ye}-s_{xe,yb-1} i = x b ∑ x e j = y b ∑ ye a i , j = s x e , ye + s x b − 1 , y b − 1 − s x b − 1 , ye − s x e , y b − 1 5.5 错排问题通项
正整数 1 , 2 , 3 , ⋯ , n 1,2,3,\cdots,n 1 , 2 , 3 , ⋯ , n n ! n! n ! k k k k k k ( n − 1 ) ! (n-1)! ( n − 1 )!
T n = n ! + n ! 1 ! − n ! 2 ! + ⋯ + ( − 1 ) n n ! n ! = ∑ i = 2 n ( − 1 ) i × n ! i ! T_n=n!+\dfrac{n!}{1!}-\dfrac{n!}{2!}+\cdots+(-1)^n\dfrac{n!}{n!}=\sum\limits^n_{i=2}\dfrac{(-1)^i\times n!}{i!} T n = n ! + 1 ! n ! − 2 ! n ! + ⋯ + ( − 1 ) n n ! n ! = i = 2 ∑ n i ! ( − 1 ) i × n ! 提出一个 n ! n! n ! T n = n ! ∑ i = 2 n ( − 1 ) i i ! T_n=n!\sum\limits^n_{i=2}\dfrac{(-1)^i}{i!} T n = n ! i = 2 ∑ n i ! ( − 1 ) i
六、康拓展开
七、排列数与组合数
7.1 排列数
定义n n n m ( m ≤ n ) m(m≤n) m ( m ≤ n ) n n n m m m n n n m ( m ≤ n ) m(m≤n) m ( m ≤ n ) n n n m m m A n m A^m_n A n m
计算
A n m = n × ( n − 1 ) × ( n − 2 ) × ⋯ × ( n − m + 1 ) = n ! ( n − m ) ! \begin{aligned}
A^m_n&=n\times (n-1)\times (n-2)\times \cdots\times (n-m+1)\\
&=\dfrac{n!}{(n-m)!}
\end{aligned} A n m = n × ( n − 1 ) × ( n − 2 ) × ⋯ × ( n − m + 1 ) = ( n − m )! n ! 7.2 组合数
定义n n n m ( m ≤ n ) m(m≤n) m ( m ≤ n ) n n n m m m n n n m ( m ≤ n ) m(m≤n) m ( m ≤ n ) n n n m m m C n m C^m_n C n m
计算
C n m = A n m A m m = n ! ( n − m ) ! × m ! \begin{aligned}
C^m_n&=\dfrac{A^m_n}{A_m^m}\\
&=\dfrac{n!}{(n-m)!\times m!}
\end{aligned} C n m = A m m A n m = ( n − m )! × m ! n !
注明C n m C_n^m C n m ( n m ) \begin{pmatrix}
n\\m
\end{pmatrix} ( n m )
7.3 组合数性质
C n m = C n n − m C^m_n=C^{n-m}_n C n m = C n n − m
递推公式C n − 1 k C^{k}_{n-1} C n − 1 k C n m C^m_n C n m
C n m = C n − 1 m + C n − 1 m − 1 C^m_n=C^m_{n-1}+C^{m-1}_{n-1} C n m = C n − 1 m + C n − 1 m − 1 C k n − 1 + C k − 1 n − 1 = C k n C^{n-1}_{k}+C^{n-1}_{k-1}=C^n_k C k n − 1 + C k − 1 n − 1 = C k n 7.4 计数方法
加法原理n n n 种 方法,每种方法有 a i a_i a i ∑ a i \sum a_i ∑ a i
乘法原理n n n 步 要做,每一步拥有 a i a_i a i ∏ a i \prod a_i ∏ a i
7.5 捆绑法、插空法
捆绑法用来处理相邻问题。在排列计数问题中,把需要相邻的元素“捆绑”在一起,视作一个元素参与排列。注意点:捆绑的元素最后还要“解绑”,把捆在一起的几个元素进行排列。
插空法用来处理不相邻问题。不能相邻的元素通常最后参与排列,通过插空的方式放在已排的元素之间。
7.6 隔板法
隔板法用来将相同的元素分组,并且每组至少有一个元素。
八、二项式定理
8.1 二项式定理
( x + y ) n = ∑ i = 0 n ( C n i × x i × y n − i ) (x+y)^n=\sum\limits_{i=\color{red}0}^n(C_n^i\times x^i\times y^{n-i}) ( x + y ) n = i = 0 ∑ n ( C n i × x i × y n − i ) 或表示为
( x + y ) n = [ x 0 ⋯ x n ] [ C n 0 ⋱ C n n ] [ 1 ⋯ 1 ] [ b 0 ⋮ b n ] (x+y)^n=[x^0\hspace{0.3cm}\cdots\hspace{0.3cm}x^n]\begin{bmatrix} C^0_n & & \\ & \ddots & \\& & C^n_n \end{bmatrix}\begin{bmatrix} & & 1\\ & \cdots & \\1 & & \end{bmatrix}\begin{bmatrix} b^0\\ \vdots \\b^n \end{bmatrix} ( x + y ) n = [ x 0 ⋯ x n ] C n 0 ⋱ C n n 1 ⋯ 1 b 0 ⋮ b n 8.2 二项式定理的简单推导
( x + y ) 1 = x + y (x+y)^1=x+y ( x + y ) 1 = x + y ( x + y ) 2 = x 2 + 2 x y + y 2 (x+y)^2=x^2+2xy+y^2 ( x + y ) 2 = x 2 + 2 x y + y 2 ( x + y ) 3 = x 3 + 3 x 2 y + 3 x y 2 + y 2 (x+y)^3=x^3+3x^2y+3xy^2+y^2 ( x + y ) 3 = x 3 + 3 x 2 y + 3 x y 2 + y 2 ⋯ \cdots ⋯ ( x + y ) n = ∑ i = 0 n ( C n i x i y n − i ) (x+y)^n=\sum\limits_{i=0}^n(C_n^ix^iy^{n-i}) ( x + y ) n = i = 0 ∑ n ( C n i x i y n − i ) 8.3 二项式定理的严谨推导
组合证法a 1 ∼ a n a_1\sim a_n a 1 ∼ a n
( x + y ) n = ( x + y ) × ( x + y ) × ( x + y ) × ( x + y ) × ⋯ × ( x + y ) ⏟ n 个 ( x + y ) = a 1 x n + a 2 x n − 1 y + a 3 x n − 2 y 2 + ⋯ + a n y n \begin{aligned}(x+y)^n&=\underbrace{(x+y)\times (x+y)\times (x+y)\times (x+y)\times\cdots \times (x+y)}_{n\texttt{个}(x+y)}\\
&=a_1x^n+a_2x^{n-1}y+a_3x^{n-2}y^2+\cdots+a_ny^n
\end{aligned} ( x + y ) n = n 个 ( x + y ) ( x + y ) × ( x + y ) × ( x + y ) × ( x + y ) × ⋯ × ( x + y ) = a 1 x n + a 2 x n − 1 y + a 3 x n − 2 y 2 + ⋯ + a n y n 对于 i i i a i a_i a i n n n ( x + y ) (x+y) ( x + y ) 组合 \color{red}\texttt{组合} 组合 i i i x x x a i = C n i a_i=C_n^i a i = C n i
数学归纳法m = 1 m=1 m = 1 m = n m=n m = n m = n + 1 m=n+1 m = n + 1
( x + y ) n + 1 = x ( x + y ) n + y ( x + y ) n = x ∑ i = 0 n ( C n i x i y n − i ) + y ∑ i = 0 n ( C n i x i y n − i ) = ∑ i = 0 n ( C n i x i + 1 y n − i ) + ∑ i = 0 n ( C n i x i y n − i + 1 ) = ∑ i = 0 n ( C n i x i + 1 y n − i ) + ∑ i = 1 n ( C n i x i y n − i + 1 ) + y n + 1 = ∑ i = 1 n + 1 ( C n i − 1 x i y n − i + 1 ) + ∑ i = 1 n ( C n i x i y n − i + 1 ) + y n + 1 = x n + 1 + y n + 1 + ∑ i = 1 n ( C n i − 1 x i y n − i + 1 ) + ∑ i = 1 n ( C n i x i y n − i + 1 ) = x n + 1 + y n + 1 + ∑ i = 1 n ( C n i − 1 + C n i ) ( x i y n − i + 1 ) = x n + 1 + y n + 1 + ∑ i = 1 n ( C n + 1 i x i y x − i + 1 ) (帕斯卡法则) = ∑ i = 0 m ( C m i x i y m − i ) \begin{aligned}(x+y)^{n+1}&=x(x+y)^n+y(x+y)^n\\
&=x\sum\limits_{i=0}^n(C_n^ix^iy^{n-i})+y\sum\limits_{i=0}^n(C_n^ix^iy^{n-i})\\
&=\sum\limits_{i=0}^n(C_n^ix^{i+1}y^{n-i})+\sum\limits_{i=0}^n(C_n^ix^iy^{n-i+1})\\
&=\sum\limits_{i=0}^n(C_n^ix^{i+1}y^{n-i})+\sum\limits_{i=1}^n(C_n^ix^iy^{n-i+1})+y^{n+1}\\
&=\sum\limits_{i=1}^{n+1}(C_{n}^{i-1}x^{i}y^{n-i+1})+\sum\limits_{i=1}^n(C_n^ix^iy^{n-i+1})+y^{n+1}\\
&=x^{n+1}+y^{n+1}+\sum\limits_{i=1}^{n}(C_{n}^{i-1}x^{i}y^{n-i+1})+\sum\limits_{i=1}^n(C_n^ix^iy^{n-i+1})\\
&=x^{n+1}+y^{n+1}+\sum\limits^n_{i=1}(C^{i-1}_n+C^{i}_n)(x^iy^{n-i+1})\\
&=x^{n+1}+y^{n+1}+\sum\limits^n_{i=1}(C^i_{n+1}x^iy^{x-i+1}){\texttt{\color{red}(帕斯卡法则)}}\\
&=\sum\limits_{i=0}^m(C_m^ix^iy^{m-i})
\end{aligned} ( x + y ) n + 1 = x ( x + y ) n + y ( x + y ) n = x i = 0 ∑ n ( C n i x i y n − i ) + y i = 0 ∑ n ( C n i x i y n − i ) = i = 0 ∑ n ( C n i x i + 1 y n − i ) + i = 0 ∑ n ( C n i x i y n − i + 1 ) = i = 0 ∑ n ( C n i x i + 1 y n − i ) + i = 1 ∑ n ( C n i x i y n − i + 1 ) + y n + 1 = i = 1 ∑ n + 1 ( C n i − 1 x i y n − i + 1 ) + i = 1 ∑ n ( C n i x i y n − i + 1 ) + y n + 1 = x n + 1 + y n + 1 + i = 1 ∑ n ( C n i − 1 x i y n − i + 1 ) + i = 1 ∑ n ( C n i x i y n − i + 1 ) = x n + 1 + y n + 1 + i = 1 ∑ n ( C n i − 1 + C n i ) ( x i y n − i + 1 ) = x n + 1 + y n + 1 + i = 1 ∑ n ( C n + 1 i x i y x − i + 1 ) ( 帕斯卡法则 ) = i = 0 ∑ m ( C m i x i y m − i ) 所以对于 n ∈ N + n\in N^+ n ∈ N + ( x + y ) n = ∑ i = 0 n ( C n i x i y n − i ) (x+y)^n=\sum\limits_{i=0}^n(C_n^ix^iy^{n-i}) ( x + y ) n = i = 0 ∑ n ( C n i x i y n − i )
8.4 杨辉三角
杨辉三角:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
......对于第 i i i j j j y ( i , j ) = y ( i − 1 , j − 1 ) + y ( i − 1 , j ) , y ( i , 1 ) = y ( i , i ) = 1 y(i,j)=y(i-1,j-1)+y(i-1,j),y(i,1)=y(i,i)=1 y ( i , j ) = y ( i − 1 , j − 1 ) + y ( i − 1 , j ) , y ( i , 1 ) = y ( i , i ) = 1 y ( i , j ) y(i,j) y ( i , j ) C i j C_i^j C i j
8.5 一些常用的式子
∑ C n i = 2 n \sum C_n^i=2^n ∑ C n i = 2 n ∑ C n i a i = ( a + 1 ) n \sum C_n^ia^i=(a+1)^n ∑ C n i a i = ( a + 1 ) n ∑ ( C n i ) 2 = C 2 n n \sum (C_n^i)^2=C_{2n}^n ∑ ( C n i ) 2 = C 2 n n
例题:Necklace
九、卡特兰数
9.1 卡特兰数的定义
卡特兰数的定义n n n 2 2 2 m m m 0 0 0 1 1 1
1 , 1 , 2 , 5 , 14 , 42 , 132 , 429 , 1430 , 4862 , 16796 , 58786 , 208012 , 742900 , 2674440 , 9694845 , 35357670 , 129644790 , 477638700 , 1767263190 , 6564120420 , 24466267020 , 91482563640 , 343059613650 , 1289904147324 , 4861946401452 , . . . 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ... 1 , 1 , 2 , 5 , 14 , 42 , 132 , 429 , 1430 , 4862 , 16796 , 58786 , 208012 , 742900 , 2674440 , 9694845 , 35357670 , 129644790 , 477638700 , 1767263190 , 6564120420 , 24466267020 , 91482563640 , 343059613650 , 1289904147324 , 4861946401452 , ...
递推公式h ( i ) h(i) h ( i ) i i i
h ( n + 1 ) = h ( n ) h ( 0 ) + h ( n − 1 ) h ( 1 ) + ⋯ + h ( 0 ) ( n ) h(n+1)=h(n)h(0)+h(n-1)h(1)+\cdots+h(0)(n) h ( n + 1 ) = h ( n ) h ( 0 ) + h ( n − 1 ) h ( 1 ) + ⋯ + h ( 0 ) ( n ) 即
h ( n ) = ∑ i = 0 n − 1 h ( i ) h ( n − i ) h(n)=\sum\limits^{n-1}_{i=0}h(i)h(n-i) h ( n ) = i = 0 ∑ n − 1 h ( i ) h ( n − i ) 还可以写作:
h ( n ) = h ( n − 1 ) ( 4 n − 2 ) n + 1 h(n)=\dfrac{h(n-1)(4n-2)}{n+1} h ( n ) = n + 1 h ( n − 1 ) ( 4 n − 2 ) h ( n ) = C 2 n n n + 1 ( n ∈ N ) h(n)=\dfrac{C_{2n}^n}{n+1}\hspace{0.5cm}(n\in N) h ( n ) = n + 1 C 2 n n ( n ∈ N ) h ( n ) = C 2 n n − C 2 n n − 1 h(n)=C^n_{2n}-C^{n-1}_{2n} h ( n ) = C 2 n n − C 2 n n − 1 9.2 c++求卡特兰数
void catalan ()
int i, j, len, carry, temp;
a[1 ][0 ] = b[1 ] = 1 ;
len = 1 ;
for (i = 2 ; i <= 100 ; i++)
{
for (j = 0 ; j < len; j++)
a[i][j] = a[i-1 ][j]*(4 *(i-1 )+2 );
carry = 0 ;
for (j = 0 ; j < len; j++)
{
temp = a[i][j] + carry;
a[i][j] = temp % 10 ;
carry = temp / 10 ;
}
while (carry)
{
a[i][len++] = carry % 10 ;
carry /= 10 ;
}
carry = 0 ;
for (j = len-1 ; j >= 0 ; j--)
{
temp = carry*10 + a[i][j];
a[i][j] = temp/(i+1 );
carry = temp%(i+1 );
}
while (!a[i][len-1 ])
len --;
b[i] = len;
}
}by 百度百科
9.3 卡特兰数的应用
十、欧拉筛
10.1 质数
只能被 1 1 1
当 N N N 1 1 1 N N N N log N \dfrac{N}{\log N} log N N
在某个正整数 N N N log N \log N log N
如何判断一个整数 n n n 2 2 2 n \sqrt{n} n O ( n ) O(\sqrt{n}) O ( n )
a a a n a \dfrac{n}{a} a n 1 1 1 n \sqrt{n} n 2 2 2 n \sqrt{n} n
10.2 筛法(埃式筛)
从小到大,依次将每个质数的倍数删去(若遍历到一个数时,其没有被删去,则可知这个数是质数),最终留下的全是质数。
f[1 ]=false ;
for (int i=2 ;i<=n;i++) f[i]=true ;
for (int i=2 ;i<=n;i++)
{
if (f[i]==true )
for (long long j=(long long )i*i;j<=n;j+=i)
f[j]=false ;
}
j j j i × i i\times i i × i 2 × i 2\times i 2 × i 3 × i 3\times i 3 × i i = 2 , i = 3 i=2,i=3 i = 2 , i = 3 时间复杂度 O ( n log log n ) O(n\log\log n) O ( n log log n )
10.3 筛法(欧拉筛)
数字 30 30 30 3 × 10 、 2 × 15 、 5 × 6 3\times 10、2\times15、5\times 6 3 × 10 、 2 × 15 、 5 × 6 2 2 2 4 、 6 、 8 、 10 、 12 ⋯ 4、6、8、10、12\cdots 4 、 6 、 8 、 10 、 12 ⋯ 3 3 3 9 、 15 、 21 ⋯ 9、15、21\cdots 9 、 15 、 21 ⋯ 5 5 5 25 、 35 、 55 ⋯ 25、35、55\cdots 25 、 35 、 55 ⋯
我们记求解到 i i i p p p i i i i × p 1 、 i × p 2 i\times p_1、i\times p_2 i × p 1 、 i × p 2 a = a= a = b × b\times b × c c c c c c p j = b p_j=b p j = b a a a
每个合数还是没有只被它的最小质因数筛。
如 60 60 60 3 × 20 3\times 20 3 × 20 15 × 4 15\times 4 15 × 4
f[1 ]=false ;
for (int i=2 ;i<=n;i++) f[i]=true ;
for (int i=2 ;i<=n;i++)
{
if (f[i]==true ) p[cnt++]=i;
for (int j=1 ;j<=cnt&&i*p[j]<=n;j++)
f[p[j]*i]=false ;
}
内层循环加上一句if(i%p[j]==0)break;即可。为什么?
此时,比 p[j] 小的质数 p[k] 不满足 p[k] ∣ i |i ∣ i i i i p[j] 大,因为如果有小的那 j j j i × i\times i × p[k] 的最小质因数肯定是 p[k]。
同理可证,设有比 p[j] 大的质数 p[l] ,则删 p[l] × i \times i × i p[l] × i / \times i / × i / p[j] 是 x x x i i i x x x x × x\times x × p[j] 又会把这个数字筛一次。
时间复杂度 O ( n ) O(n) O ( n )
f[1 ]=false ;
for (int i=2 ;i<=n;i++) f[i]=true ;
for (int i=2 ;i<=n;i++)
{
if (f[i]==true ) p[cnt++]=i;
for (int j=1 ;j<=cnt&&i*p[j]<=n;j++)
{
f[p[j]*i]=false ;
if (i%p[j]==0 )break ;
}
}十一、逆元
11.1 逆元
若 a , x , p a,x,p a , x , p
a x ≡ 1 ( m o d p ) ax\equiv 1 \pmod p a x ≡ 1 ( mod p ) 则称 x x x p p p a a a x = a − 1 x=a^{-1} x = a − 1
12.1 求逆元
exGCD法
快速幂法
线性求 1 ∼ n 1\sim n 1 ∼ n oi.wiki
inv[1 ] = 1 ;
for (int i = 2 ; i <= n; ++i) {
inv[i] = (long long )(p - p / i) * inv[p % i] % p;
}by oi-wiki
线性求 a 1 ∼ a n a_1\sim a_n a 1 ∼ a n
十二、exGCD(扩展欧几里得)
12.0 不定方程
已知有多个个未知数,1 1 1
不定方程组同理。
12.1 扩展欧几里得是什么?
关于 x , y x,y x , y
a x + b y = gcd ( a , b ) ax+by=\gcd(a,b) a x + b y = g cd( a , b ) 12.2 求解方程
void exgcd (int a, int b, int &x, int &y)
if (b == 0 )
{
x = 1 , y = 0 ;
return ;
}
exgcd (b, a % b, y, x);
y -= a / b * x;
}12.3 exGCD 求逆元
可以从 a x ≡ x ( m o d p ) ax \equiv x\pmod{p} a x ≡ x ( mod p ) ∃ y , a x + p y = 1 \exists y,ax+py=1 ∃ y , a x + p y = 1 ∃ \exists ∃ a , p a,p a , p a a a p p p gcd ( a , p ) = 1 \gcd(a,p)=1 g cd( a , p ) = 1 a a a p p p a ⊥ p a\perp p a ⊥ p
void exgcd (int a, int b, int &x, int &y)
if (b == 0 )
{
x = 1 , y = 0 ;
return ;
}
exgcd (b, a % b, y, x);
y -= a / b * x;
}
int inv (int a, int p)
int x, y;
exgcd (a, p, x, y);
return x;
}12.4 exGCD求 a 1 ∼ a n a_1\sim a_n a 1 ∼ a n
记 p i = ∏ j = 1 i a j p_i=\prod\limits
_{j=1}^{i} a_j p i = j = 1 ∏ i a j
那么我们可以用exGCD求出 p i − 1 {p_i}^{-1} p i − 1 v i v_i v i
此时 v i × a n = ( ∏ i = 1 n − 1 a i ) − 1 v_i\times a_n={
\begin{pmatrix}
\prod\limits_{i=1}^{n-1}a_i
\end{pmatrix}}
^{-1} v i × a n = ( i = 1 ∏ n − 1 a i ) − 1 v i − 1 v_{i-1} v i − 1 v 1 ∼ v n v_1\sim v_n v 1 ∼ v n
则 a i − 1 = v i × p i − 1 {a_i}^{-1}=v_i\times p_{i-1} a i − 1 = v i × p i − 1
12.5 exGCD求 a b m o d p \dfrac{a}{b}\bmod p b a mod p
设 a b ≡ x ( m o d p ) \dfrac{a}{b}\equiv x\pmod p b a ≡ x ( mod p )
那么 a ≡ b x ( m o d p ) a\equiv bx\pmod p a ≡ b x ( mod p )
记 x ′ = x a x'=\dfrac{x}{a} x ′ = a x b x ′ ≡ 1 ( m o d p ) bx'\equiv 1\pmod p b x ′ ≡ 1 ( mod p )
这个方程是可以解的。最终 x = a x ′ x=ax' x = a x ′
十三、中国剩余定理
13.0 中国剩余定理的来源
「物不知数」问题:有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
该问题最早见于《孙子算经》中,并有该问题的具体解法。宋朝数学家秦九韶于 1247 年《数书九章》卷一、二《大衍类》对「物不知数」问题做出了完整系统的解答。上面具体问题的解答口诀由明朝数学家程大位在《算法统宗》中给出:
三人同行七十希,五树梅花廿一支,七子团圆正半月,除百零五便得知。
13.1 线性同余方程组
给定 n n n
{ x ≡ a 1 ( m o d m 1 ) x ≡ a 2 ( m o d m 2 ) ⋯ x ≡ a n ( m o d m n ) \begin{cases}x\equiv a_1\pmod {m_1}\\x\equiv a_2\pmod {m_2}\\\cdots\\x\equiv a_n\pmod {m_n}\end{cases} ⎩ ⎨ ⎧ x ≡ a 1 ( mod m 1 ) x ≡ a 2 ( mod m 2 ) ⋯ x ≡ a n ( mod m n ) m i m_i m i 两两互质 ,求 x x x
13.2 中国剩余定理(CRT)
记 M = ∏ m i M=\prod m_i M = ∏ m i M i = M m i M_i=\dfrac{M}{m_i} M i = m i M t i t_i t i M i M_i M i m i m_i m i
则:
x = k M + ∑ i = 1 n a i t i M i x=kM+\sum_{i=1}^{n} a_it_iM_i x = k M + i = 1 ∑ n a i t i M i 13.3 扩展中国剩余定理(exCRT)
如果 m i m_i m i
那什么是 exCRT 呢?
如果我们知道两个同余方程,将其合并成一个,这样就可以一个接着一个合并了。
见?
十四、裴蜀定理
方程 a x + b y = c ax+by=c a x + b y = c 当且仅当 gcd ( a , b ) ∣ c \gcd(a,b)|c g cd( a , b ) ∣ c
十五、数论分块
十六、同余与剩余系
十七、费马小定理
lhq:费马小
费马小定理:如果质数 p p p a ⊥ p a\bot p a ⊥ p a p − 1 ≡ 1 ( m o d p ) a^{p-1}\equiv 1\pmod p a p − 1 ≡ 1 ( mod p )
另一个形式:对于任意整数 a a a a p ≡ a ( m o d p ) a^p\equiv a\pmod p a p ≡ a ( mod p )
总所周知,费马小也是可以求逆元的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号