线段树(进阶)
2. 主席树
2.1 【模板】可持久化线段树 1(可持久化数组)
维护一个可持久化数组。
- 从某一个历史版本修改某个数的值
- 求某个版本的某处值。
每次都会进行版本更新(第二个操作生成一个完全一样的版本)
2.2 主席树
主席树的全称:可持久化线段树。
版本相当于一个树:
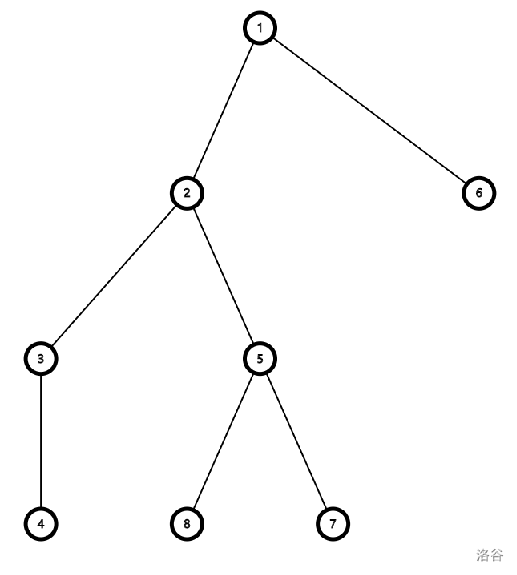
如果没有版本问题,完全可以直接用数组,但这里我们还是使用线段树:
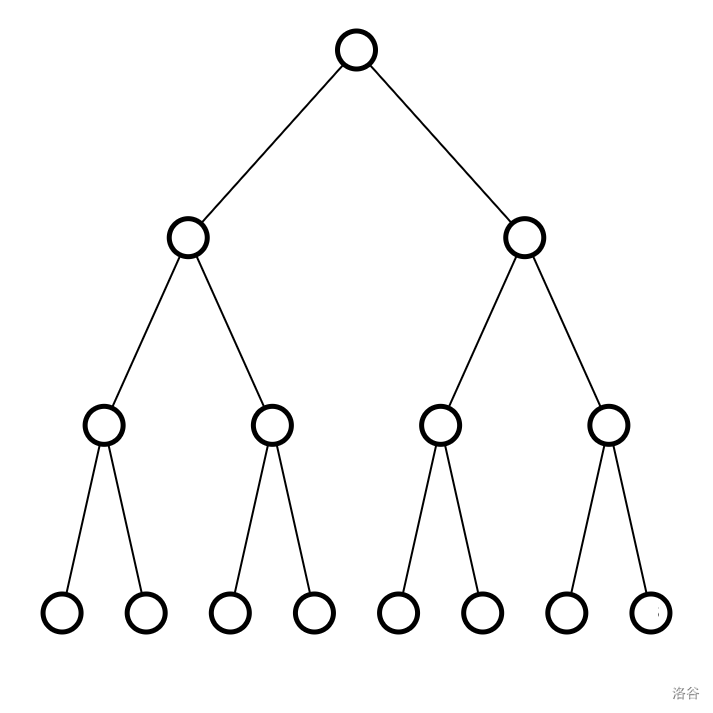
接下来我们为 ,。
很显然,未改变的节点约为 个,而且 为链。如果直接再建一棵线段树,在空间上是很亏的。所以考虑直接这么建:
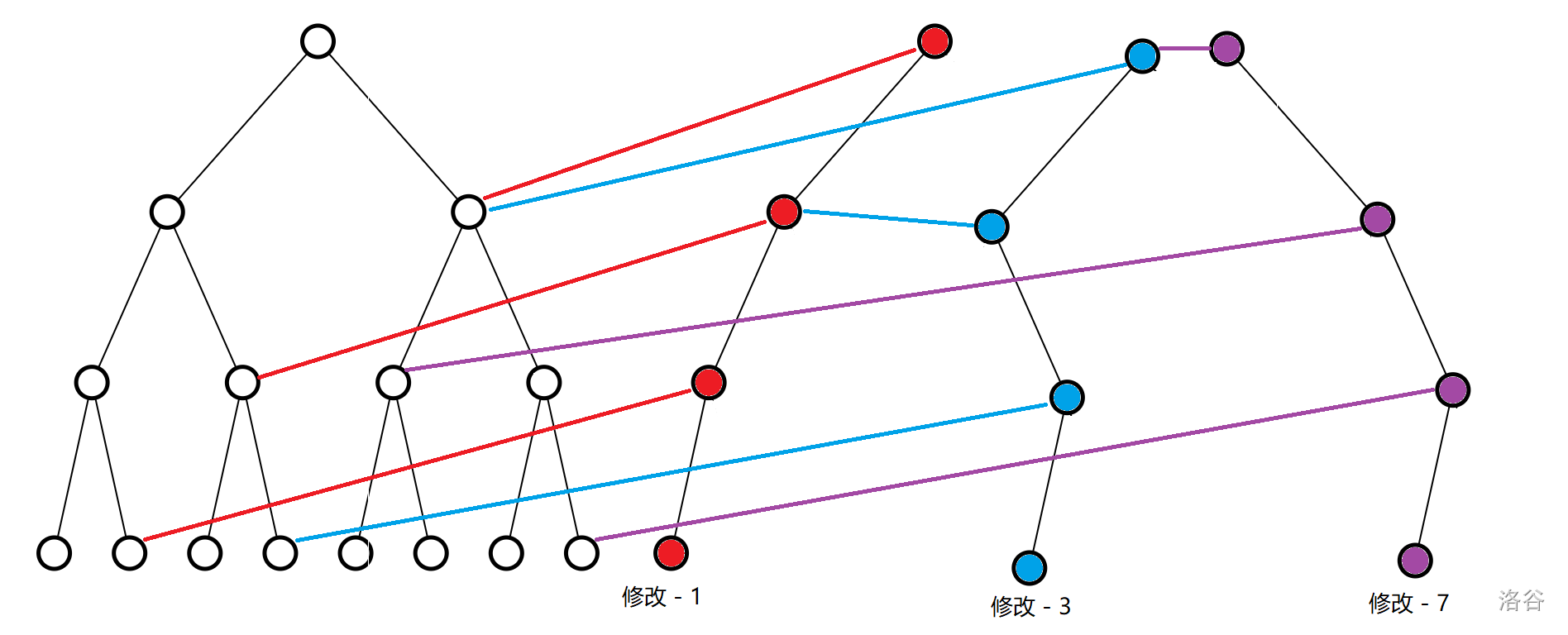
尽管图很抽象,但的确很抽象。
解释一下:由于每一次分叉会差一个节点,那么新建的线段树应该让所有节点(除了叶子)连上其他未接上的点。
很显然,每一次增加 个点,总用点不超过 ,不好爆。
观察主席树,很显然每个节点不止一个直接祖先,祖先也不止一个。
通过主席树,如果想查询,直接找版本就可以了。
可问题是:怎么存储和加边呢?
线段树使用左儿子 ,右儿子 的办法来存储的。
而主席树用的是结构体:
struct tree{
int l,r,val;
//左儿子,右儿子,权值
}那么加边就很简单了,指一下就可以了。
如何查询呢?我们可以用 个数组来存历史版本。
然后,就没有然后了。
封装主席树:
struct ZX__tree{
struct tree{
int l,r,val;
};
tree a[32000006];
int tr[32000006];
int top;
int build(int node,int l=1,int r=n)
{
node=++top;
if(l==r)
{
a[node].val=read();
return node;
}
int mid=(l+r)/2;
a[node].l=build(a[node].l,l,mid);
a[node].r=build(a[node].r,mid+1,r);
return node;
}
int add(int &node)
{
top++;
a[top]=a[node];
return top;
}
int update(int w,int val,int node,int l=1,int r=n)
{
node=add(node);
if(l==r) a[node].val=val;
else
{
int mid=(l+r)/2;
if(w<=mid) a[node].l=update(w,val,a[node].l,l,mid);
else a[node].r=update(w,val,a[node].r,mid+1,r);
}
return node;
}
int query(int w,int node,int l=1,int r=n)
{
if(l==r) return a[node].val;
else
{
int mid=(l+r)/2;
if(w<=mid) return query(w,a[node].l,l,mid);
else return query(w,a[node].r,mid+1,r);
}
}
}a;3. 扫描线
3.1 逆序对
水。
3.2 面积并
给定 个矩形,求矩形并
我们可以用一个线从左往右(别问为什么图是从下往上)扫,统计对于每次扫到的区间面积。
我们可以对每个矩形左边和右边用 和 标记, 表示需要计算, 表示不许计算。那么就能轻松维护他们的面积。
图和代码见 oi.wiki
3.3 统计矩形周长
我们可以从左往右,统计出红色线。同理,可以求出其他颜色的线
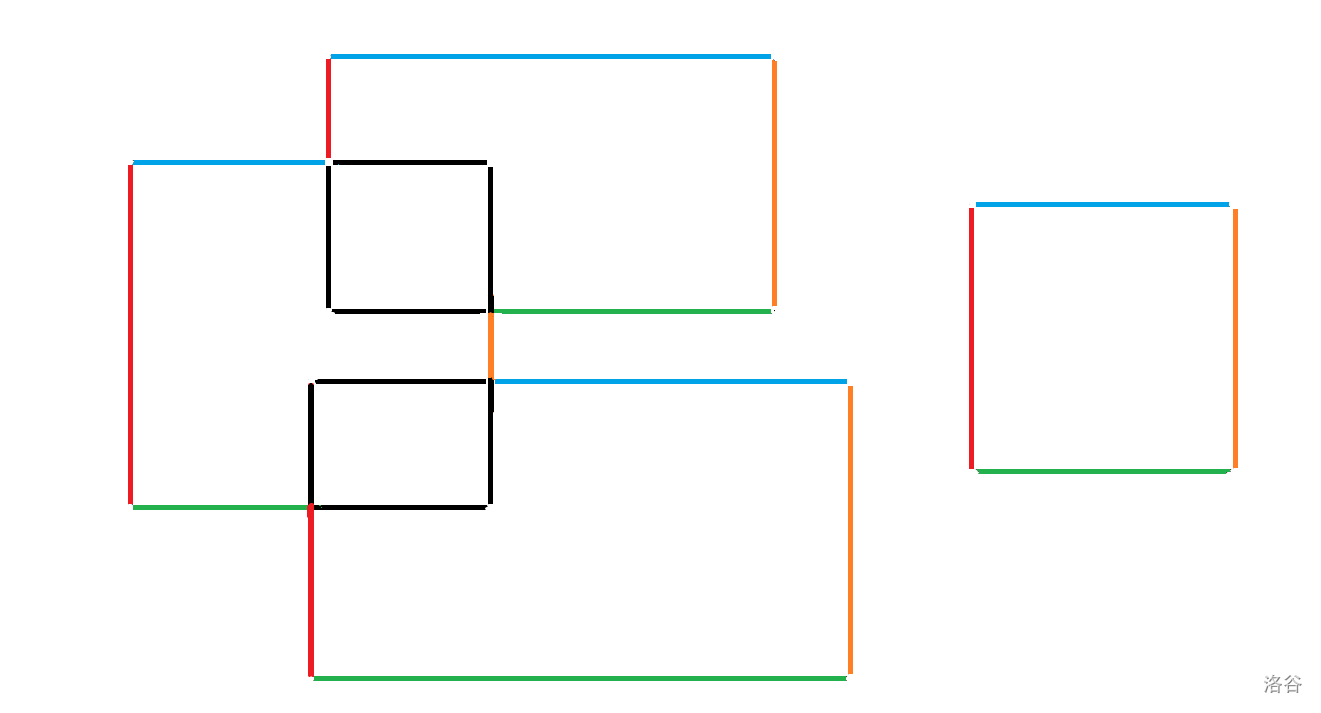
3.4 窗口的星星
3.5 总结
- 相较于主席树而言,通过扫一维,能够用线段树等数据结构更加方便的维护另一维的信息
- 但是通常要求离线



 浙公网安备 33010602011771号
浙公网安备 33010602011771号