树链剖分（树剖）

0. ？

0.1 ？

本文章仅介绍剖分，如果是精神病，请去找@Grow2011 。

0.2 ？

0.3 ？

$dep_x=depth_x$：$x$ 节点的深度

$fa_x$：$x$ 节点的父亲

$top_x$：$x$ 重链链顶。

本文章的目的：让大家粗略学会熟练剖粪

1. 树链剖分

1.1 什么是树链剖分

将一棵树剖分成一些链，这就叫树链剖分。

例如：

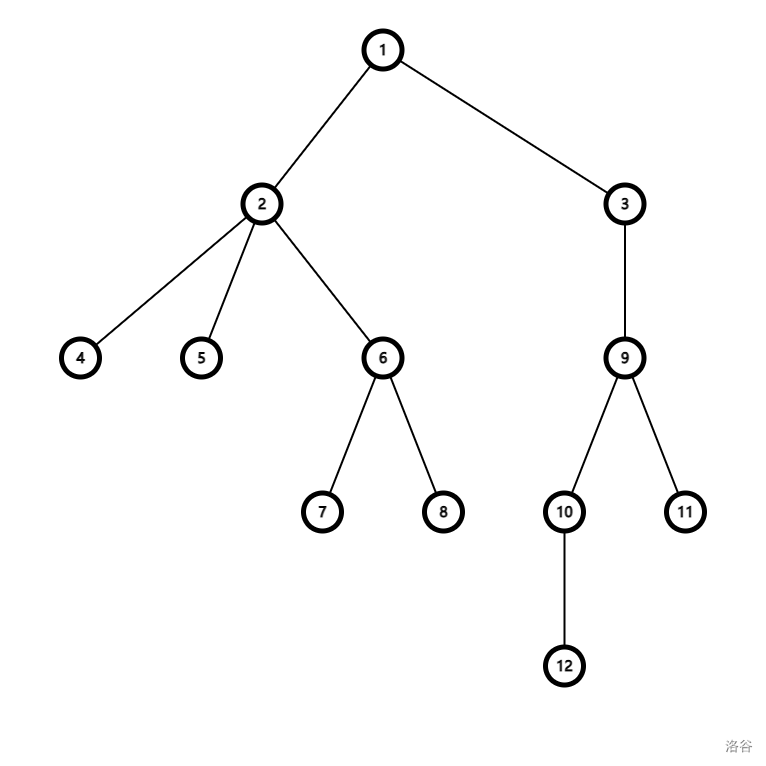
可以剖分成：

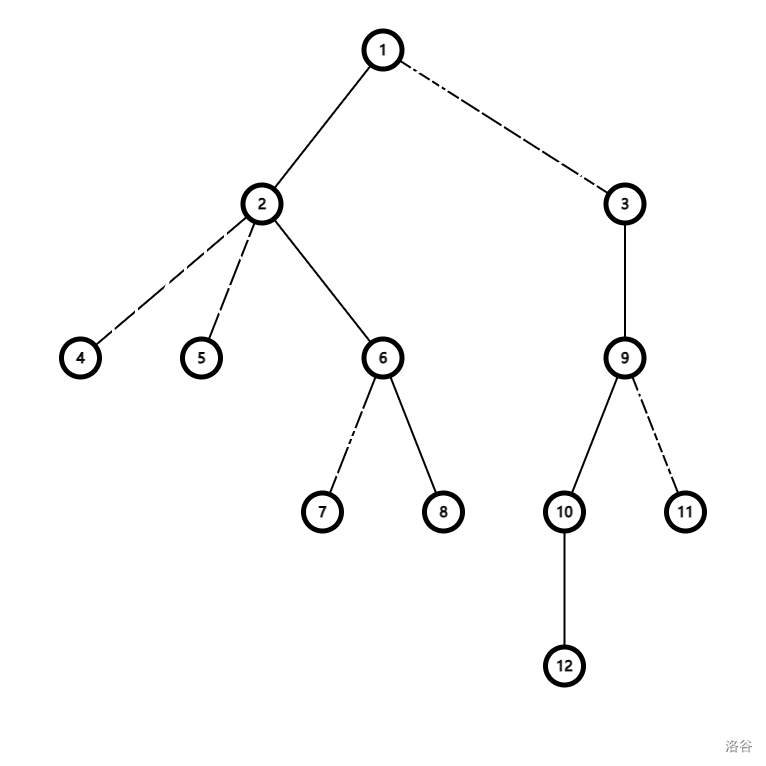
1.2 重链剖分

就像这棵树：

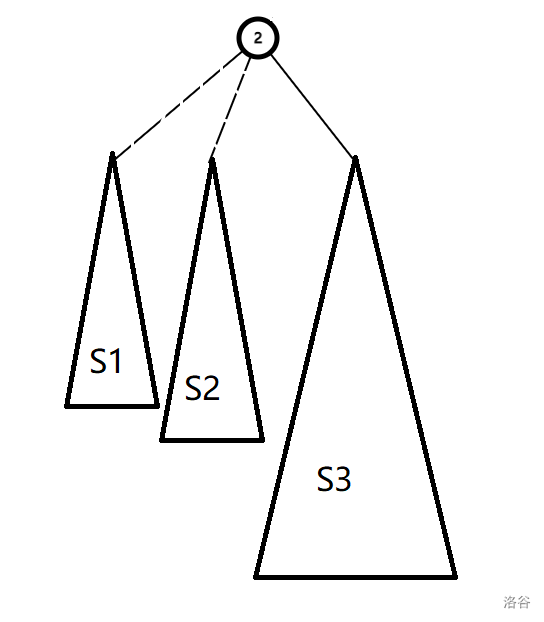
那么我们直接向子树大小最大的子树连接就可以了。

到这个子树的连边就是重边，其他连边就是轻边。所有的重边统称重链。

1.3 重链剖分的性质

1. 树上的每个节点都属于一条重链；
2. 重链将整棵树 完全剖分；
3. 一棵树最多被分为 $\log n$ 条链；（重点）
4. 同一子树内的 DFS 序是连续的。

对性质 $3$ 进行证明。

每一次经过一次轻边，大小至少减小一半。$n$ 个节点，每次减一半，就只有 $\log n$ 条链。

1.4 树到序列

前置：DFS序。

如果我们要为 $x$ 节点全体增加 $v$，就可以为 $\text{dfn}_{l_x}\gets \text{dfn}_{l_x}-x,\text{dfn}_{r_x}\gets \text{dfn}_{r_x}+x,$

然而问题一般是这样的：为链 $x\to y$ 增加 $v$。

这个时候我们就需要寻找这些区间：

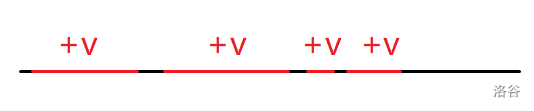
根据性质 1，所有节点所在的重链一定都在这条链上，那么可以想到他是这样的区间：

$x\to top_x,fa_{top_x}\to top_{fa_{top_x}},\cdots$。

暴力加即可。

根据性质 3，时间复杂度不超过 $O(n\log n)$。

1.5 重链剖分LCA

考虑我们是如何用倍增求解 LCA 的。首先我们 将两个节点提到同一高度，然后将两个节点一起向上跳。对于树链剖分也可以使用这样的思想。

在向上跳的过程中，如果当前节点在重链上，向上跳到重链顶端，如果当前节点不在重链上，向上跳一个节点。如此直到两节点相同。