连通性问题

1. 联通分量

分量说明我们探讨的是子图。

OI 中重要的联通分量是这几个：

1. 点双 无向图
2. 边双 无向图
3. 强连通 有向图

2. 点双联通

2.1 点双联通

在一张连通的无向图中，对于两个点 $u$ 和 $v$，如果无论删去哪个点（只能删去一个，且不能删 $u$ 和 $v$ 自己）都不能使它们不连通，我们就说 $u$ 和 $v$ 点双连通。

如果两点之间有两条完全不相交的路径，那么他们点双。

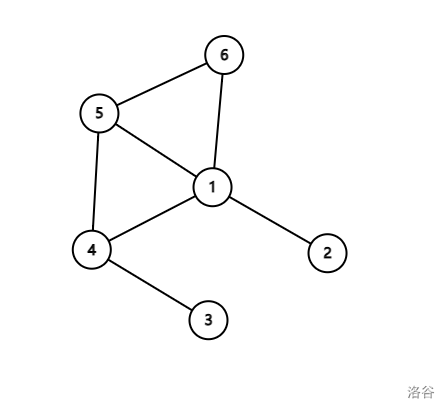
如图，$(2,4)$ 就不是点双，这就不是一个点双联通分量。

2.2 割点

如果能删去一个点 $x$，使得子图不为一个点双联通分量，那么 $x$ 就被称为割点。

注意：一个点可能在多个点双之内。

3. 边双联通

3.1 边双联通

在一张连通的无向图中，对于两个点 $u$ 和 $v$，如果无论删去哪条边（只能删去一条）都不能使它们不连通，我们就说 $u$ 和 $v$ 边双连通。

如果两点之间有两条边不相交的的路径，那么他们边双。

如图，$(2,4)$ 就不是边双，这就不是一个边双联通分量。

3.2 割边（桥）

如果能删去一条边 $x$，使得子图不为一个边双联通分量，那么 $x$ 就被称为割边。

注意：一个点只可能在一个边双之内。

3.3 环

环是构成点双和边双的基础。

一条链不存在边双。一条大于 $2$ 的节点的链不存在点双。

4. 强连通分量

4.1 强连通分量

在一张有向图中，对于两个点 $u$ 和 $v$，如果他们能互相到达，那么我们就说 $u$ 和 $v$ 强连通。

强连通分量的定义是：有向图 $G$ 中任意两个结点连通。

4.2 强连通分量的性质

环是构成强连通分量的基础。

任意两条个极大的强连通分量没有交点（不然他们可以合并成一个强联通分量）

如果将所有极大的强连通分量缩点，那么缩出来的是一张 $\color{red}\operatorname{DAG}$（有向无环图）。

5. 搜索树

以这张图为例：

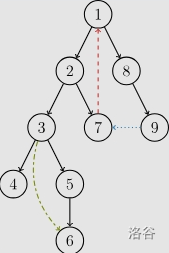
显然，这是一颗生成树，主要有四种边：

1. 树边（tree edge）：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
2. 反祖边（back edge）：示意图中以红色边表示（即 $7 \to 1$），也被叫做回边，即指向祖先结点的边。
3. 横叉边（cross edge）：示意图中以蓝色边表示（即 $9 \to 7$），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前结点的祖先。
4. 前向边（forward edge）：示意图中以绿色边表示（即 $3 \to 6$），它是在搜索的时候遇到子树中的结点的时候形成的。

定义：

1. $\textit{dfn}_u$：深度优先搜索遍历时结点 u 被搜索的次序。
2. $\textit{low}_u$：在 u 的子树中能够回溯到的最早的已经在栈中的结点。设以 u 为根的子树为 $\textit{Subtree}_u$。$\textit{low}_u$ 定义为以下结点的 $\textit{dfn}$ 的最小值：$\textit{Subtree}_u$ 中的结点；从 $\textit{Subtree}_u$ 通过一条不在搜索树上的边能到达的结点。

性质：

1. 一个结点的子树内结点的 dfn 都大于该结点的 dfn。
2. 从根开始的一条路径上的 dfn 严格递增，low 严格非降。