字符串

0. 阅读前须知

作者这个菜鸡是向 oi.wiki 学的，很容易出现相同的东西。但写的东西，都是我自己理解的。

1. 字符与字符串的存储

什么是字符串呢？就是一堆字符的东西。很容易想到用 char s[MAXN] 定义。

这里介绍一种新的数据结构：string。

如果要定义一堆字符串呢？用 string s[MAXN] 就可以了。

不过给定另一种定义方式——字典树（Trie）

先来看看字典树是怎么定义的。例如这几个字符串：iak，ioi，iakioi，ioiakme。

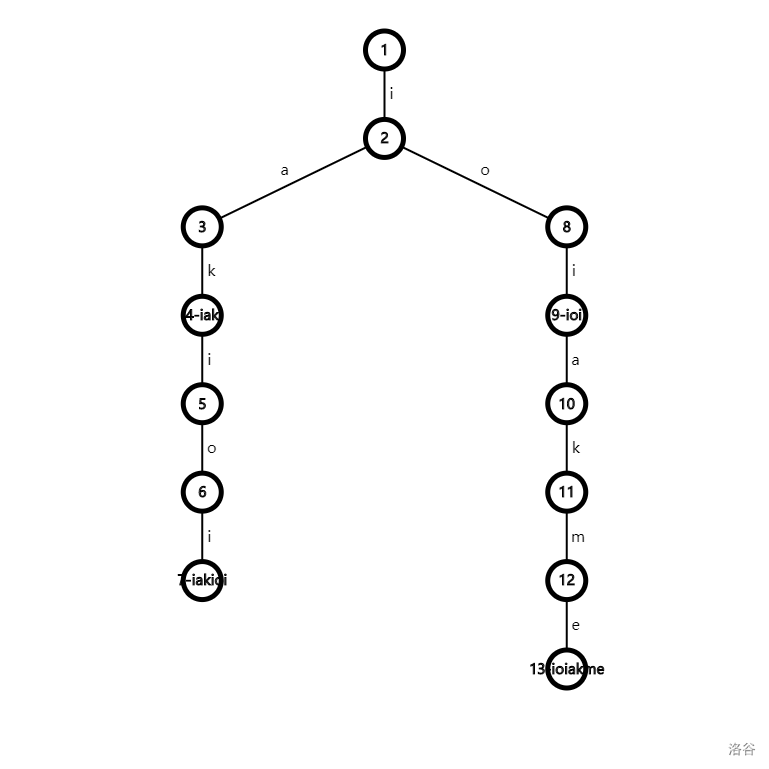
字典树上用边存贮每个字符，用每个简单路径存储每个字符串。如上图。

例如：魔族密码。

字典树的加入：

void insert(string s)
{
	int u=1;//根 
	int len=s.size();
	int res=0;
	for(int i=0;i<len;i++)
	{
		int z=s[i]-'a'+1;
		if(trie[u][z]==0)
			tot++,trie[u][z]=tot;
		u=trie[u][z];
		res+=word[u];
	}
	word[u]++,res++;
	ans=max(res,ans);
}

使用 insert(s) 插入字符串 $s$。

字典树就是这样定义的。

2. KMP

2.1 border

如果一个字符串的前缀等于他的后缀，我们称这个字符串是原字符串的 border。
例如，abcakmeabc 中，abc 就是一个border。

2.2 KMP

定义一个字符串的 $nxt$ 数组表示：前 $i$ 个字符的最长 border 长度。（不为自己）

那 $nxt$ 是干什么的呢？这里直接给出结论：

$nxt$ 是用来回溯的，当模式串和文本串不匹配时，应该从哪来重新开始匹配。

KMP经常用来求解模式串匹配的问题。即询问 $s$ 在 $t$ 中出现的次数。一般来说，代码如下：

j=0;
for(int i=1;i<=m;i++)
{
		while(j>0&&b[j+1]!=a[i])
			j=nxt[j];
		if(b[j+1]==a[i])
			j++;
		if(j==n)
			j=nxt[j];
}

其中，$m=|t|,n=|s|$。

问题是 $nxt$ 怎么获得呢？用自己匹配自己即可。代码如下：

void kmp(int n,string b)
{
      int j=1;
      for(int i=2;i<=n;i++)
      {
          while(j&&b[i]!=b[j]) j=nxt[j];
          if(b[j]==b[i]) j++;//前后缀相同,j往后移动
          nxt[i]=j;
      }
}

时间复杂度 $O(n)$。

3. exKMP/扩展KMP/Z函数

3.1 什么是 Z 函数

注：字符串从 $0$ 开始编号。

什么是 $\text{Z}$ 函数呢？我们定义 $z^i$ 表示 $s$ 与 $s$ 的每一个后缀 $i\sim n-1$ 的最长公共前缀（LCP）的长度，此时我们称 $z$ 为 $s$ 的 $\text{Z}$ 函数。特殊的，$\mathbf{z}[0]=0$。

举几个栗子：

$z($aaaaa$)=[0,4,3,2,1]$；$z($aaabaab$)=[0,2,1,0,2,1,0]$。

3.2 Z 函数线性求法

就像 $nxt$ 一样，Z 函数也可以在 $O(n)$ 复杂度中求。

首先假设已知 $z^0,z^1,\cdots ,z^{i-1}$，现在要求 $z^i$。

如果 $z^i$ 被求出来了，那么 $s[i,i+z^i-1]$ 一定是 $s$ 的前缀，且 $s[i,i+z^i]$ 一定不是 $s$ 的前缀。那么现在正在处理 $z^i$，区间 $s[i,i+z^i-1]$ 就称为我们的匹配段，简称 Z-box。

由于 $\text{LATEX}$ 太难敲了，所以我们简称 $[l,r]$ 是我们的匹配段。由于左端点已知，我们只需要扩展右端点。根据定义，$[l,r]$ 是 $s$ 的前缀。我们维护的时候 $l\le i$，初始 $l=r=0$。

分两种情况讨论

• 当前处理的 $i$ 在 $r$ 的左边（$i\le r$）：由于是匹配段，那么同一长度的 $s$ 肯定是相等的！（因为他们都是 $s$ 的前缀，长度又相等，必然相同）就有性质：$s[i,r]=s[i-l,r-l]$。所以 $z^i=z^{i-l}$？别忘了，$z[i]$ 的长度一定不超过 $r-i+1$（怎么可能超过字符串长度？）所以 $z^i\ge \min \{z^{i-l},r-i+1\}$。
  • 如果 $z^{i-l}<r-i+1$，那么 $z^i=z^{i-l}$。
  • 如果 $z^{i-1}\ge r-i+1$，那么 $z^i=r-i+1$ 的基础上，暴力扩展 $z^i$。
• 如果 $i>r$，暴力扩展

最后，如果 $i+z^i-1>r$，则令 $l=i,r=i+z^i-1$ 即可。

3.3 代码

for(int i=1;i<n;i++)
{
	int len=r-i+1;
	if(i<=r&&z[i-l]<len) z[i]=z[i-l];
	else
	{
		z[i]=max(0ll,len);
		while(i+z[i]<n&&a[z[i]]==b[i+z[i]]) z[i]++;
	}
	if(i+z[i]-1>r) l=i,r=i+z[i]-1;
}

3.4 时空复杂度分析

容易发现，内层 $r$ 每次至少加一，外层 $i$ 每层加一。总的时间复杂度 $O(n)$。

4. Manacher

4.1 反串、回文串

定义一个字符串 $s$ 的反串 $s^r$ 为：

• 长度相等；
• $s[i]=s^r[len-i+1]$。

如果一个串的反串等于他自身，我们称其为回文串。

回文串分为长度为奇数的回文串和长度为偶数的回文串。这是一句废话。

4.2 Manacher 是干嘛的

Manacher，也就是马拉车，可以求出每一对 $l,r$ 使得 $s[l,r]$ 为回文串的 $l,r$。

假设有一个这样的串：

$$\stackrel{aaa\cdots aa}{n\text{个}a}$$

这样的字符串会有 $n^2$ 个回文串，所以马拉车看起来似乎不可能有线性做法。然而，它有。

4.3 Manacher 线性求回文串

考虑一个朴素算法：枚举每个点作为中心，往外扩展。

定义 $p^i$ 表示以点 $i$ 为中心，使得字符串 $s[i-p^i,i+p^i]$ 为回文串而 $s[i-p^i-1,i+p^i+1]$ 不为回文串的回文串半径 $p^i$。

定义 $[l,r]$ 为我们正在处理回文串边界。初始 $l=0,r=-1$。

这个东西很像 Z 函数。那么我们可以得到规律：当 $i>r$ 时，暴力扩展。因为我们无论怎样都不可能使用 $[l,r]$ 得到 $p^i$。

那当 $i\le r$ 时呢？考虑一下怎么从 $[l,r]$ 中得到点信息。首先在 $[l,r]$ 中，$i$ 对应的应该是 $l+r-i$。为什么？

设 $s$ 是 $i$ 所对应的点，依题意得：$i-l=r-s$，经移项，$s=l+r-i$。

那么有一种想法就是：因为 $i$ 对应的是 $s$，那么 $p^i=p^s$。但是这东西不能超过 $r-i+1$，所以 $p^i=\min \{p^s,r-i+1\}$，然后暴力扩展即可。

那这种说法对不对呢？显然是对的。

最后更新 $l=i-p^i+1,r=i+p^i-1$ 即可。

4.4 统一奇偶回文串

回文串分为长度为奇数的回文串和长度为偶数的回文串。这不是一句废话，因为偶回文串会让操作变得很不统一。所以我们在字符的两边都加上一个 |。比如：|a|b|c|d|e|f|g|。

4.5 代码

//这是输入
void qr()
{
	char c=getchar();
	s[0]='~',s[n=1]='|';
	n=1;
	while(c<'a'||c>'z') c=getchar();
	while(c>='a'&&c<='z')
	{
		s[++n]=c,s[++n]='|';
		c=getchar();
	}
}
//这是Manacher
for(int i=1;i<=n;i++)
{
	if(i<=r) p[i]=min(p[l+r-i],r-i+1);//对应点对
	while(s[i-p[i]]==s[i+p[i]]) p[i]++;//暴力扩展
	if(p[i]+i>r) r=i+p[i]-1,l=i-p[i]+1;//更新左右端点
}

4.6 时空复杂度分析

容易发现，内层 $r$ 每次至少加一，外层 $i$ 每层加一。总的时间复杂度 $O(n)$。

5. 自动机

5.1 为什么讲“自动机”

你或许以为我要讲 AC 自动机，实际上我要先说自动机。

前后讲的 trie、kmp、AC自动机、后缀自动机 全部属于自动机。这也是为什么要将“自动机”。

5.2 自动机的形式化定义

那自动机到底是什么呢？你可以把它看成一个有向图。这些图中，有字符集 $\Sigma$、状态集合 $Q$（如初始状态集合 $start$、终止状态集合 $F$）、转移函数 $\delta$。我们把自动机简称为 $\text{DFA}$。

假设有一个 $\text{DFA }A$，如果 $A$ 能接受 $S$，那么 $A(S)=\text{True}$，否则我们说 $A(S)=\text{False}$。

$\text{DFA}$ 的运行过程如下：每次按每一位进行转移，如果读入完所有的字符后进入了一个终止集合，那么我们说 $A$ 能接受 $S$，否则说 $A$ 不能接受 $S$。

如果从状态 $v$ 无法转移 $c$，我们称 $\delta (v,c)=\text{null}$。$\text{null}$ 能也只能转移到 $\text{null}$。

5.3 一些自动机

• Trie：对照定义，会发现这是一个典型的自动机
• KMP：也是自动机
• AC 自动机：都写脸上了还不是自动机？

6. AC 自动机

6.1 AC 自动机是干什么的？

AC 自动机 = KMP 炒鸡版。AC 自动机解决的也是一类匹配问题，但解决的是多模式匹配问题。

一般来说，AC 自动机 = Trie + KMP。推荐你先学完 KMP 和 Trie 后再来看 AC 自动机。

6.2 AC 自动机大体思路

1. 构造所有模式串的 Trie
2. 创建失配指针（即 fail 指针）

6.3 Step1.建立字典树

AC 自动机的第一步就是创建所有模式串的 Trie。AC 自动机建立在 Trie 之上。

容易发现，Trie 的每一个节点都是字符串的前缀（状态）。

6.4 失配指针

失配指针？KMP！

AC 自动机的 fail 指针和 KMP 的 next 指针其实差不多。区别在 KMP 跳转的是最长 border，而 AC 自动机跳转的是所有模式串的前缀中匹配当前状态的最长后缀。

6.5 Step2.求 fail 指针

跟 KMP 简直一模一样。

假设现在我们处理到了节点 $x$，他的父节点是 $f$，满足转移 $\delta (f,k)=x$，即通过字符 $k$ 衔接。

• 如果转移 $\delta ({\mathrm{fail}}^f,k)$ 存在，即有一条路径 ${\mathrm{fail}}^f\to k$，因为 $\delta (f,k)=x$，所以 $\delta ({\mathrm{fail}}^f,k)={\mathrm{fail}}^x$。
• 否则去寻找 $\delta ({\mathrm{fail}}^{{\mathrm{fail}}^f},k)$ 是否存在，就这样一直 $\mathrm{fail}$ 下去。
• 还没有？${\mathrm{fail}}^u=$ 根节点。

考虑怎么实现处理 $\mathrm{fail}$ 指针。把这颗树进行 BFS。定义：

• $\delta (f,k)$，状态 $f$ 经过字符 $k$ 后到达的状态。
• $q$，队列
• ${\mathrm{fail}}^u$，$u$ 的失配指针。

void build()
{
	queue<int>q;
	for(int i=1;i<=26;i++)
		if(a.trie[0][i]) q.push(a.trie[0][i]);
	while(!q.empty())
	{
		int u=q.top();q.pop();
		for(int i=1;i<=26;i++)
			if(tr[u][i])
				fail[tr[u][i]]=tr[fail[u]][i],q.push(tr[u][i]);//oi.wiki修改了
			else
         		tr[u][i]=tr[fail[u]][i];
	}
}

AC 自动机通过修改字典树，将其变成了一张字典图。

6.6 Step3.进行匹配

我们用 $\mathrm{query}$ 函数来进行匹配。代码如下：

int query(string s)
{
	int u=0,ans=0;
	for(int i=0;i<s.size();i++)
	{
		u=tr[u][s[i]-'a'+1];
    	for(int j=u;j&&e[j]!=-1;j=fail[j])
    		ans+=e[j],e[j]=-1;
	}
    return ans;
}

这里我们定义 e[j]=1 表示在编号为 $j$ 的节点上，有一个完整的模式串。

原理很简单：通过 $\mathrm{fail}$ 指针跳转，标记出现模式串记录下来即可。

6.7 AC 自动机的放松小视频

 

 

转自 B 站博主 科研界干饭王。

6.8 例题：AC 自动机（简单版）

就用讲过的 AC 自动机就可以了。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=2000005;
struct Trie{
	int trie[MAXN][30],e[MAXN*30],tot=0;
	void insert(string s)
	{
		int u=0,len=s.size();s=" "+s;int res=0;
		for(int i=1;i<=len;i++)
		{
			int z=s[i]-'a'+1;
			if(trie[u][z]==0) tot++,trie[u][z]=tot;
			u=trie[u][z];
		}
		e[u]++;
	}
};
struct AC{
	Trie a;
	int fail[MAXN*30];
	//略
}tree;
signed main()
{
	int n;cin>>n;
	string s;
	for(int i=1;i<=n;i++)
		cin>>s,tree.a.insert(s);
	tree.build();
	cin>>s;s=" "+s;
	cout<<tree.query(s);
	return 0;
}

6.9 例题：AC 自动机（简单版 II）

考虑记录 fail 跳转的次数即可。

int query(string s)
{
	int u=0,ans=0;
	for(int i=0;i<s.size();i++)
	{
		u=a.trie[u][s[i]-'a'+1];
		for(int j=u;j;j=fail[j])
    	{
			if(a.Id[j]) a.e[j]++;
		}
	}
	for(int i=1;i<=n;i++) ans=max(ans,a.e[a.id[i]]);
	return ans;
}

6.10 例题：【模板】AC 自动机/AC 自动机的优化

哇，好像比简单版II还水！然后 T 了。

为什么会 T 呢？我们发现 fail 指针跳的时候，有大量的重复计算。

我们发现 fail 指针不会出现环，那么 fail 边一定会构成一颗树。那么 AC 自动机的匹配其实就是求一条链的长度。考虑一下怎么优化。

有两种优化方式，拓扑排序和子树求和。

• 拓扑排序
  首先建立一颗 fail 树。容易想到，有一条边是 $u-{\mathrm{fail}}^u$。然后先为 $s$ 所在的状态打上标记。

void query(string s)
{
	int u=0;
	for(int i=0;i<s.size();i++)
	{
		u=a.trie[u][s[i]-'a'+1];
        e[u]++;
	}
}

最后用一个拓扑排序求出答案。

• 子树求和
  求出每颗子树的和即可。