线段树（合集）

0. 树？睡蕉小猴！

因为以前的线段树写成了好几个 blog，所以这里写一个合集。

1. 线段树

1.1 线段树 1

线段树是用来处理一类“区间修改+区间操作”的问题的数据结构。

1.2 线段树的节点与性质

建立一棵二叉树，根节点为 $1$ ，每个节点会处理一个区间 $[l,r]$ 的和，比如根节点会处理 $[1,n]$ 。

由二叉树，我们知道节点 $u$ 的两个儿子是 $2u$ 和 $2u+1$ 。

定义 $w_u=\sum \limits_{w_{u对应的l}}^{u对应的 r}a_i$ 。

规定：若 $u$ 对应的区间为 $[l,r]$ （以下不再写“对应的区间”），定义 $mid=\left\lfloor\dfrac{l+r}{2}\right\rfloor$ ，则 $2u$ 对应区间 $[l,mid]$ ， $2u+1$ 对应区间 $[mid+1,r]$ 。

定义： $u$ 是叶子节点。

那么线段树到底长成了什么样子呢？如图：

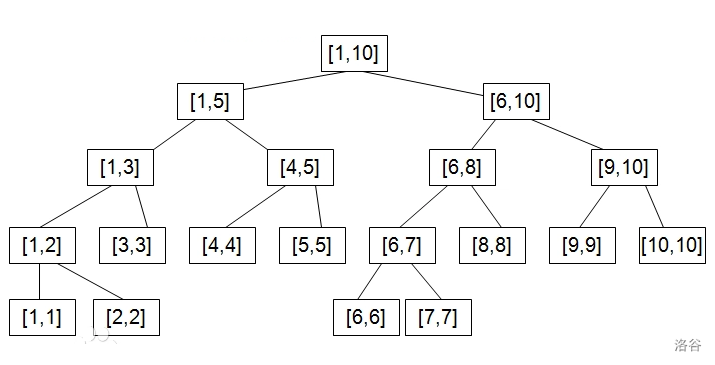
观察线段树：

每个点要么有 $2$ 个子结点，有么为根。
有 $2n-1$ 个节点。
高为 $\log n$ 。

1.3 建立一颗线段树

有一个显然的性质， $w_u=w_{2u}+w_{2u+1}$ 。

那么定义合并函数 pushup(int u)：

void pushup(int u)
{
  w[u]=w[u*2]+w[u*2+1];
}

那怎么对于一个序列 $a$ 建立一颗线段树呢？直接上代码：

void build(int u,int l,int r)
{
  if(l==r)
  {
    w[u]=a[l];
    return;
  }
  int mid=(l+r)/2;
  build(u*2,l,mid);
  build(u*2+1,mid+1,r);
  pushup(u);
}

代码很好理解。

1.4 区间查询

我们知道查询区间为 $[l,r]$ 。我们可以想到，如果 $[L,R]$ 属于 $[l,r]$ ，则直接返回当前区间和。如果完全没有交集，可以直接返回 $0$ 。不然，分成两部分去查找。

代码如下：

bool InRange(int L,int R,int l,int r)
{
  return (l<=L)&&(R<=r);
}
bool OutofRange(int L,int R,int l,int r)
{
  return (L>r)||(R<l);
}
long long query(int u,int L,int R,int L,int r)
{
  if(InRange(L,R,l,r)) return w[u];
  else if(!OutofRange(L,R,l,r))
  {
    int m=(L+R)/2;
    return query(u*2,L,m,l,r)+query(u*2+1,m+1,R,l,r);
  }
  else return 0;
}

1.5 懒标记与区间查询

定义：懒标记（ $\text{lazy\_tag}$ ）是用来记录区间修改的信息的一个标记，比如下面这个例子：

一个班的学习委员知道语文作业后，不用立即告诉下面的组长们，可以再等一下数学作业。（修改时不直接下方标记）
懒标记具有可合并性，比如语文 $1$ 张试卷，数学 $1$ 张试卷，那么总共 $1+1=2$ 张试卷。
如果老师问学习委员作业写完没有，只需要自己写完即可。（不涉及叶子节点不下方标记）
知道所有作业后也不需要立刻告诉大家，老师收作业时再告诉大家即可。（查询叶子节点下方懒标记）

那么区间修改和区间查询可以这么写：

void maketag(int u,int len,long long x)
{
  lzy[u]+=x;
  w[u]+=len*x;
}
void pushdown(int u,int l,int r)
{
  int m=(l+r)/2;
  maketag(u*2,m-l+1,lzy[u]);
  maketag(u*2+1,r-m,lzy[u]);
  lzy[u]=0;
}
void update(int u,int L,int R,int l,int r,long long x)
{
  if(InRange(L,R,l,r)) maketag(u,R-L+1,x);
  else if(!OutofRange(L,R,l,r))
  {
    int m=(L+R)/2;
    pushdown(u,L,R);
    update(u*2,L,m,l,r,x);
    update(u*2+1,m+1,R,l,r,x);
    pushup(u);
  }
}
long long query(int u,int L,int R,int l,int r)
{
  if(InRange(L,R,l,r)) return w[u];
  else if(!OutofRange(L,R,l,r))
  {
    int m=(L+R)/2;
    pushdown(u,L,R);
    return query(u*2,L,m,l,r)+query(u*2+1,m+1,R,l,r);
  }
  else return 0;
}

1.6 封装线段树

初学阶段千万不要复制，等你自己能在至多 $10\text{min}$ 把线段树默写出来再复制。

const int maxn=500006;//依情况修改
struct Segment{//依情况修改
	long long a[maxn],w[4*maxn],lzy[4*maxn];
	void pushup(int u)
	{
		w[u]=w[u*2]+w[u*2+1];
	}
	void build(int u=1,int l=1,int r=n)
	{
		if(l==r)
		{
			w[u]=a[l];
			return;
		}
		int m=(l+r)/2;
		build(u*2,l,m),build(u*2+1,m+1,r);
			pushup(u);
	}
	bool InRange(int L,int R,int l,int r)
	{
		return (l<=L)&&(R<=r);
	}
	bool OutofRange(int L,int R,int l,int r)
	{
		return (L>r)||(R<l);
	}
	void maketag(int u,int len,long long x)
	{
		lzy[u]+=x;
		w[u]+=len*x;
	}
	void pushdown(int u,int l,int r)
	{
		int m=(l+r)/2;
		maketag(u*2,m-l+1,lzy[u]);
		maketag(u*2+1,r-m,lzy[u]);
		lzy[u]=0;
	}
	int query(int l,int r,int u=1,int L=1,int R=n)
	{
		if(InRange(L,R,l,r)) return w[u];
		else if(!OutofRange(L,R,l,r))
		{
		  int m=(L+R)/2;
		  pushdown(u,L,R);
	  	return query(l,r,u*2,L,m)+query(l,r,u*2+1,m+1,R);
		}
		else return 0;
	}
	void update(int l,int r,long long x,int u=1,int L=1,int R=n)
	{
		if(InRange(L,R,l,r)) maketag(u,R-L+1,x);
		else if(!OutofRange(L,R,l,r))
		{
			int m=(L+R)/2;
			pushdown(u,L,R);
			update(l,r,x,u*2,L,m);
			update(l,r,x,u*2+1,m+1,R);
			pushup(u);
		}
	}
};

定义：Segment a;

使用：构造 a.build()，区间修改 a.update(x,y,k)，区间查询 a.query(x,y)。其中， $x,y$ 为区间， $k$ 为修改值。注意有些函数的值顺序改了一下，记得调回来。此份代码是求区间和的代码。

1.7 开关

这里很简单，区间异或就是将 $0$ 和 $1$ 互换。所以稍微变动一下 $\text{maketag}$ 函数便可：

void maketag(int u,int len,long long x)
{
		lzy[u]^=1;
		w[u]=len-w[u];
}

1.8 线段树适用范围

可以发现，线段树一定可以从 $w_{2u}$ 和 $w_{2u+1}$ 转化而来，也就是满足“分配率”。

比如区间众数便不能由线段树维护。而区间异或，区间 GCD 都可以用线段树维护。

1.9 线段树 2/多标记处理

这题需要建立两个标记：加法标记和乘法标记。

这时候需要注意标记下方顺序。

详见此题题解。

1.10 复杂度分析

空间复杂度 $O(4n)$ 。

时间复杂度：建树 $O(n)$ ，单次操作 $O(\log n)$ 。

2. 动态开点线段树

这是线段树最简单的拓展。

请在理解完线段树后再来看此节。

2.1 适用范围

当操作区间很大（ $[1,10^9]$ ）甚至出现负数（ $[-10^9,10^9]$ ）的时候，就需要用到动态开点线段树。

2.2 动态开点的本质

观察线段树，单次操作最多使用的点为 $\log n$ 的。

那么实际上整棵树最多使用的点为 $q\log n$ 的。

一般来说， $n\le 10^9$ ，那么 $\log n=30$ 左右。

所以动态开点只记录这些节点，最多只需要开 $O(30q)$ 的节点个数左右。一般来说还需要加一点。

2.3 动态开点的实现 / 封装动态开点线段树

用一个 node 存储数据：

struct node{
	int l,r,val,lzy;
	node(){
		l=r=val=lzy=0;
	}
}tr[30*maxm];

pushdown 操作时，除了更新 $\text{lazy\_tag}$ ，还要开新节点。

void pushdown(int u,int l,int r)
{
	if(!tr[u].l) tr[u].l=++tot;
	if(!tr[u].r) tr[u].r=++tot;
	int mid=(l+r)/2;
	maketag(tr[u].l,mid-l+1,tr[u].lzy);
	maketag(tr[u].r,r-mid,tr[u].lzy);
	tr[u].lzy=0;
}

初始时只需要开一个根节点即可。其余操作类似。

#define maxm 500005
int n=2000000000;
struct dt_Segment_tree{
	struct node{
		int l,r,val,lzy;
		node(){
			l=r=val=lzy=0;
		}
	}tr[30*maxm];
	int tot=0;
	dt_Segment_tree(){
		tot++;
	}
	void pushup(int u)
	{
		tr[u].val=tr[tr[u].l].val+tr[tr[u].r].val;
	}
	void maketag(int u,int len,int x)
	{
		tr[u].lzy+=x;
		tr[u].val+=len*x;
	}
	void pushdown(int u,int l,int r)
	{
		if(!tr[u].l) tr[u].l=++tot;
		if(!tr[u].r) tr[u].r=++tot;
		int mid=(l+r)/2;
		maketag(tr[u].l,mid-l+1,tr[u].lzy);
		maketag(tr[u].r,r-mid,tr[u].lzy);
		tr[u].lzy=0;
	}
	bool InRangeOf(int L,int R,int l,int r)
	{
		return (l<=L)&&(R<=r);
	}
	bool OutRangeOf(int L,int R,int l,int r)
	{
		return (L>r)||(R<l);
	}
	void update(int l,int r,int x,int u=1,int L=1,int R=n)
	{
		if(InRangeOf(L,R,l,r)) maketag(u,R-L+1,x);
		else if(!OutRangeOf(L,R,l,r))
		{
			pushdown(u,L,R);
			int mid=(L+R)>>1;
			update(l,r,x,tr[u].l,L,mid);
			update(l,r,x,tr[u].r,mid+1,R);
			pushup(u);
		}
	}
	int query(int l,int r,int u=1,int L=1,int R=n)
	{
		if(InRangeOf(L,R,l,r)) return tr[u].val;
		else if(!OutRangeOf(L,R,l,r))
		{
			pushdown(u,L,R);
			int mid=(L+R)>>1;
			return query(l,r,tr[u].l,L,mid)+query(l,r,tr[u].r,mid+1,R);
		}
		else return 0;
	}
}a;

2.4 【模板】动态开点线段树

模板题，没什么说的。

3. 树套树

阅读本章前请先完成【模板】动态开点线段树。

3.1 什么是树套树

考虑这样一个问题：

在一个 $n\times n$ 的平面上，维护任意一个平面 $(x_1,y_1)\sim(x_2,y_2)$ 的区间覆盖与区间查询。

这题不可以简单的二维树状数组，必须使用线段树。

3.2 线段树套线段树

最简单的树套树。

有一个暴力的想法：我们对于每一行开一个线段树。这样单次操作时间复杂度 $O(n\log n)$ 。

那怎么优化呢？容易发现，对于每一行，我们也可以看成区间加。

那么建一颗线段树，每个线段树的结点都是一颗线段树，那么时间复杂度 $O(\log^2n)$ 。

但是如果直接这么建是 $O(4n\times 4n)=O(16n^2)$ 的，不仅常数大，而且 $O(n^2)$ 的空间复杂度可以 XXX 了。

考虑动态开点，这样每一次只会增加 $O(\log^2n)$ 个结点。

空间时间复杂度就都是 $O(q\log^2 n)$ 的了，非常优秀。

4. 可持久化线段树

5. 扫描线

posted @ 2024-11-13 10:25 sLMxf 阅读(49) 评论(0) 收藏举报来源

刷新页面返回顶部

SLMXF

死了吗小枫？