函数方程思想

高中数学热门技巧——方程思想

定点在曲线问题

例题 1

题目

已知椭圆方程 \(\dfrac{x^2}{4}+y^2=1\)，设直线 \(l\) ，不经过点 \(P(0,1)\)且与椭圆相交于 \(A,B\) 两点，若直线 \(PA\) 与直线 \(PB\) 的斜率和为 \(-1\) ，证明：直线 \(l\) 过定点。

题解

由直线 \(l\) 不过点 \(P(0,1)\) 可设直线 \(l\) 方程： \(mx+n(y-1)=1\) 。
设点 \(A(x_1,y_1),B(x_2,y_2)\) 。
由点 \(A\) 在椭圆上可得：

\[{x_1}^2+4{y_1}^2=4 \\ \\ \Downarrow \\ 4[(y_1 -1)+1]^2+{x_1}^2 =4 \]

展开后得：

\[4(y_1 -1)^2+8(y_1 -1)+4+{x_1}^2=4 \\ \Downarrow \\ 4(y_1 -1)^2+8(y_1 -1)[mx_1+n(y_1 -1)]+4+{x_1}^2=4 \\ \Downarrow \\ (4+8n)(y_1 -1)^2+8mx_1(y_1-1)+{x_1}^2=0 \]

等式两边同时除以 \({x_1}^2\) 得：

\[(4+8n) (\dfrac{y_1-1}{x_1})^2+8m\dfrac{y_1-1}{x_1}+1=0 \\ \Downarrow \\ (4+8n){k_{PA}}^2+8mk_{PA}+1=0 \]

同理可得：

\[(4+8n){k_{PB}}^2+8mk_{PB}+1=0 \]

可得 \(k_{PA},k_{PB}\) 是方程 \((4+8n)k^2+8mk+1=0\) 的两个根.
\(\Delta>0,4+8n\ne 0 \Rightarrow (8m)^2-4(4+8n)>0\Rightarrow 4m^2>2n+1,n\ne -\dfrac{1}{2}\)
由韦达定理可得：\(k_1+k_2=-\dfrac{8m}{4+8n}=-1\Rightarrow m=n+\dfrac{1}{2}\)
所以 \(l:mx+n(y-1)=1\) 为 \(mx+(\dfrac{1}{2}-m)(y-1)=1\)
可得：

\[n(x+y-1)+\dfrac{1}{2}x=1 \]

当直线 \(l\) 过定点时，满足：

\[\begin{cases}x+y-1=0 \\ \dfrac{1}{2}x=1\end{cases} \]

解得：

\[\begin{cases}x=2\\ y=-1\end{cases} \]

所以直线 \(l\) 过定点 \((2,-1)\).

综上： 直线 \(l\) 过定点 \((2,-1)\)

来源

2017 年全国 I 卷理科第 20 题第 ii 问

切线问题

例题 1

题目

已知椭圆 \(C:\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\) ，若动点 \(P(x_0,y_0)\) 为椭圆外一点，且过点 \(P\) 作椭圆的两条切线相互垂直，求点 \(P\) 的轨迹方程.

题解

当切线斜率不存在时， \({x_0}^2+{y_0}^2=9+4=13\) ，所以点 \(P\) 的轨迹方程为 \({x_0}^2+{y_0}^2=9+4=13\).
当切线斜率存在时，不妨设切线斜率为 \(y=kx+m\) ，因为切线过点 \(P(x_0,y_0)\) ，所以可知 \(m=y_0-kx_0\). 直线与椭圆联立方程可得：

\[\begin{cases}y=kx+m \\ \dfrac{x^2}{9}+\dfrac{y^2}{4}=1 \end{cases}\Rightarrow (9k^2+4)x^2+18kmx+9m^2-36=0 \]

直线与椭圆相切可得： \(\Delta=0\) 即 \(9k^2+4-m^2=0\)
将 \(m=y_0-kx_0\) 带入可得：

\[(9-{x_0}^2)k^2+2x_0y_0k+4-{y_0}^2=0 \]

由题意得两条切线互相垂直，由韦达定理可得： \(\dfrac{4-{y_0}^2}{9-{x_0}^2}=-1\) 即 \({x_0}^2+{y_0}^2=9+4=13\). 所以点 \(P\) 的轨迹方程为 \({x_0}^2+{y_0}^2=9+4=13\).

综上，点 \(P\) 的轨迹方程为 \({x_0}^2+{y_0}^2=9+4=13\).

来源

2014 年广东高考理科第 20 题第 ii 问

例题 2

题目

设 \(P\) 为抛物线 \(C_1:x^2=y\) 上的动点，过点 \(P\) 作圆 \(C_2:x^2+(y+3)^2=1\) 的两条切线，交直线 \(l:y=-3\) 于 \(A,B\) 两点. 是否存在点 \(P\) ，使线段 \(AB\) 被抛物线 \(C_1\) 在点 \(P\) 处的切线平分，若存在，求出点 \(P\) 的坐标；若不存在，请说明理由.

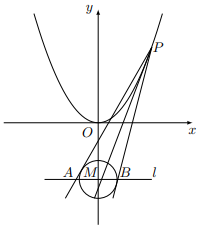
题解

不妨设点 \(P(x_0,{x_0}^2)\ (x_0\ne 0)\) ，可得过点 \(P\) 的切线方程为 \(xx_0=\dfrac{y}{2}+\dfrac{{x_0}^2}{2}\) ，其与
直线 \(y=-3\) 相交，设其交点为 \(D\) ,可解得： \(D(\dfrac{{x_0}^2-3}{2x_0},-3)\) .
设过点 \(P\) 与圆 \(C_2\) 相切的直线为 \(l:x=my+t\) ，其中 \(t=-m{x_0}^2+x_0\) ，由题意得直线 \(l\) 与圆 \(C_2\) 相切，则：

\[\dfrac{|3m-t|}{\sqrt{1+m^2}}=1 \Rightarrow 8m^2-6mt+t^2-1=0 \]

将 \(t=-m{x_0}^2+x_0\) 带入可得：

\[({x_0}^4+6{x_0}^2+8)m-2x_0({x_0}^2+3)m+{x_0}^2-1=0 \]

由韦达定理可得：

\[m_1+m_2=\dfrac{2x_0({x_0}^2+3)}{{x_0}^4+6{x_0}^2+8}\ m_1m_2=\dfrac{{x_0}^2-1}{{x_0}^4+6{x_0}^2+8} \]

直线 \(l\) 与 直线 \(y=-3\) 联立可得： \(x=-m(3+{x_0}^2)+x_0\) 所以 \(x_A=x=-m_1(3+{x_0}^2)+x_0,x_B=x=-m_2(3+{x_0}^2)+x_0\) 所以 \(x_A+x_B=-(m_1+m_2)(3+{x_0}^2)+2x_0=-\dfrac{2x_0}{{x_0}^4+6{x_0}^2+8}\)
由题点 \(D\) 为线段 \(AB\) 的中点可得： \(x_A+x_B=2x_D\) 可得

\[-\dfrac{2x_0}{{x_0}^4+6{x_0}^2+8}=2\left(\dfrac{{x_0}^2-3}{2x_0}\right) \]

化简可得：

\[{x_0}^6+3{x_0}^4-8{x_0}^2-24=0\Rightarrow ({x_0}^2-2\sqrt 2)({x_0}^4+(3+2\sqrt 2){x_0}^2+6\sqrt 2)=0 \]

易得 \({x_0}^4+(3+2\sqrt 2){x_0}^2+6\sqrt 2=0\) 无实数根，所以 \(x_0=\pm\sqrt[4]8\)，所以 \(P(\pm\sqrt[4]8,2\sqrt 2)\).

综上：

点 \(P\) 的坐标为 \(P(\pm\sqrt[4]8,2\sqrt 2)\).

来源

2011 年浙江高考文科第 22 题第 ii 问

例题 3

题目

已知抛物线 \(C_1:x^2=y\) ，圆 \(C_2:x^2+(y-4)^2=1\) 的圆心为点 \(M\) . 已知点 \(P\) 是抛物线 \(C_1\) 上的一点（异于原点），过点 \(P\) 作圆 \(C_2\) 的两条切线，交抛物线 \(C_1\) 于 \(A,B\) 两点，若过 \(M,P\) 两点的直线 \(l\) 垂直于 \(AB\) ，求直线 \(l\) 的方程.

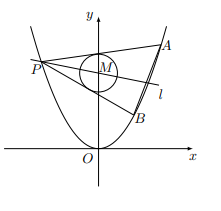
题解

设点 \(P(x_0,y_0)\) ，且切线的斜率为 \(k\) ，则切线的方程为 \(y=k(x-x_0)^2+x_0\) ，直线 \(l\) 斜率 \(k_{MP}=\dfrac{{x_0}^2-4}{x_0}\) ，因为该直线与圆相切，所以：

\[\dfrac{|4+kx_0-{x_0}^2|}{\sqrt{1+k^2}}=1 \Rightarrow ({x_0}^2-1)k^2+2x_0(4-{x_0}^2)k+(4-{x_0}^2)^2-1=0 \]

不妨设直线 \(PA\) 和 \(PB\) 的斜率分别为 \(k_1,k_2\) ，由韦达定理可得：

\[k_1+k_2=-\dfrac{2x_0(4-{x_0^2})}{{x_0}^2-1},\ \ \ k_1k_2=\dfrac{(4-{x_0}^2)^2-1}{{x_0}^2}-1 \]

将抛物线 \(C_1\) 与切线方程（ 注意这里不是直线 \(l\) ）联立：

\[\begin{cases}y=x^2 \\ y=k(x-x_0)+{x_0}^2\end{cases} \Rightarrow x^2-kx+kx_0-{x_0}^2=0 \]

已知 \(P(x_0,y_0)\) 为其中一根，所以另一根为 \(k-x_0\) ，已知直线 \(PA,PB\) 的斜率分别为 \(k_1,k_2\) 可得 \(x_A=k_1-x_0,x_B=k_2-x_0\) ，由于点 \(A,B\) 都是在抛物线上的，可求得

\[A(k_1-x_0,(k_1-x_0)^2),\ \ \ B(k_2-x_0,(k_2-x_0)^2) \]

所以可求得直线 \(AB\) 的斜率为

\[k_{AB}=\dfrac{y_B-y_A}{x_B-x_A}=-\dfrac{2x_0(4-{x_0}^2)}{{x_0}^2-1}-2x_0 \]

因为 \(l\perp AB\) ，所以

\[k_{AB}k_{MP}=-1\Rightarrow \left[-\dfrac{2x_0(4-{x_0}^2)}{{x_0}^2-1}-2x_0\right]k_{MP}=\dfrac{{x_0}^2-4}{x_0}=-1 \Rightarrow {x_0}^2=\dfrac{23}{5} \]

所以 \(P(\pm\sqrt{\dfrac{23}{5}},\dfrac{23}{5}),k_{PM}=\pm\dfrac{3\sqrt{115}}{115}\) ，所以直线 \(l\) 的方程为 \(y=\pm\dfrac{3\sqrt{115}}{115}x+4\)

综上，直线 \(l\) 的方程为：

\[y=\pm\dfrac{3\sqrt{115}}{115}x+4 \]

来源

2011 年浙江高考理科第 21 题第 ii 问