『图的连通性进阶』 知识点 总结

前言

若有长风绕旗，那便是我在想你了。

这周讲了个图论连通性板块的一些进阶知识，周六全国第一给我们讲了一些树上的问题，感觉树剖板块实现难度较大，后面几道偏思维的题会有些许好转。

这里就先写写连通性相关的进阶的一些知识点吧。

主要涵盖：耳分解，双极定向，三连通分量和一些重要的结论。

（其实我不会告诉你大部分都是我抄的 \(\text{2023}\) 年的集训队论文。）

建议先理解透彻双连通分量以及圆方树的相关知识和求法再来进阶，不然就会像我一样，调半天的三连通分量，因为下面这张图：

耳分解

\(\large \mathbf{Difinition \ 1}\)

我们有如下对于耳，开耳的定义：

在无向图 \(G=(V,E)\) 中，有一个子图 \(G'=(V',E')\)，若存在简单路径或者简单环 \(P:x_1\to x_2\to x_3.....\to x_t\)，满足 \(x_1,x_t\in V',\forall i\in [2,t-1],x_i\not\in V'\)，则称 \(P\) 是 \(G\) 中关于 \(G'\) 的耳，如果 \(P\) 是简单路径，那么则称 \(P\) 是 \(G\) 关于 \(G'\) 的开耳。

\(\large \mathbf{Difinition\ 2}\)

我们再给耳分解下一个定义。

对于无向连通图 \(G=(V,E)\)，有一个连通子图序列 \((G_0,G_1,....G_k)\)，满足以下条件：

• \(G_0\) 是一个简单环（一个点也是可以的），以及 \(G_k=G\)。
• \(\forall i\in [1,k]\)，\(G_{i-1}\) 是 \(G_i\) 的子图。
• 如 \(G_i=(V_i,E_i)\)，那么 \(E_i \setminus E_{i-1}\) 就是 \(G\) 中关于 \(G_{i-1}\) 的耳。

满足上述条件的连通子图序列，就称为 \(G\) 的一个耳分解。

当然，这里的耳分解将里面所有的耳换成开耳就可以得到开耳分解的定义。

\(\large \mathbf{Theory\ 1}\)

无向连通图 \(G=(V,E)\) 中存在耳分解当且仅当图 \(G\) 边双连通。

相当于两者之间是个充要条件的关系，故我们分步证明。

先证必要性，即 \(G\) 存在耳分解 \(\to\) \(G\) 边双连通：

• 假设 \(G\) 的耳分解是 \((G_0,G_1,....,G_k)\)。根据定义，\(G_0\) 显然边双连通，而在 \(G_i\) 边双连通时，对于 \(G_{i+1}\) 的加入，可以发现 \(E_{i+1}\) 内部显然不可能存在一条割边（因为你总是能从两个方向中的一个到达这个点），故 \(G_{i+1}\) 也满足边双连通，然后根据数学归纳法，\(G=G_k\) 边双连通。

再证充分性，即 \(G\) 边双连通 \(\to\) \(G\) 存在耳分解：

• 首先，如果 \(|E|=0\)，那么显然 \(|V|=1\)，显然成立。
• 否则，先以 \(1\) 为根，搞出图 \(G\) 的一颗搜索树，然后按照如下方式构造耳分解：
• 第一步，由于这个图是边双联通的，故我们一定可以找到一条非树边 \(1\to x\)，那么这条边就会和 \(1\sim x\) 这条路径构成一个简单环，我们钦定这个简单环就是我们要构造的 \(G_0\)。
• 第二步，假设现在已经生成了连通子图的序列 \(G_i\)，如果 \(G_i\) 的点集 \(V_i\not= V\)，找到一个点 \(x\) 满足 \(x\notin V_i \ \wedge\) \(x\) 在搜索树上的父亲 \(y\in V_i\)。仍然通过边双连通的性质，我们一定可以找到一条路径 \((u,v)\) 满足 \(u\) 是 \(y\) 的祖先，\(v\) 是 \(x\) 的后代，可以发现，\(v\to u\) 这条边和 \(y\sim v\) 这条路径，就会构成一个新的耳，且至少含有一个新点 \(x\)，令 \(G_{i+1}\) 表示 \(G_i\) 加上这个耳。（可以发现，由于 \(G_i\) 一直是一个包含了根节点的联通块，所以在 \(V_i\not= V\) 时，这样的 \(x\) 显然是一直存在的。
• 第三步，我们在 \(V_i\not= V\) 的时候持续进行第二步，必然只会在最后 \(V_i=V\) 时终止。可能这个时候边集还 \(\not= E_i\)，可以发现未加入的每条边和他的两个端点会分别构成一些耳，然后依次往 \(V_i\) 里面放入即可。

于是证毕。

\(\large \mathbf{Theory\ 2}\)

至少含有三个点的无自环无向连通图 \(G=(V,E)\) 存在开耳分解当且仅当 \(G\) 点双连通。

考虑类比我们刚刚对于第一条定理的证明。

先证必要性，即 \(G\) 存在耳分解 \(\to\) \(G\) 点双连通：

• 假设 \(G\) 的耳分解是 \((G_0,G_1,....,G_k)\)。根据定义，\(G_0\) 显然点双连通，而在 \(G_i\) 点双连通时，对于 \(G_{i+1}\) 的加入，可以发现 \(V_{i+1}\) 内部显然不可能存在一个割点（因为新加入的耳的点数 \(\ge 2\)），故 \(G_{i+1}\) 也满足点双连通，然后根据数学归纳法，\(G=G_k\) 点双连通。

再证充分性，即 \(G\) 点双连通 \(\to\) \(G\) 存在耳分解：

• 不需要考虑 \(|V| \le 2\) 的情况。先以 \(1\) 为根，搞出图 \(G\) 的一颗搜索树，然后按照如下方式构造耳分解：
• 第一步，由于这个图是边双联通的，故我们一定可以找到一条非树边 \(1\to x\)，那么这条边就会和 \(1\sim x\) 这条路径构成一个简单环，我们钦定这个简单环就是我们要构造的 \(G_0\)。
• 第二步，假设现在已经生成了连通子图的序列 \(G_i\)，如果 \(G_i\) 的点集 \(V_i\not= V\)，找到一个点 \(x\) 满足 \(x\notin V_i \ \wedge\) \(x\) 在搜索树上的父亲 \(y\in V_i\)。仍然通过点双连通的性质，我们一定可以找到一条路径 \((u,v)\) 满足 \(u\) 是 \(y\) 的父亲的祖先，\(v\) 是 \(x\) 的后代，可以发现，\(v\to u\) 这条边和 \(y\sim v\) 这条路径，就会构成一个新的开耳，且至少含有一个新点 \(x\)，令 \(G_{i+1}\) 表示 \(G_i\) 加上这个开耳。（可以发现，由于 \(G_i\) 一直是一个包含了根节点的联通块，所以在 \(V_i\not= V\) 时，这样的 \(x\) 显然是一直存在的。
• 第三步，我们在 \(V_i\not= V\) 的时候持续进行第二步，必然只会在最后 \(V_i=V\) 时终止。可能这个时候边集还 \(\not= E_i\)，可以发现未加入的每条边和他的两个端点会分别构成一些开耳，然后依次往 \(V_i\) 里面放入即可。（因为没有自环，所以一定是开耳。）

双极定向

\(\large \mathbf{Theory\ 3}\)

给定无向图 \(G=(V,E)\) 和不同的两个节点 \(s,t\)，以下四个命题等价：

1. 在添加无向边 \((s,t)\) 后，\(G\) 点双连通。
2. \(G\) 的圆方树中所有方点构成一条链，\(s\sim t\) 时圆方树的一条直径。
3. 存在一种对 \(G\) 的边进行定向的方法，得到一个有向无环图，且 \(s\) 入度为 \(0\)，\(t\) 的出度为 \(0\)，其余点出入度都不为 \(0\)。
4. 存在一个所有点的排列 \(p_1,p_2,....,p_n\)，使得 \(p_1=s,p_n=t\) 且任意前缀和任意后缀的导出子图都是联通的。

证明方法是，先证 \(1,2\) 等价，再证 \(3,4\) 等价，再证 \(1\to 3\) 和 \(4\to 1\)

• 先证 \(1,2\) 等价。发现在加入 \((s,t)\) 本质上就是在圆方树上加入了 \(s\to t\) 的一条边，而新构成的圆方树本质上就是加入这条边之后，把这条边对应的两个端点在园方树上的路径上的所有方点代表的连通块缩成一个连通块，而要满足整个图双连通，显然所有方点必须构成一条整链才行。这样才有可能通过一条边缩成同一个连通块。

• 再证 \(3,4\) 等价。如果 \(3\) 成立，那么可以发现，任意一种定向后的拓扑排序就可以构成 \(4\) 中我们想要的排列 \(p\)。可以发现，这样构造出来的 \(p\)，满足 \(\forall i\in [2,n]\)，一定存在一个后继与 \(p_1,p_2,...p_{i-1}\) 中。于是，如果 \(p_1,p_2,...p_{i-1}\) 的导出子图联通，那么 \(p_1,p_2,...p_i\) 的导出子图依然联通，归纳法即证，后缀的证明方法同理。如果 \(4\) 成立，在图中 \(G\) 的定向方法就是让 \(p\) 中靠前的连向 \(p\) 中靠后的点，由于前后缀一定联通，所以显然满足 \(3\) 的条件。

• 接着证 \(1\to 3\)。连完 \((s,t)\) 之后，我们考虑先求出 \(G\) 的开耳分解 \((G_0,G_1,...G_k)\)，满足 \((s,t)\) 在 \(G_0\) 对应的边集中。（构造方法仿照定理 \(2\) 中证明充分性时的构造方法，可以把 \(s\) 看作根，然后强行钦定 \((s,t)\) 为非树边即可做到。）由于 \(G_0\) 必然是个简单环（因为是点双），考虑将 \((s,t)\) 之外的边全部定向为 \(s\to t\) 这个方向，然后考虑归纳法。如果 \(G_i\) 已经在满足 \(3\) 的情况下定向完毕，设在向后分解到 \(G_{i+1}\) 所加入的开耳是一条从 \(u\sim v\) 的简单路径，如果发现在 \(G_i\) 的定向中，\(u\) 可以到达 \(v\)，那么就让开耳的路径定向为 \(u\to v\)，否则就是 \(v\to u\)。可以发现，这样构造出来的 \(G_{i+1}\) 必然不存在环，并且除了 \(s,t\)，其他的点都有出入度，因此最终构造出来的 \(G_k=G\) 时，我们也就同时满足了 \(3\) 的要求。

• 最后证 \(4\to 1\)。考虑反证，如果推不出来 \(1\)，也就是 \(1\) 不成立，在加入边之后 \((s,t)\) 之后，必然存在一个割点 \(u\)，使得 \(s,t\) 在同一连通块，以及至少另外一个连通块 \(S\)。设 \(S\cup \{u\}\) 在 \(p\) 中最早出现的点是 \(x\)，最晚出现的点是 \(y\)，显然 \(x,y\) 至少有一个不是 \(u\)，不妨设 \(x\not= u\)，可以发现，对于 \(p_1,...p_i=x\) 的导出子图，由于 \(u\) 是割点而 \(s,x\) 都在这个子图中，故这个子图不连通，与 \(4\) 矛盾。故得证。

综上所述，证得四个条件是等价的，并且我们得到了 \(1\to 3,4\) 的构造。

边三连通分量

\(\large \mathbf{Difinition \ 3}\)

对于一张无向图 \(G = (V, E)\)。

• 我们称两个点 \(u, v ~ (u, v \in V, u \neq v)\) 是边三连通的，当且仅当存在三条从 \(u\) 出发到达 \(v\) 的，相互没有公共边的路径。

• 我们称一个点集 \(U ~ (U \subseteq V)\) 是边三连通分量，当且仅当对于任意两个点 \(u', v' ~ (u', v' \in U, u' \neq v')\) 都是边三连通的。

• 我们称一个边三连通分量 \(S\) 是极大边三连通分量，当且仅当不存在 \(u \not \in S\) 且 \(u \in V\)，使得 \(S \cup \{u\}\) 也是边三连通分量。

对其的求解方法，更多的是一些技巧和算法，直接把我的题解搬过来。

\(\large \mathbf{Algorithm\ 1}\)

首先，先看怎样的大小为 \(\le 2\) 的割集会发挥作用。

• 首先是一条单独的树边，满足其是割边（也就是没有包含这条边的非树边）。

• 非树边+树边的组合，即包含这条树边的非树边只有当前这一条非树边。

• 树边+树边的组合，满足分别包含这两条树边的非树边的集合相同。

第三种情况不一定好理解，所以盗一张图片过来：

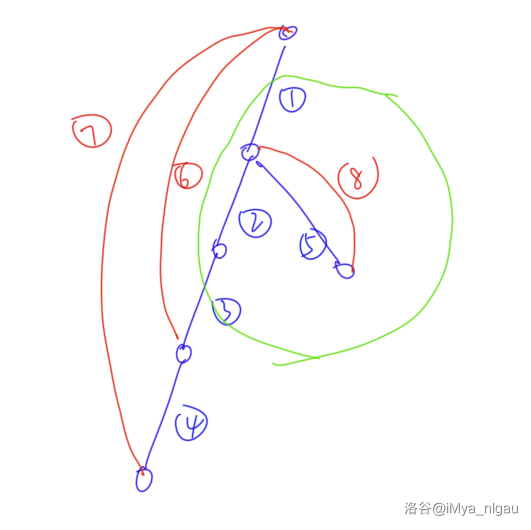
其中，蓝色是树边，红色是非树边。

然后我们发现我们需要快速计算一条树边被包含的非树边的集合，貌似不是一件很容易的时间。

这里需要用到一个 \(\text{Trick}\)。

考虑对于每条非树边随机赋一个 \([0,2^{64}-1]\) 的权值，然后定义每个点的权值表示从这个点出发的非树边的权值的异或和。

发现，若我们定义树边的权值表示一条树边被包含的非树边的权值异或和，其就是这条树边在搜索树上深度更深的端点，其子树内（包括他自己）所有的点的权值的异或和。这一步应该还是比较好理解的。

故，对于没有被非树边包含的树边，这条树边的边权显然就是 \(0\)，如果这条树边是被仅一条非树边包含，那么显然这条边的权值在非树边中也会出现。如果两条树边被包含的非树边的集合相同，等价于这两条树边的权值相同。

接下来考虑怎么求连通分量。

首先可以考虑把第一二种割集所涵盖的所有树边从搜索树上删掉（至于是哪些树边，就使用刚刚的异或哈希的技巧判断即可。），然后就会剩下若干个连通块，然后在这些连通块中分别考虑第三种割集的情况。

观察到对于所有第三种割集所对应的两条树边，我们其实只需要考虑相邻的树边，因为对于同种的配对的所有树边都在一条祖孙链上。

破防了，我要摘抄题解。

具体的，我们在 dfs 回溯的过程中维护一个 Hash 表，这样对于每条树边，我们能快速求出它下方与它配对的另一条树边，然后直接删掉两条边之间的连通块，这个连通块中一定不存在可以配对的边了，因为如果存在，也在之前的过程中删完了。这也就是说，删掉的这个连通块就是一个边三连通分量。删掉所有配对边之间部分之后，剩下的部分也是一个边三连通分量。

然后就过了。

\(\texttt{Code}\)

其他结论

\(\large \mathbf{Theory\ 4}\)

混合图 \(G\) （即可能同时包含有向边和无向边的图）可以被定向（只针对无向边）强连通，当且仅当以下两个条件满足：

• 将有向边看作无向边是，图双连通。
• 将无向边拆成一对反向的有向边后，图强连通。

先证必要性，即 \(G\) 定向之后强连通，可以推出第一个和第二个条件。

• 其实是显然的，一个强连通图的有向边变为无向边，显然图是双连通的，第二个条件同理显然。

再证必要性，即满足第一个和第二个条件的图，满足 \(G\) 可以被定向且强连通。

• 首先，如果这个图都是有向边，那显然成立。
• 考虑一种归纳的证明方法，即从 \(G\) 中取出一条无向边 \((u,v)\)，使其存在一种定向方法，形成的新图 \(G'\) 仍然满足前面两个条件，那么就可以通过归纳法证明。
• 记当前含有无向边的图为 \(G_i\)，在 \(G_i\) 中删除无向边 \((u,v)\) 得到的图是 \(G_i'\)。对于任意一个节点 \(x\)，由于原图的无向边拆对之后强连通，那么 \(G_i\) 中必然存在一条路径 \(x\sim u\)，如果这条路径没有经过 \(v\to u\)，则说明在 \(G_i'\) 中 \(x\) 可以到达 \(u\)，否则就说明在 \(G_i'\) 中 \(x\) 可以到达 \(v\)。同理，\(G_i'\) 中，要么 \(u\) 可以到 \(x\)，要么 \(v\) 可以到 \(x\)。
• 在 \(G_i'\) 中，若存在一个 \(x\)，使得 \(u\) 可以到达 \(x\)，\(x\) 可以到达 \(v\)，则 \(u\) 可以到 \(v\)，或者存在一个 \(x\)，使得 \(v\) 可以到 \(x\)，\(x\) 可以到 \(u\)，则 \(v\) 可以到 \(u\)，那么这种情况直接与连通性相反的方向对 \((u,v)\) 进行定向即可。
• 否则，只剩下 \(u,x\) 互相到达或者 \(v,x\) 互相到达的情况。意味着在 \(G_i'\) 这个图中最多只有两个强连通分量。如 \(u,v\) 互相不可达，则说明这两个强连通分量之间没有边，那就说明 \((u,v)\) 在 \(G_i\) 中国是一条割边，与第一个条件矛盾。
• 于是，我们只需要按照刚才与连通性相反的方向对 \((u,v)\) 进行定向，就可以得到 \(G_{i+1}\) 同时满足条件 \(1,2\) 且无向边的数量减少一个。
• 归纳法即可证明。

后记

结论是重要的，但是不能少了习题。