usaco 2025 Jan G
Median Heap
首先考虑解决单个询问。设 \(f_{u,0/1/2}\) 代表节点 \(u\) 的子树的中位数是 \(<,=,>m\) 的最小代价。容易 \(\mathcal{O}(n)\) 转移。
考虑对询问的 \(m\) 排序,那么过程中一些 \(2\) 会变成 \(1\),一些 \(1\) 会变成 \(0\),考虑这些变化。发现如果变的是节点 \(u\) 的值,只会对 \(fa(u),fa(fa(u)),\cdots ,1\) 有 \(f\) 的更改,因为树高 \(\log\),可以暴力修改。
最多修改 \(\mathcal{O}(n)\) 次,总复杂度 \(\mathcal{O}(n\log n)\),大常数。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5+5;
int n,Q,a[N],c[N],ty[N];
ll f[N][3];
struct node {
int x,id;
} p[N];
bool cmp(node x,node y){
return x.x<y.x;
}
int med(int x,int y,int z){
if (x>y) swap(x,y);
if (y>z) swap(y,z);
if (x>y) swap(x,y);
return y;
}
void chkm(ll &x,ll y){
if (x>y) x=y;
}
void upd(int u){
if (u*2>n){
for (int i=0; i<3; i++){
if (i==ty[u]) f[u][i]=0;
else f[u][i]=c[u];
}
return;
}
for (int i=0; i<3; i++) f[u][i]=1e18;
for (int i=0; i<3; i++){
for (int j=0; j<3; j++){
chkm(f[u][med(i,j,ty[u])],f[u*2][i]+f[u*2+1][j]);
for (int k=0; k<3; k++){
ll ad=c[u];
if (ty[u]==k) ad=0;
chkm(f[u][med(i,j,k)],f[u*2][i]+f[u*2+1][j]+ad);
}
}
}
}
void dfs(int u){
if (u>n) return;
dfs(u*2);
dfs(u*2+1);
upd(u);
}
struct quy {
int m,id;
} q[N];
bool cmq(quy u,quy v){
return u.m<v.m;
}
void Upd(int u){
int x=u;
while (x){
upd(x);
x/=2;
}
}
ll ans[N];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n;
for (int i=1; i<=n; i++){
cin>>a[i]>>c[i];
p[i]={a[i],i};
ty[i]=2;
}
sort(p+1,p+1+n,cmp);
memset(f,0x3f,sizeof f);
dfs(1);
cin>>Q;
for (int i=1; i<=Q; i++){
cin>>q[i].m;
q[i].id=i;
}
sort(q+1,q+1+Q,cmq);
int l=0,r=0;
for (int i=1; i<=Q; i++){
while (r+1<=n && p[r+1].x<=q[i].m){
ty[p[r+1].id]=1;
Upd(p[r+1].id);
r++;
}
while (l+1<=n && p[l+1].x<q[i].m){
ty[p[l+1].id]=0;
Upd(p[l+1].id);
l++;
}
ans[q[i].id]=f[1][1];
}
for (int i=1; i<=Q; i++) cout<<ans[i]<<"\n";
return 0;
}
Reachable Pairs
考虑操作的本质:
-
0:把所有相邻节点断开。 -
1:把这个点所在连通块大小减少 \(1\),连通性不变。
因为断开不能操作,考虑倒着求答案,并查集维护。复杂度 \(\mathcal{O}(n\alpha(n))\)。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5+5;
ll n,m,fa[N],sz[N],ans,res[N];
vector<int> g[N];
string s;
int ff(int x){
return x==fa[x]?x:fa[x]=ff(fa[x]);
}
ll cal(ll x){
return x*(x-1)/2;
}
void merge(int x,int y){
x=ff(x),y=ff(y);
if (x==y) return;
ans-=cal(sz[x])+cal(sz[y]);
ans+=cal(sz[x]+sz[y]);
sz[x]+=sz[y];
fa[y]=x;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>m>>s;
s=" "+s;
for (int i=1; i<=n; i++) fa[i]=i;
for (int i=1; i<=m; i++){
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
if (s[u]=='1' && s[v]=='1'){
merge(u,v);
}
}
for (int i=n; i; i--){
if (s[i]=='0'){
for (auto j : g[i]){
if (j>i || s[j]=='1'){
merge(i,j);
}
}
}
int j=ff(i);
ans+=cal(sz[j]+1)-cal(sz[j]);
sz[j]++;
res[i]=ans;
}
for (int i=1; i<=n; i++) cout<<res[i]<<"\n";
return 0;
}
Photo Op
考虑路线的样式。发现我们一定是沿着 \(x\) 轴走一点,斜着横跨,然后沿着 \(y\) 轴走一点。并且,我们横跨以及横跨结束的坐标一定是 \(X,Y,x_i,y_i\) 这些坐标。那么 \(\mathcal{O}(n^2)\) 就很简单了,枚举横跨起点和时间,可以 \(\mathcal{O}(1)\) 算出横跨终点。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 3e3+3;
int Sqrt(ll a,ll b){
ll c=a*a+b*b,y=sqrtl(c);
while (y*y<=c) y++;
while (y*y>c) y--;
return y;
}
int bst(int l,int r,int x){
return (x<l)?l:(x>r?r:x);
}
int cal(int tx,int l,int r,int x,int y){
int ty=bst(l,r,y);
return abs(x-tx)+abs(y-ty)+Sqrt(tx,ty);
}
int n,T,X,Y;
int s[N],x[N],y[N],ans[N];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>T>>X>>Y;
for (int i=1; i<=n; i++){
cin>>s[i]>>x[i]>>y[i];
}
for (int i=0; i<T; i++){
ans[i]=X+Y;
}
x[n+1]=X;
for (int i=1; i<=n+1; i++){
for (int t=0,j=1,l=0,r=2e6; t<T; t++){
while (j<=n && s[j]<=t){
if (x[j]<x[i]) l=max(l,y[j]);
if (x[j]>x[i]) r=min(r,y[j]);
j++;
}
if (l<=r) ans[t]=min(ans[t],cal(x[i],l,r,X,Y));
}
}
for (int t=0; t<T; t++) cout<<ans[t]<<"\n";
return 0;
}
忘记说明了,每一个“不能进入”的区域是由两条直线夹着的。例如进入下图黄色区域是不优的。
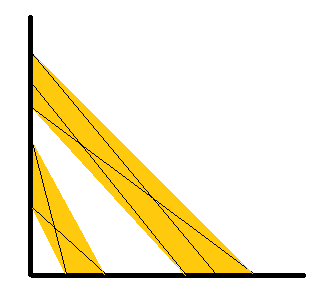
这些黄色禁止进入区域构成连通块。那么我们如果可以快速维护连通块的合并(以及对于答案的影响就可以了)。具体的:
-
每一个连通块可以用 \(min_x,max_x,min_y,max_y\) 表示。
-
答案和连通块可以用 multiset 维护。
-
相交的判断:不是 \(max_{xa}\le min_{xb}\) 并且 \(max_{ya}\le min_{yb}\)
即可(\(a\) 在 \(b\) 左边)。 -
对于一个横跨起点的结束点最佳:如果我们可以直接到达 \([y_{mn},y_{mx}]\) 之间的点,那么 \(Y<y_{mn}\) 则 \(y_{mn}\) 最优,\(Y>y_{mx}\) 则 \(y_{mx}\) 最优,否则 \(Y\) 就可以直接到,\(Y\) 最优。其实和暴力一样。
-
两个连通块的并合并 \(min_x,max_x,min_y,max_y\) 就可以了。
-
初始加入 \((0,0),(\infty,\infty)\) 两条线可以避免边界判断。
时间复杂度 \(\mathcal{O}(n\log n)\)。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 3e5+5;
int Sqrt(ll a,ll b){
ll c=a*a+b*b,y=sqrtl(c);
while (y*y<=c) y++;
while (y*y>c) y--;
return y;
}
int n,T,X,Y;
vector<pair<int,int> > g[N];
multiset<ll> sns;
#define F first
#define S second
#define pi pair<int,int>
#define ppi pair<pi,pi>
set<ppi> cn;
bool ist(ppi a,ppi b){
if (a.F.S<=b.F.F && a.S.S<=b.S.F) return 0;
return 1;
}
int bst(int l,int r,int x){
return (x<l)?l:(x>r?r:x);
}
void Add(ppi l,ppi r,int f){
pi xr={l.F.S,r.F.F};
pi yr={l.S.S,r.S.F};
ll cx=bst(xr.F,xr.S,X),cy=bst(yr.F,yr.S,Y);
ll ans=abs(X-cx)+abs(Y-cy)+Sqrt(cx,cy);
if (f==1) sns.insert(ans);
else sns.erase(sns.find(ans));
}
void add(ppi x,int f){
auto it=cn.lower_bound(x);
if (it!=cn.begin()){
Add(*prev(it),*it,f);
}
if (next(it)!=cn.end()){
Add(*it,*next(it),f);
}
if (it!=cn.begin() && next(it)!=cn.end()){
Add(*prev(it),*next(it),-f);
}
}
void uni(ppi &a,ppi b){
a.F.F=min(a.F.F,b.F.F);
a.F.S=max(a.F.S,b.F.S);
a.S.F=min(a.S.F,b.S.F);
a.S.S=max(a.S.S,b.S.S);
}
void ins(int x,int y){
ppi p={{x,x},{y,y}};
while (1){
auto it=cn.lower_bound(p);
if (it!=cn.end() && ist(p,*it)){
add(*it,-1),uni(p,*it);
cn.erase(it);
continue;
}
if (it!=cn.begin() && ist(*prev(it),p)){
auto _it=prev(it);
add(*_it,-1),uni(p,*_it);
cn.erase(_it);
continue;
}
break;
}
cn.insert(p);
auto it=cn.lower_bound(p);
add(*it,1);
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>T>>X>>Y;
ins(0,0);
ins(1e9,1e9);
for (int i=1; i<=n; i++){
int s,x,y;
cin>>s>>x>>y;
g[s].push_back({x,y});
}
for (int i=0; i<T; i++){
for (auto u : g[i]){
ins(u.first,u.second);
}
cout<<(*sns.begin())<<"\n";
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号