CF 191 D
一条边最多在一个简单环当中，我们发现有几种情况：
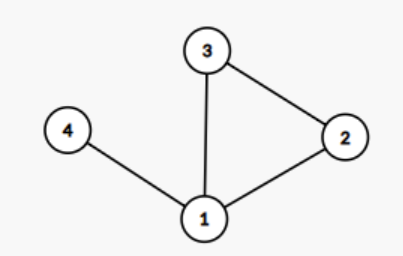
这个显然直接选一个环覆盖再加上一条 \(1\leftrightarrow 4\) 的边。如果 \(4\) 没有，那么也是直接选一个环覆盖。
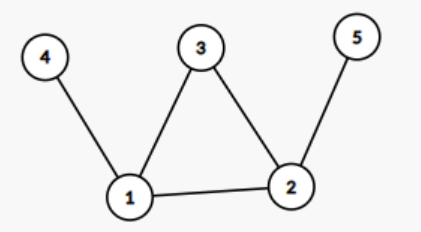
如果是有两个及以上的”突出“的边，那么我们显然不用选环，而是把换拆成一些链，这样更优。这个图中就是拆成 \(4\leftrightarrow 1\leftrightarrow 3\leftrightarrow 2\) 和 \(1\leftrightarrow 2\leftrightarrow 5\)。
那么我们发现，所有可以直接覆盖的环都是”突出“的边小于等于 \(1\) 个的。剩下的选的都是链。
求链的个数，其实就是链的端点个数除以 \(2\)。显然当 \(deg_u\) 是偶数的时候，就相当于有若干条链进入它，再从它出去，一定不是一个链的端点；反之如果是奇数，一定会是。
容易发现我们计算 \(deg_u\) 是奇数的个数的时候可以不考虑环（因为没有”突出“的边的环的所有 \(deg\) 都为 \(2\)）。
求环的话，用 tarjan 边双可以做到 \(\mathcal{O}(n)\)。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 5e5+5;
struct edge {
int nxt,to;
} ed[N<<1];
int lnk[N],tot=1,deg[N],vis[N];
int n,m,tim,dfn[N],low[N],drg[N],brd[N<<1],vid[N],cc;
vector<int> cir[N];
void ade(int u,int v){
ed[++tot]={lnk[u],v};
lnk[u]=tot,deg[u]++;
}
void tarjan(int u,int fa){
dfn[u]=low[u]=++tim;
for (int i=lnk[u],v; v=ed[i].to,i; i=ed[i].nxt){
if (!dfn[v]){
tarjan(v,u);
low[u]=min(low[u],low[v]);
if (low[v]>dfn[u]){
brd[i]=brd[i^1]=1;
}
}
else if (v^fa){
low[u]=min(low[u],dfn[v]);
}
}
}
void dfs(int u){
vis[u]=1;
cir[cc].push_back(u);
for (int i=lnk[u],v; v=ed[i].to,i; i=ed[i].nxt){
if (!brd[i] && !vis[v]){
dfs(v);
}
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>m;
for (int i=1; i<=m; i++){
int u,v;
cin>>u>>v;
ade(u,v);
ade(v,u);
}
if (!m){
cout<<0<<" "<<0<<"\n";
return 0;
}
for (int i=1; i<=n; i++){
tarjan(i,0);
}
for (int i=1; i<=n; i++){
if (!vis[i]){
cc++;
dfs(i);
}
}
if (cc==1){
cout<<1<<" "<<m<<"\n";
return 0;
}
int ans=0;
for (int i=1; i<=n; i++){
if (deg[i]&1){
ans++;
}
}
ans/=2;
for (int i=1; i<=cc; i++){
if (cir[i].size()!=1){
int cnt=0;
for (auto u : cir[i]){
if (deg[u]>2){
cnt++;
}
}
if (cnt<=1){
ans++;
}
}
}
cout<<ans<<" "<<m<<"\n";
return 0;
}
但是我翻了一下最短代码，好像有很短的。现在来研究怎么把代码写简单。先贴代码。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5+5;
int n,m;
vector<int> g[N];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>m;
for (int i=1; i<=m; i++){
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
int ans=0;
for (int i=1; i<=n; i++){
if (g[i].size()&1){
ans++;
}
}
for (int i=1; i<=n; i++){
if (g[i].size()==2){
int x=g[i][0],y=g[i][1];
if (x==y){
g[x].clear();
ans+=2;
}
else{
g[x][g[x][0]!=i]=y;
g[y][g[y][0]!=i]=x;
}
}
}
cout<<ans/2<<" "<<m<<"\n";
return 0;
}
首先，因为找 \(deg_u\) 奇数个数不会有任何影响，所以我们先求这一个。下面的操作相当于求环。
我们知道，满足条件的环一定是最多有一个”突出“的边的，因此优两种情况：\(0\) 个和 \(1\) 个。分别考虑：
- 如果是 \(0\) 个，下面的操作显然可行。其实这个连通块就是一个环，我们每一次选一个点把点两边的连起来再把这个点删掉。
- 如果是 \(1\) 个，那么我们在没有”突出“的边的部分可以像上面进行一样的操作。其实可以不管那个有”突出“的边的部分，最后还是会压缩成 \(1 \leftrightarrow 2\)，\(1\leftrightarrow 2\)，\(2\leftrightarrow 3\) 的形式。遇到那个有”突出“的边的部分循环会跳过。
因此，这就有了一个及其好写的 \(\mathcal{O}(n)\) 做法。
