PageRank算法

PageRank算法

算法中心思想

（1）数量假设：在网页模型图中，一个网页接收到的其他网页指向的入链（in-links）越多，说明该网页越重要。

（2）质量假设：当一个质量高的网页指向（out-links）一个网页，说明这个被指向的网页质量也高。

可以这样类比：在一次投票过程中，得票数多的人，其声望排名肯定相对较高；此外，被声望较高的人投票的人，说明其声望排名也较高。

算法和公式

\[PR(a)_{i+1} = \sum_{i=0}^n \frac {PR(Ti)_i}{L(Ti)} \]

\(PR(Ti)\)代表的是其他节点(指向节点a的节点)的PR值；

\(L(Ti)\)代表的是其他节点(指向节点a的节点)的出链数；

\(i\)代表循环次数。当\(i=0\)时，所有节点的初始值初始化为\(\frac 1 N\)（N为所有节点数目，及网页数目）。

PR值需要通过多次循环迭代才能达到一个稳定值。

【示例】

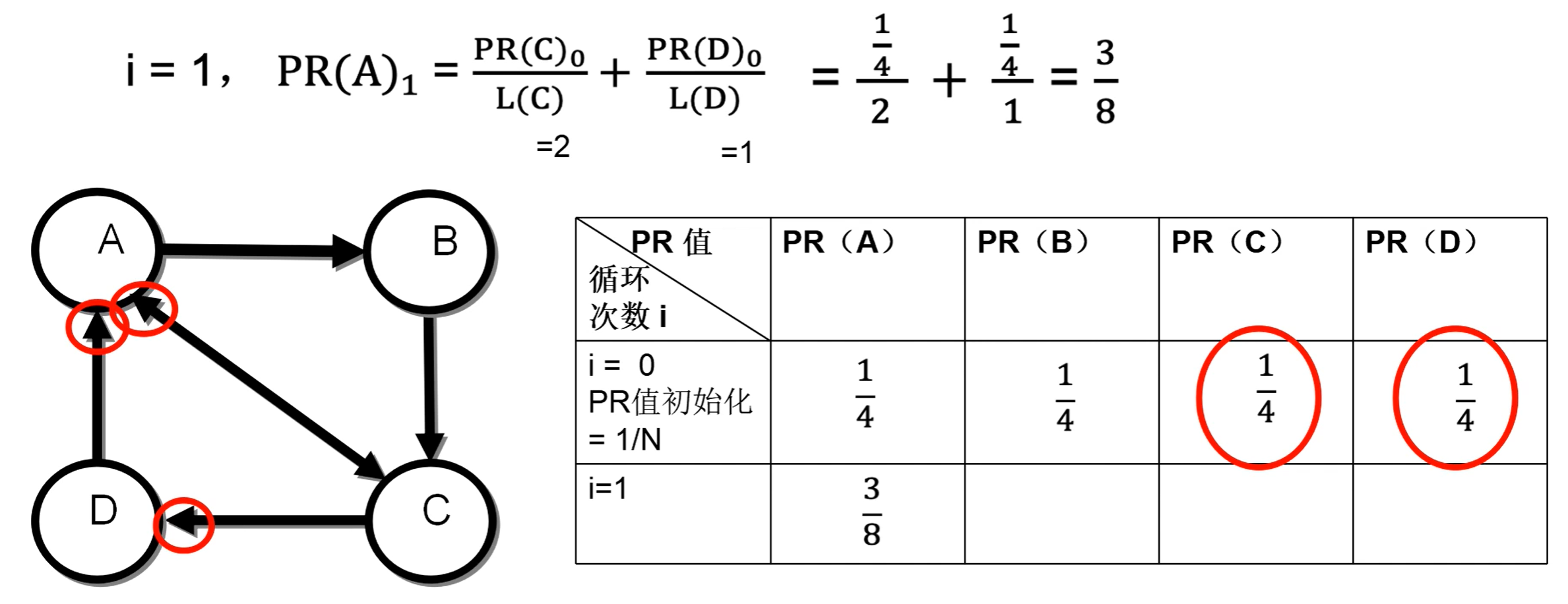
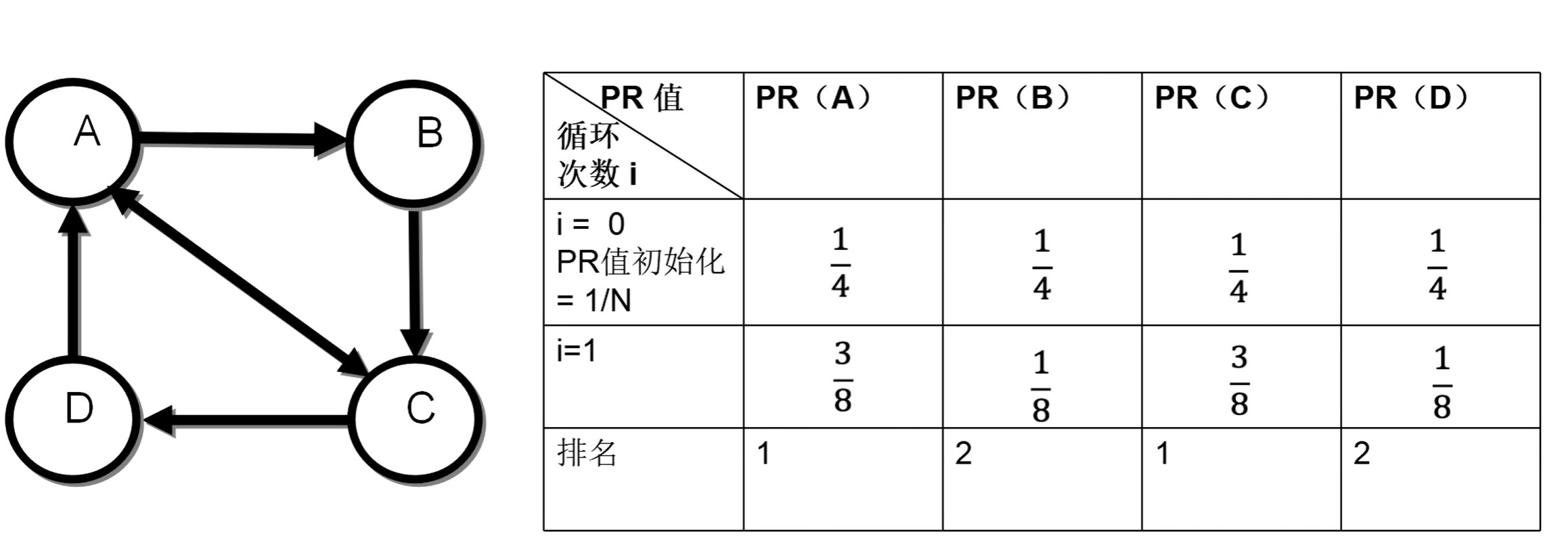
可见，节点A的PR值与其在上一次循环中的PR值没有任何关系。

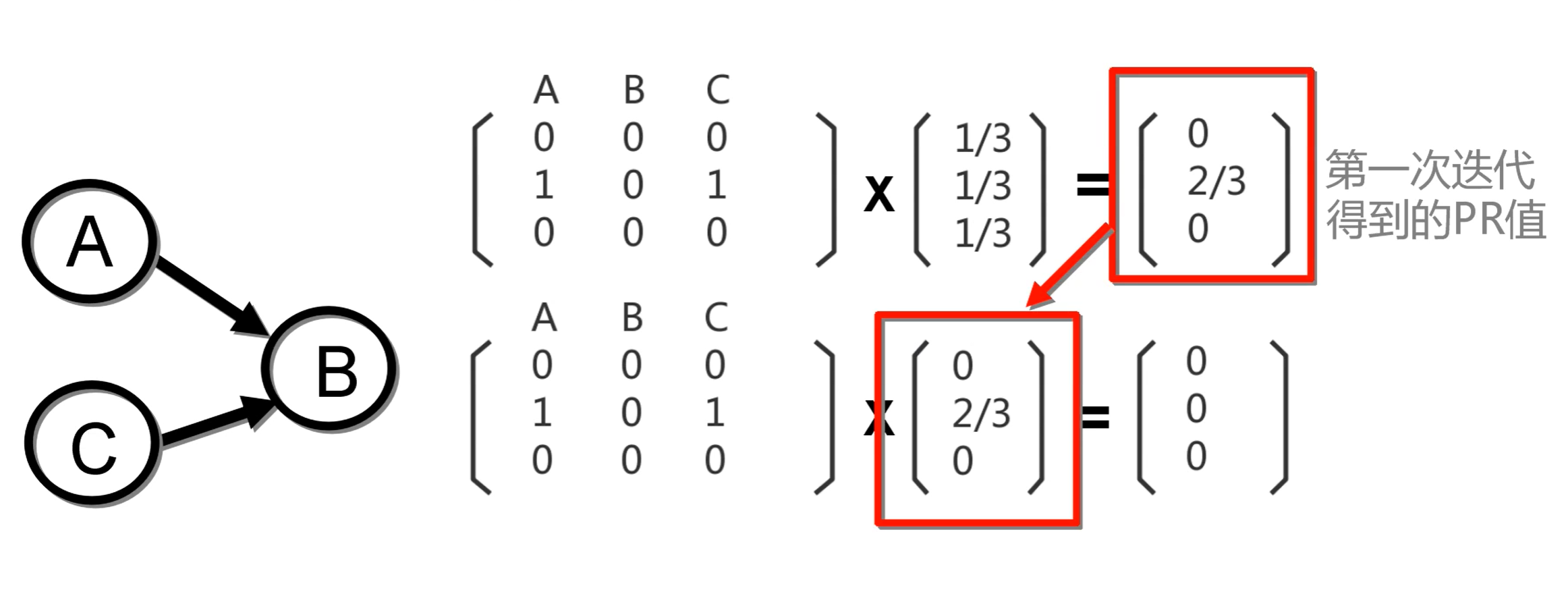
【矩阵化表达】

通过矩阵化表达，快速求解PR值：

\[PR(a) = M*V \]

矩阵M为图的马尔科夫矩阵，V为上一次循环各节点PR值构成的矩阵。

Dead Ends问题

如上图所示，B没有任何出链，则造成Dead Ends问题。经过多次循环之后，其会导致网站的权重变为0。

【解决方案】Teleport——将节点图转化成列转移概率矩阵，再修正马尔科夫矩阵M

\[\bold {修正过程}： M \leftarrow M + a^T(\frac {ee^T} n) \]

\(\bold a=[\bold a_0,\bold a_1,...,\bold a_n]\)（\(\bold a_i\)为行向量），当修正前的M中第\(i\)列数值全为0（即对应节点无出链）时，则\(\bold a_i\)中的元素全为1，否则矩阵\(\bold a_i\)中元素全为0。\(ee^T\)为由元素1填满的n*n矩阵，\(n\)为M矩阵的行数（或列数）。

【示例】

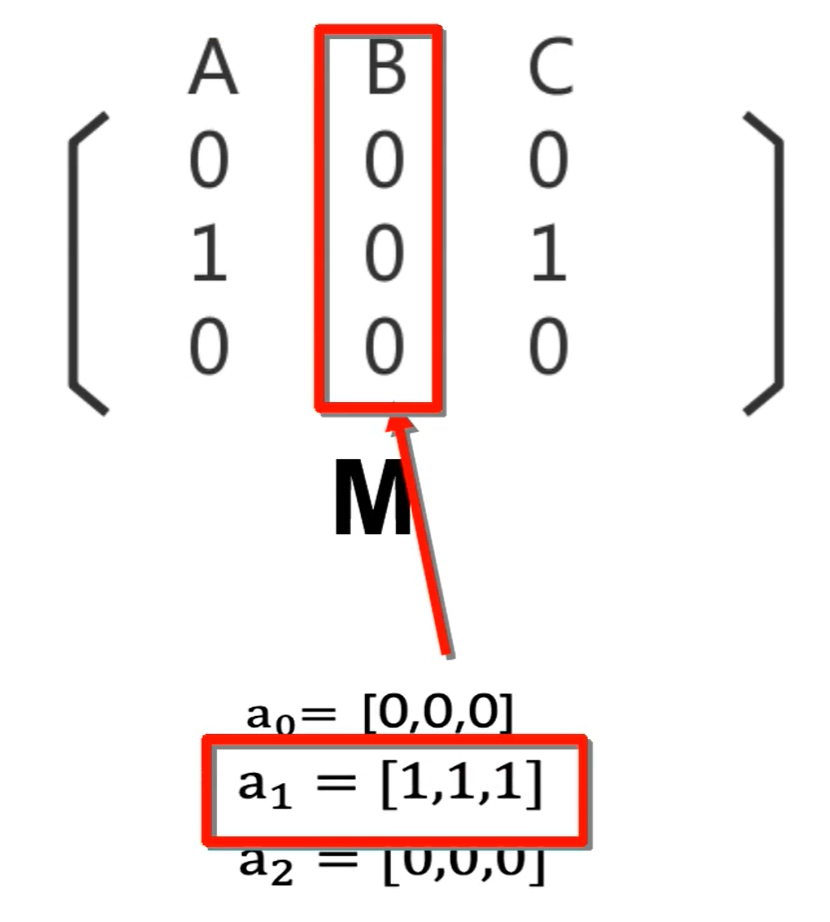
如上图，因为第1列元素全为0，所以有\(\bold a_1 =[1,1,1]\)，而第0列和第2列不全为0，所以\(\bold a_0,\bold a_2\)元素全为0。

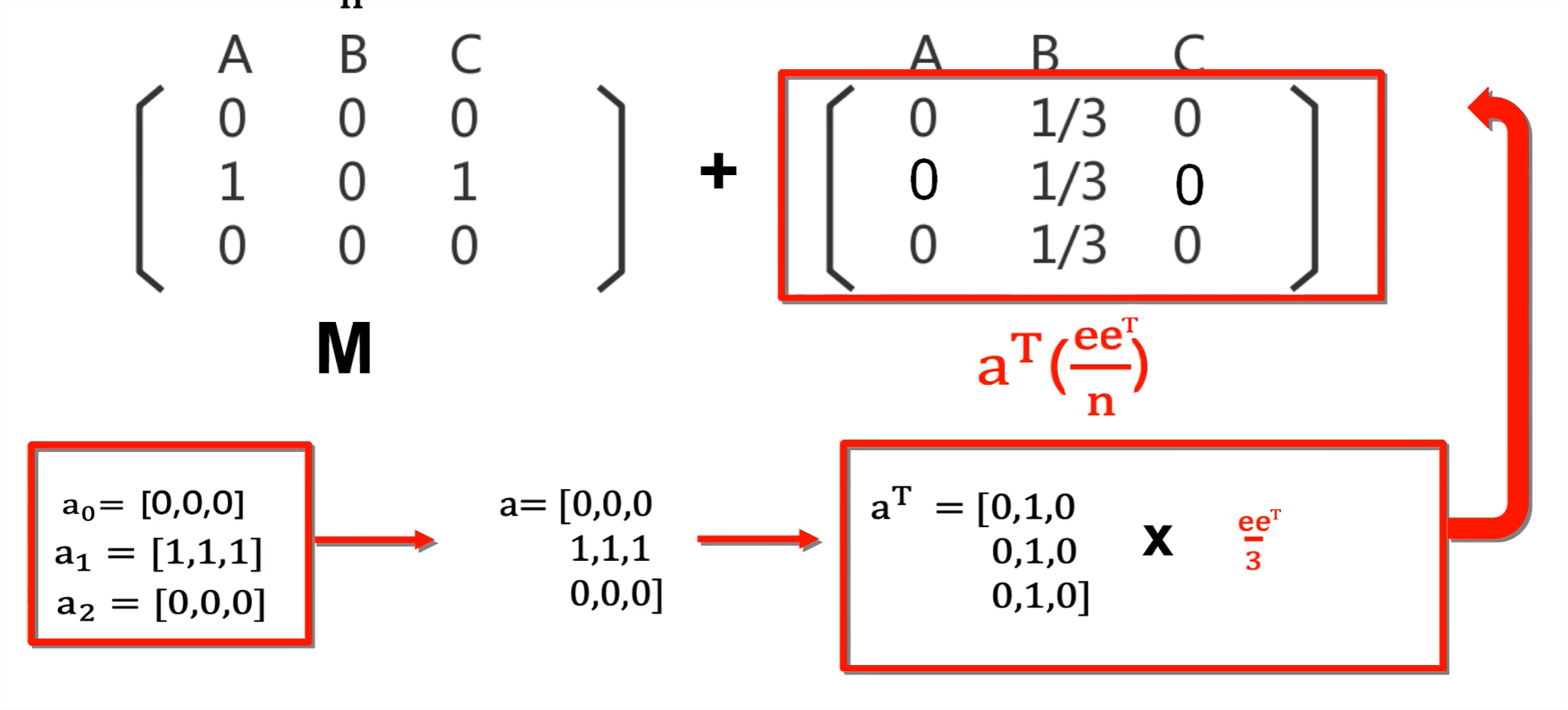
对M矩阵进行修正的过程如上图所示。

Spider Traps问题

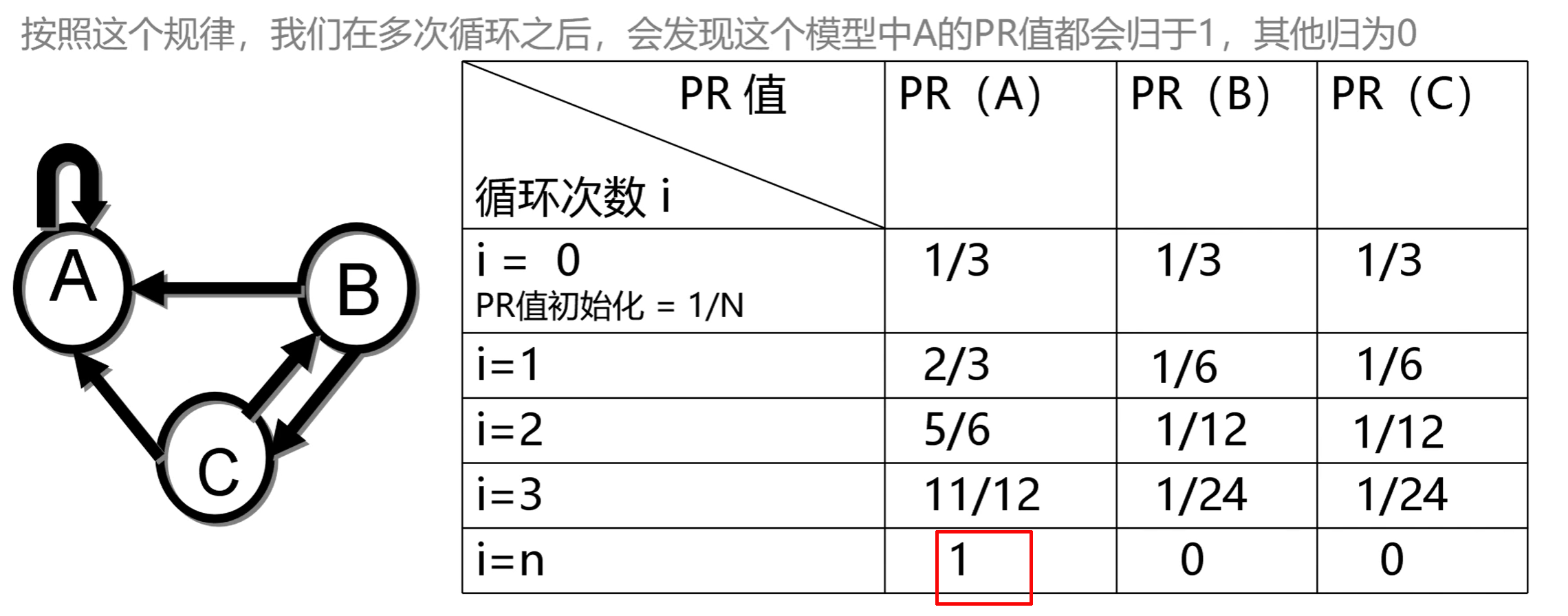
A节点与其他节点之间不存在出链（更具体地说，节点A存在自环），此为Spider Traps问题。由表格可见，其会导致网站权重变为向某一个含自环的节点偏移（因为此节点PR值最终会趋于1）。

【解决方案】Random Teleport——将节点图转化成列转移概率矩阵，再修正马尔科夫矩M（随机浏览模型）

\[{修正过程}： M \leftarrow \beta M + (1-\beta )\frac {ee^T} n \]

\(\beta\)为跟随出链打开网页的概率；\(1-\beta\)为随机跳转到其他网页的概率，例如浏览网页A时有一定概率会打开网页B或C。

\(ee^T\)为由元素1填满的n*n矩阵，\(n\)为M矩阵的行数（或列数）。

【示例】

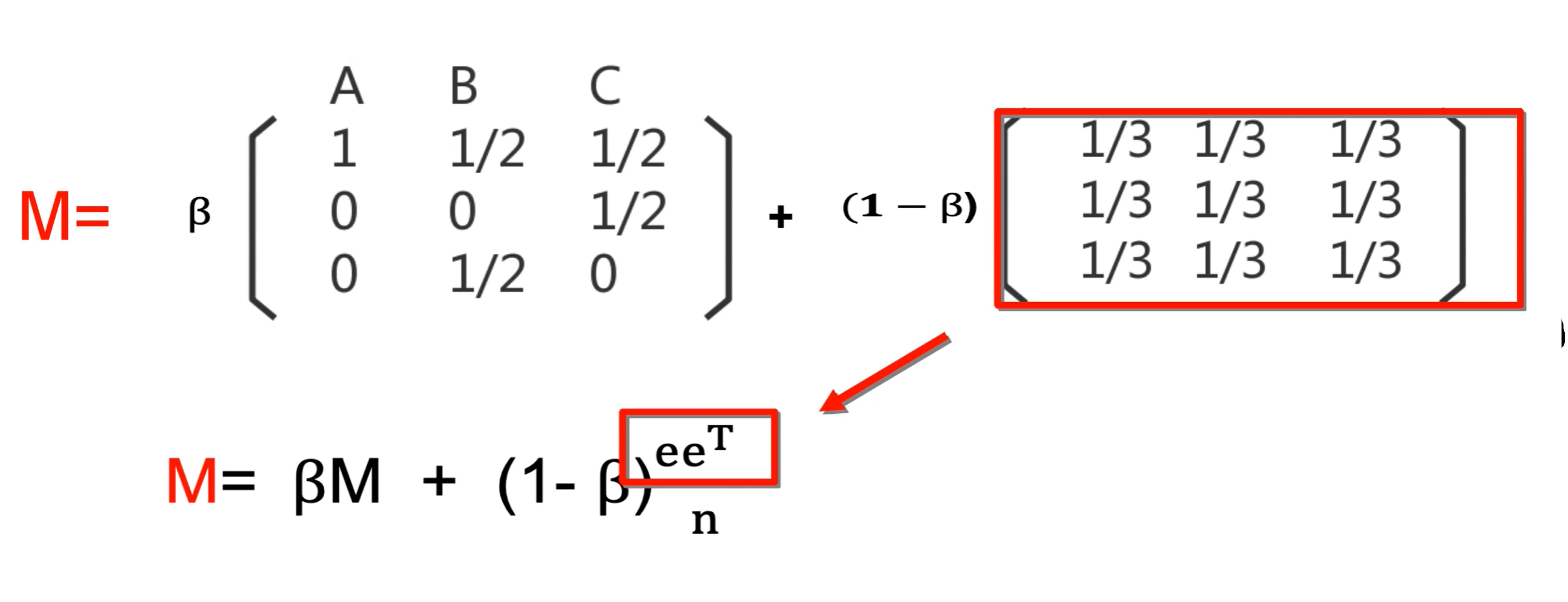
\(\beta\)值取值范围一般是在[0.8 , 0.9]。

如上图所示，修正后的M矩阵中，A所在的列中元素值已然发生了改变。




【思考】在使用\(\beta\)解决Spider Traps问题时能否顺便解决Dead Ends问题？

​ 答：不能，使用\(\beta\)解决Dead Ends问题时，修正后的M不满足转移概率矩阵的性质：列之和为1。因此，禁用\(\beta\)是不足以解决Dead Ends问题的。

最终修正公式

当同时遇到Dead Ends问题和Spider Traps问题时，修正公式如下：

\[PR(a) = \bigg [\beta \bigg ( M + a^T(\frac {ee^T} n) \bigg) +(1-\beta )\frac {ee^T} n \bigg]*V \]

PageRank的优缺点

优点

（1）通过网页之间的链接来决定网页的重要性，一定程度消除了对认为排名结果的影响；

（2）离线计算PageRank值，提升了查询效率。

缺点

（1）存在时间长的网站，PageRank值会越来越大（因为其入链会越来越多）；新生的网站，PageRank值增长慢（因为其初始入链相对较少且增长慢）；

（2）非查询相关的特性，查询结果会偏离搜索内容；

（3）可以通过“僵尸网站”或链接，认为刷PageRank值；

【参考文献】这系列视频PageRank算法讲得很棒，本文主要是对这个视频学习后的总结。