洛谷 P2767 树的数量

题目传送门

题目大意

求满足有 n 个相同节点，至多 m 叉的树的数量，答案对 10007 取模。
保证 n，m \(\leqslant\) 127。

思路

emmm... 很容易想到的就是 dp，设 dp[i][j] 表示包含 i 个节点，根节点至多 j 叉的树的数量。首先很显然有 dp[0][0-127] = 1，也就是没有节点时有一种空树方案；接着 dp[1][0] = 1，即一颗只有根节点的树。

边界条件处理完了之后就要求 dp[i][j]。
先放个图：

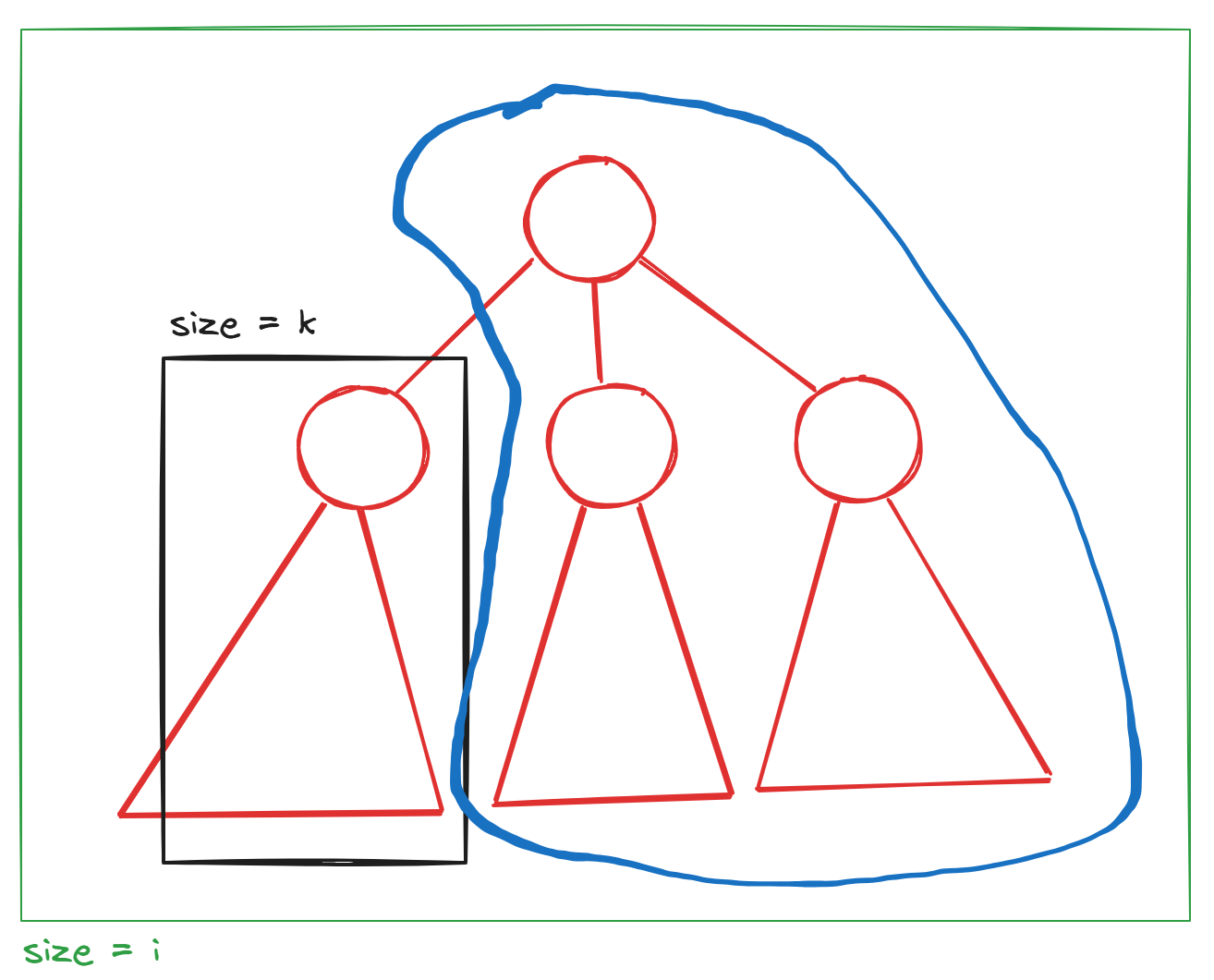
假设现在这里有一颗共 i 个节点，根节点至多 j 叉的树，图中三角表示一个子树（可以为空）。图上只有 3 个叉只是一个栗子，而且可以有空子树。那么枚举其中一个子树（黑色框选部分）大小为 k，那么把这颗子树拿开就会剩下一个 i-k 个节点，根节点至多j-1 叉的树（蓝色部分）。现在来计算这个被拿走的子树，就是一颗总共 k 个节点，根节点至多 m 叉的树。于是这两个部分分别对应 dp[i-k][j-1] 和 dp[k][m]，两项相乘再将所有枚举的 k 计算出的结果相加即可得 dp[i][j]。

感觉够不上紫。

Code

#include<bits/stdc++.h>
using namespace std;
int dp[130][130],mod=10007;
int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=0;i<=127;i++) dp[0][i]=1;
	dp[1][0]=1;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			for(int k=0;k<i;k++) dp[i][j]=(dp[i][j]+dp[k][m]*dp[i-k][j-1]%mod)%mod;
	printf("%d\n",dp[n][m]);
	return 0;
}

短短 14 行，和上面思路完全一样。

\(\sim\) ❀完结撒花❀ \(\sim\)