题目描述
给定一棵由 \(n\) 个节点构成的树,可以使用两种颜色(假定为红和蓝)进行染色,并且每个节点可以选择染红色、蓝色或者不染色。设红色的节点有 \(r\) 个,蓝色的节点有 \(b\) 个,要求染色后的节点同时满足以下三个条件:
\(r + b\) 最大化;
\(r,b \neq 0\);
任意两个相邻的节点不能被染成相同的颜色。
询问满足要求的染色方案数及 \(r\),\(b\) 的所有可能值。
思路
一道 DP 好题!
不难发现两种颜色总和最大一定是 \(n-1\),及最多只能有一个节点不被染色。又注意到条件三:任意两个相邻的节点颜色不相同,可以得出结论一定有且仅有一个节点不被染色(这个结论并不难想,看不明白的建议画图推导一下)。
于是我们想到可以枚举不染色的节点,进行 DP 来推导总共有 \(k\) 个节点染成红色的方案可行性。
如何计算?放两张图。
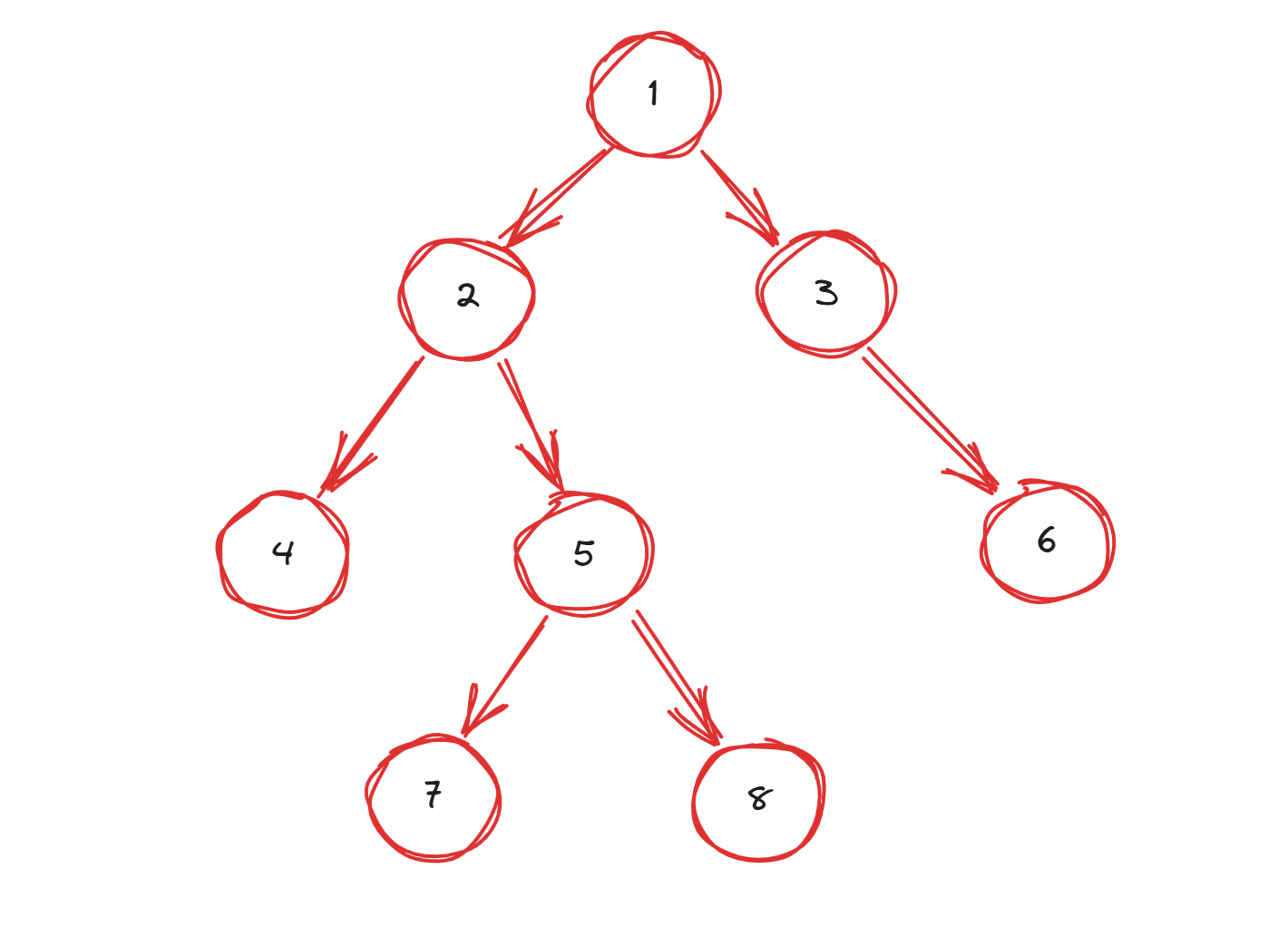
假设这是初始的树,现在我们枚举到节点 \(5\) 是没有颜色的节点。
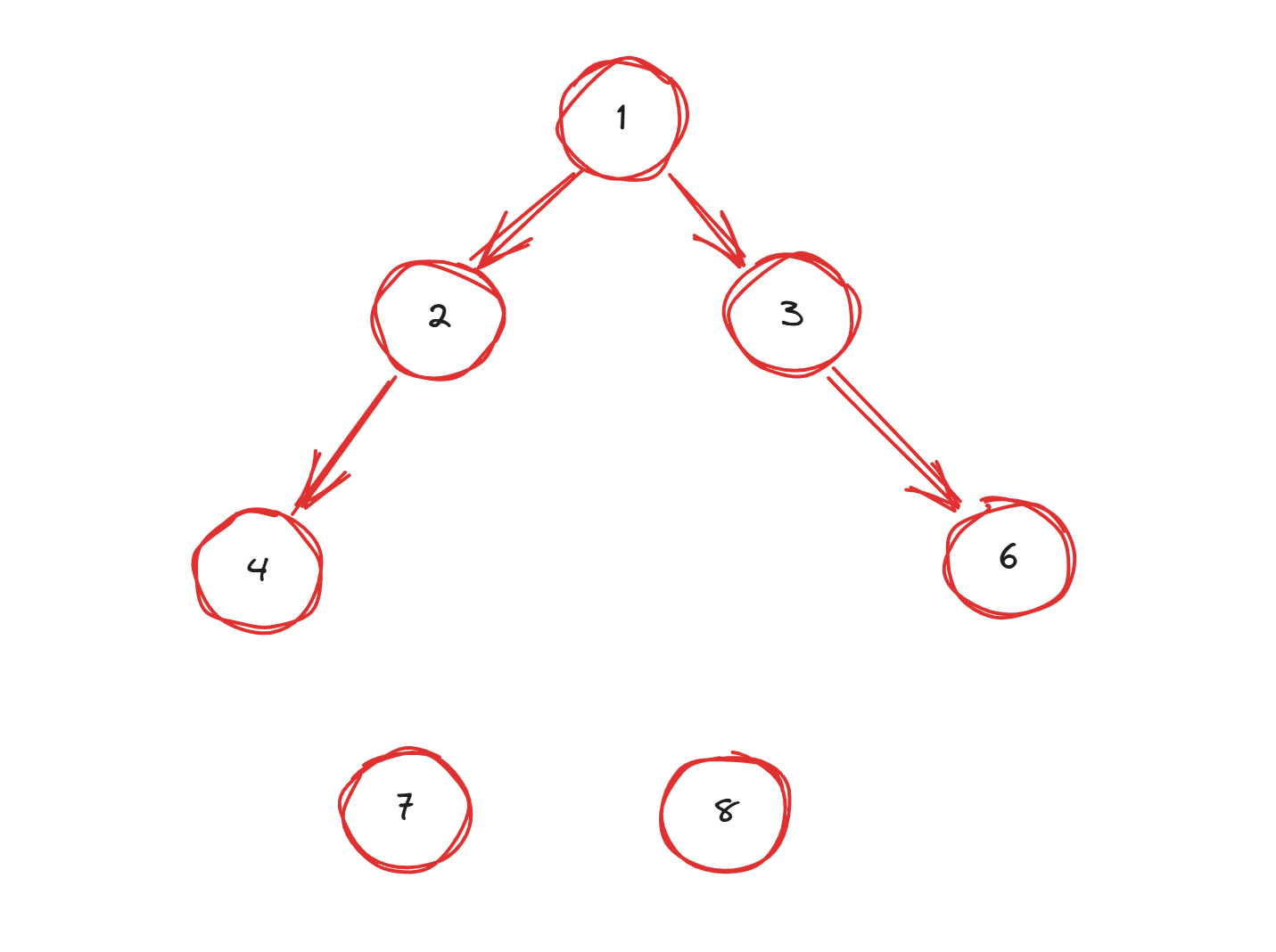
可以看出删除一个节点后原树会被分成几个小连通块,所以我们只需要根据原树的子树大小计算出每个小块的大小,类似于 01 背包处理即可。
于是现在这个思路很完整了。
实现
在思路完整之后,代码的实现其实并不难。只需要注意几个小小的细节:dfs 求取子树大小 siz[i],输出答案时需要枚举 $i \in \left [ 1 \sim n-2 \right ] $。
Code
#include<bits/stdc++.h>
using namespace std;
vector<int> G[5005];
int siz[5005],dp[5005],c[5005],ans[5005],n;
void dfs(int u,int father){
siz[u]=1;
for(auto v:G[u]){
if(v==father) continue;
dfs(v,u);
siz[u]+=siz[v];
}
} //计算子树大小。
void find_ans(int u,int father){
int tot=0;
for(auto v:G[u]){
if(v==father) continue;
c[++tot]=siz[v]; //将不染色节点的儿子子树大小加入类似于重量的 c 数组。
}
c[++tot]=n-siz[u]; //由于删除一个节点后,不包含在该节点子树中的连通块至多只有一个,所以只需用原树大小减去该节点子树大小。
memset(dp,0,sizeof(dp));
dp[0]=1; //初始化。
for(int i=1;i<=tot;i++)
for(int j=n;j>=c[i];j--)
if(dp[j-c[i]]==1) dp[j]=1; //如果 j-c[i] 的方案可行,那么 j 也可行。
for(int i=1;i<=n;i++) ans[i]=max(ans[i],dp[i]);
for(auto v:G[u]){
if(v==father) continue;
find_ans(v,u); //继续 dfs。
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<n;i++){
int u,v;
scanf("%d%d",&u,&v);
G[u].push_back(v),G[v].push_back(u);
}
dfs(1,0);
find_ans(1,0);
int cnt=0;
for(int i=1;i<n-1;i++) //i < n-1 是因为至少有一个蓝点和一个不染色节点。
if(ans[i]==1) cnt++; //求方案数。
printf("%d\n",cnt);
for(int i=1;i<n-1;i++)
if(ans[i]==1) printf("%d %d\n",i,n-i-1);
return 0;
}
\(\sim\) ❀完结撒花❀ \(\sim\)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号