20250812 - 全源最短路 总结

一.多源单汇最短路

概念

多个点跑最短路到某一个特定的点。

方法一：

跑 \(n\) 遍 Dijkstra 或 bellman-ford（SPFA）算法，时间复杂度： \(O(nmlog_2m)\)，当 \(n\) 到了 \(10^5\) 不就寄了吗？

方法二：

反向建图，这样就是一个经典的单源最短路径。

二.Floyd算法

Floyd其实更像是一个暴力动态规划，但他能求出每一对点的最短路，并且常数也很小，只有三个 \(for\) 循环，没有其他奇奇妙妙的东西，相比于跑 \(n\) 遍 Dijkstra，它在稠密图表现得很优秀，因为稠密图 \(m \approx n^2\)。

他的思想很简单：枚举中转点，看直接到达和经过中转点哪个更短。最终，每一对的最短路就出来了

for(int k = 1;k <= n;k++)
  for(int i = 1;i <= n;i++)
    for(int j = 1;j <= m;j++)
      dp[i][j] = min(dp[i][j],dp[i][k]+dp[k][j]);

所以：发明 Floyd 的人真是个天才

三.Johnson 全源最短路径算法

传说 Floyd 的时间复杂度为 \(O(n^3)\)，要是 n 再大一点就寄了。我们很容易想到跑 \(n\) 遍 Dijkstra，这样子就求出了每对点的最短路。

但是 Dijkstra 不能处理负权图，用 spfa 的时间复杂度还不如 Floyd，怎么办呢，我们很容易想到把每个点都加上一个数，到时候最短路就减去 \(kx\)，但这样子是错误的，请看 VCR：

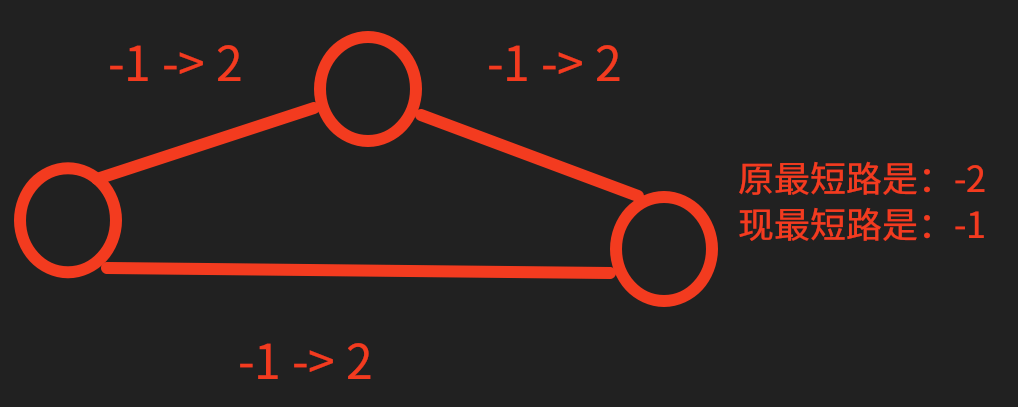
我们新建一个虚拟节点（在这里我们就设它的编号为 \(0\) ）。从这个点向其他所有点连一条边权为 \(0\) 的边。

用 bellman（SPFA） 计算从 \(S\) 出发的单源最短路，到 \(i\) 的最短路记作 \(h_i\)，即为点 \(i\) 的势能。

对于原图上的边 \((u, v, w)\)，把它看成 \((u, v, w + h_u - h_v)\)，然后正常做 Dijkstra 即可这样的边权标注方法可以使得每条边权非负，并且能够得到原图最短路。

注意：写的时候一定要小心，不然调试可是很爽的！！！！

---

01bfs

把边权为 \(0\) 的边权放在队首，否则放在队尾。

例题

1. 灾后重建

这道题可以把已经建好的当做中转点跑 Floyd 就好了！！！

#include <bits/stdc++.h>

using namespace std;
#define ll long long
const int MAXH = 505;
const int INF = 1e9;
int n,m,q;
int t[MAXH];
int f[MAXH][MAXH];
void data(int k){
	for(int i = 1;i <= n;i++)
		for(int j = 1;j <= n;j++)
			f[i][j] = min(f[i][k]+f[k][j],f[i][j]);
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n + 10;i++)
		for(int j = 1;j <= n + 10;j++)
			f[i][j] = INF;
	for(int i = 1;i <= n;i++)
		scanf("%d",&t[i]),f[i][i] = 0;
	
	for(int i = 1;i <= m;i++){
		int x,y,w;
		scanf("%d%d%d",&x,&y,&w);
		x++,y++;
		f[x][y] = f[y][x] = min(w,f[x][y]);
	}
	scanf("%d",&q);
	int cur = 1;
	while(q--){
		int x,y,w;
		scanf("%d%d%d",&x,&y,&w);
		x++,y++;
    
		while(t[cur] <= w && cur <= n){
      data(cur++);
    }
    if(t[x] > w || t[y] > w) {
      printf("-1\n");
    }
    else if(f[x][y] != INF)
      printf("%d\n",f[x][y]);
    else{
      printf("-1\n");
    } 
	}
	return 0;
}

---

总结：Floyd 适合在稠密图或数据范围比较小的情况下跑，Johnson 适合在稀疏图或相对较大时跑！