[CSP-S模拟测试51]题解

错失人生中第一次AK的机会……

 

A.attack

支配树板子题。考场上发明成功√

首先支配树上两点路径之间的点都是必经之点，根据这个性质我们就可以yy出建树的方法。跑拓扑，在每个点(设为$x$)即将入队之前利用反图找到$x$的入点，显然这些点都不是根到$x$的必经之点。那么谁才是呢？这些点在支配树上的lca。因为建树是拓扑进行的，所以$x$入队一定是在它的入点入队之后，也就是说这些点此时已经在树上了，那么就可以查询到这些点在支配树上的lca并由它向$x$连边(支配树上)。

如果把根节点深度设为1，那一个点到根节点路径上必经之点的个数就是它的深度。对于每次询问，找到左右询问点的lca即可。

//你让我考场发明支配树？？？
//当时学圆方树的时候看过一眼 瞎打吧...
//跑拓扑 反图+lca乱搞建出树 有环应该无所谓？
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int N=1e5+5;
int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
	return x*f;
}
int n,m,Q;
int to[N],head[N],nxt[N],tot,deg[N],fa[N][22],dep[N];
int qr[N];
vector<int> rev[N],g[N];
queue<int> q;
void add(int x,int y)
{
	to[++tot]=y;
	nxt[tot]=head[x];
	head[x]=tot;
	deg[y]++;
	rev[y].push_back(x);//反图
}
void link(int x,int y)
{
	g[x].push_back(y);
	fa[y][0]=x;
	for(int i=1;i<=20;i++)
		fa[y][i]=fa[fa[y][i-1]][i-1];//不知道这样行不行...
}
int lca(int x,int y)
{
	if(dep[x]>dep[y])swap(x,y);
	for(int i=20;i>=0;i--)
		if(dep[fa[y][i]]>=dep[x])y=fa[y][i];
	if(x==y)return x;
	for(int i=20;i>=0;i--)
		if(fa[y][i]!=fa[x][i])x=fa[x][i],y=fa[y][i];
	return fa[x][0];
}
int main()
{
/*freopen("dt.in","r",stdin);
freopen("my.out","w",stdout);*/
	n=read();m=read();Q=read();
	for(int i=1;i<=m;i++)
	{
		int x=read(),y=read();
		add(x,y);
	}
	q.push(1);dep[1]=1;
	while(!q.empty())
	{
		int x=q.front();q.pop();
		for(int i=head[x];i;i=nxt[i])
		{
			int y=to[i];
			deg[y]--;
			if(!deg[y])
			{
				int anc=0,sz=rev[y].size();
				for(int j=0;j<sz;j++)
				{
					int z=rev[y][j];
					if(anc)anc=lca(anc,z);//所有入点的lca在支配树上才是x的父亲
					else anc=z;
				}
				link(anc,y);dep[y]=dep[anc]+1;
				q.push(y);
			}
		}
	}
	while(Q--)
	{
		int k=read();
		for(int i=1;i<=k;i++)
			qr[i]=read();
		if(k==1)
		{
			printf("%d\n",dep[qr[1]]);
			continue;
		}
		int now=lca(qr[1],qr[2]);
		for(int i=3;i<=k;i++)
			now=lca(now,qr[i]);
		printf("%d\n",dep[now]);//深度即到根节点必经之点的个数
	}
	return 0;
}

 题面没说清给的是DAG，然而我试了一组手玩的带环样例觉得有环没事就按DAG打了……这是不对的，DAG建支配树比普通有向图建支配树简单多了。如果想学一般有向图的建树方法请移步这里。

B.reverse

把操作逆向进行，先把a和b变成等长，然后一起逆向推回去即可。

考试千万别用$STL\ string$QAQ！超慢！！另外$cin.tie(0)$不能乱用啊！就因为这点破事没AK555

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int T,cnt1,cnt2;
struct str
{
    char s[2005];
    int size;
    void up()
    {
        size=strlen(s+1);
    }
};
bool eq(str s1,str s2)
{
    if(s1.size!=s2.size)return 0;
    for(int i=1;i<=s1.size;i++)
        if(s1.s[i]!=s2.s[i])return 0;
    return 1;
}
void show(str s)
{
    for(int i=1;i<=s.size;i++)
        printf("%c",s.s[i]);
    putchar('\n');
}
void work()
{
    str a,b;
    scanf("%s",a.s+1);scanf("%s",b.s+1);
    a.up();b.up();
    str ta=a,tb=b;
    int tn=a.size,tm=b.size;
    if(tn>tm)
    {
        for( ;tn>tm;tn--)
        {
            if(ta.s[tn]=='A')ta.size--;
            else if(ta.s[tn]=='B')ta.size--,reverse(ta.s+1,ta.s+ta.size+1);
        }
    }
    else if(tm>tn)
    {
        for( ;tm>tn;tm--)
        {
            if(tb.s[tm]=='A')tb.size--;
            else if(tb.s[tm]=='B')tb.size--,reverse(tb.s+1,tb.s+tb.size+1);
        }
    }

    for( ;tm&&tn;tm--,tn--)
    {
        if(eq(ta,tb))
        {
            show(ta);
            return ;
        }
        //show(ta);show(tb);
        if(ta.s[tn]=='A')ta.size--;
        else if(ta.s[tn]=='B')ta.size--,reverse(ta.s+1,ta.s+ta.size+1);
        if(tb.s[tm]=='A')tb.size--;
        else if(tb.s[tm]=='B')tb.size--,reverse(tb.s+1,tb.s+tb.size+1);
    }
    puts("-1");
    return ;
}
int main()
{
    scanf("%d",&T);
    while(T--)work();
    return 0;
}

 

C.tree

感觉出题人说的已经不能再明白了……允许我懒癌发作一次……

 

 

 

 

 或者可以直接设$f[x]$为$x$到父亲的期望步数，$g[x]$为父亲到$x$的期望步数，列出原始方程：

 

 

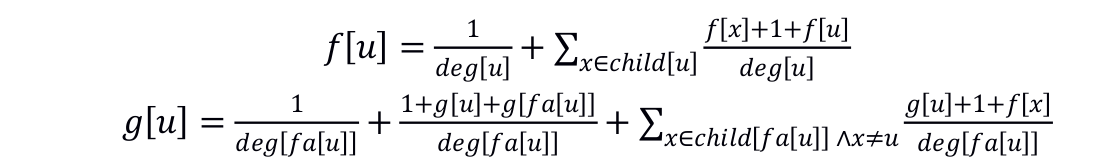
看似要高斯消元，实则可以大力化简。(同乘$deg$+把$\sum$拆成$(deg-1)\times ...$)

//既然是原题 那分我就收下了
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
	return x*f;
}
const int N=1e5+5;
int n,to[N<<1],head[N],nxt[N<<1],tot,deg[N],fa[N];
double f[N],g[N],froot;
void add(int x,int y)
{
	to[++tot]=y;
	nxt[tot]=head[x];
	head[x]=tot;
	deg[x]++;
}
void dfs(int x)
{
	f[x]=deg[x];
	for(int i=head[x];i;i=nxt[i])
	{
		int y=to[i];
		if(y==fa[x])continue;
		fa[y]=x;
		dfs(y);
		f[x]+=f[y];
	}
}
void cacl(int x)
{
	double tmp=(x==1?froot:f[x]);
	for(int i=head[x];i;i=nxt[i])
	{
		int y=to[i];
		if(y==fa[x])continue;
		g[y]=tmp-f[y]+g[x];
		cacl(y);
	}
}
void recal(int x)
{
	for(int i=head[x];i;i=nxt[i])
	{
		int y=to[i];
		if(y==fa[x])continue;
		g[y]+=g[x];
		recal(y);
	}
	g[x]+=1.0;
}
int main()
{
	/*freopen("dt.in","r",stdin);
	freopen("my.out","w",stdout);*/
	n=read();
	for(int i=1;i<n;i++)
	{
		int x=read(),y=read();
		add(x,y);add(y,x);
	}
	dfs(1);
	froot=f[1];f[1]=0;
	cacl(1);recal(1);
	for(int i=1;i<=n;i++)
		printf("%.3lf\n",g[i]);
	return 0;
}