差分标记算法笔记
差分有:一维差分、多维差分、树上差分 差分标记一般求离线区间问题!(修改完后不再修改,然后修改结束后查询)
对于带有“将一段区间内的每个数全部加上某个值”这种操作的题目,通常考虑差分原数列以简化情况,将对一段区间的操作转化为对某两个特定数的操作。
我们可以用树状数组来维护一个差分序列。差分序列的本质是通过前缀和使区间修改转换为单点修改。所以在查询的时候只要输出前缀和就可以了。
首先,给出一个问题:
给出n个数,再给出Q个询问,每个询问给出le,ri,x,要求你在le到ri上每一个值都加上x,而只给你O(n)的时间范围,怎么办?
思考一下:
如果暴力,卡一下le和ri,随随便便让你O(n^2)T成狗。
用线段树或树状数组搞一搞,抱歉,这个复杂度是O(Q logn)的,还是会T!(虽然他们解决别的题目很NB)
差分,没错,就是标题,很高兴O(n)+常数......
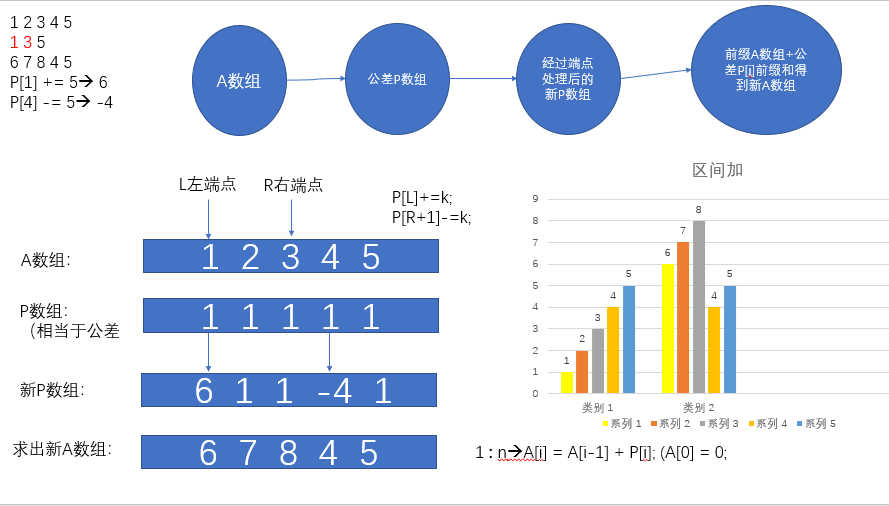
1.先另外开一个专门差分的数组(大小=题中的序列长度)
2.假如在3~8的区间上加上5,那我们在差分数组中的3位置上加上一个5(原因暂时不懂没关系,用笔先跟着模拟),再在8+1的位置上减一个5,如此操作完Q次。
3.假如我们只有这一次操作,开始统计答案,运用前置和的思想,cfi=cf[i-1]+cf[i].那么你会发现(如果你模拟了的话),在3~8的区间上,你已经使差分数组全部加上了5(推广到所有Q一起统计答案依旧正确)
4.再用O(n)的for把他们加到原序列之中去,输出!
看一下复杂度,果然:O(常数*n).
博客上看拉个题目意思大概是:
给定一个长度为N的序列: 首先进行X次操作,每次操作在Li和Ri这个区间加上一个数Ci。
然后进行Y次询问,每次询问Li到Ri的区间和。
初始序列都为0。
1<=N<=1000000,1<=X<=N, X<=Y<=N
1<=Li<=N,Li<=Ri<=N,|Ci|<=100000000000000
很多人第一眼看到这个题目第一反应都是线段树的裸题?但是本人认为线段树对于蒟蒻来说在大考中代码实现复杂,如果写的不太熟悉的话,运用大量时间去实现其是不够理智的,不过对于这个题利用差分数组解题是个不错的选择。
差分数组(差分数列):
对于一个数组A[ ],其差分数组D[i]=A[i]-A[i-1] (i>0)且D[0]=A[0]
令SumD[i]=D[0]+D[1]+D[2]+…+D[i] (SumD[ ]是差分数组D[ ]的前缀和)
则SumD[i]=A[0]+A[1]-A[0]+A[2]-A[1]+A[3]-A[2]+…+A[i]-A[i-1]=A[i]
即A[i]的差分数组是D[i], 而D[i]的前缀和是A[i]
对于“数列游戏”这题: 如果每次修改都修改从L到R的值的话,一定会TLE。
注意特殊处:这道题是先进行整体区间修改,最后才统一查询。 所以,我们只要维护一个差分数组就行了。
维护差分数组,对于将区间[L,R]加C,我们只需要将D[L]+C和D[R+1]-C 当修改完毕后,我们先求一遍差分前缀和就得到了修改后的数组A[ ],
然后再对A[ ]求一遍前缀和
这样每次查询的时候只要计算一次就可以得到结果了
总的来说差分数组适用于离线的区间修改问题,如果是在线的话应该用线段树或其他数据结构。
差分数组其实就相当于通过改变区间前端和末端与其他部分的差值,在最后进行累加的时候实行对整个区间的值的改变。
但为什么要存差值呢?————因为数列中的数满A[i]=sum{D[1]…D[i]},便于用递推求得最后的值。
差分数组是什么呢?
http://www.cnblogs.com/widsom/p/7121047.html
差分数组是前缀和的逆运算,同样运用到容斥原理
一维:
l<=r
a[l]++;
a[r+1]--;
二维:
x1<=x2&&y1<=y2
a[x1][y1]++;
a[x1][y2+1]--;
a[x2+1][y1]--;
a[x2+1][y2+1]++;
三维:
x1<=x2&&y1<=y2&&z1<=z2
a[x1][y1][z1]++;
a[x2+1][y1][z1]--;
a[x1][y2+1][z1]--;
a[x1][y1][z2+1]--;
a[x1][y2+1][z2+1]++;
a[x2+1][y1][z2+1]++;
a[x2+1][y2+1][z1]++;
a[x2+1][y2+1][z2+1]--;
是不是很简单,是不是很有规律,相信你能写出大于3维的情况了
算法笔记--差分标记
所有元素初始值为0才能这么做。
①l--r全加1
a[l]++;
a[r+1]--;
求一遍前缀和为元素本身。
求两遍前缀和为元素前缀和。
例题1:http://codeforces.com/problemset/problem/816/B
例题2:http://codeforces.com/problemset/problem/834/B
例题3:http://acm.hdu.edu.cn/showproblem.php?pid=1556
②l--r从1加到l-r+1
a[l]++;
a[r+1]-=l-r+2;
a[r+2]+=l-r+1;
求两遍前缀和为元素本身。
求三遍前缀和为元素前缀和。
因为更新时复杂度是o(1)所以复杂度为求前缀和时的o(N)。
例题:http://arc077.contest.atcoder.jp/tasks/arc077_c

树上差分(树的前缀和)
近年的NOIp,似乎对于树上差分的题目考察越来越热(参见2015年提高组 运输计划,2016年提高组 天天爱跑步)。这些题目都要知道在树上从某个点到另一个点的所有路径。但是,暴力求解这种题目经常会TLE。这种题目需要使用树上差分。在讲树上差分之前,首先需要知道树的以下两个性质:
(1)任意两个节点之间有且只有一条路径。
(2)一个节点只有一个父亲节点
这两个性质都很容易证明。那么我们知道,如果假设我们要考虑的是从u到v的路径,u与v的lca是a,那么很明显,如果路径中有一点u'已经被访问了,且u'≠a,那么u'的父亲也一定会被访问,这是根据以上性质可以推出的。所以,我们可以将路径拆分成两条链,u->a和a->v。那么树上差分有两种常见形式:(1)关于边的差分;(2)关于节点的差分。
①关于边的差分:
将边拆成两条链之后,我们便可以像差分一样来找到路径了。因为关于边的差分,a是不在其中的,所以考虑链u->a,则就要使cf[u]++,cf[a]--。然后链a->v,也是cf[v]++,cf[a]--。所以合起来便是cf[u]++,cf[v]++,cf[a]-=2。然后,从根节点,对于每一个节点x,都有如下的步骤:
(1)枚举x的所有子节点u
(2)dfs所有子节点u
(3)cf[x]+=cf[u]
那么,为什么能够保证这样所有的边都能够遍历到呢?因为我们刚刚已经说了,如果路径中有一点u'已经被访问了,且u'≠a,那么u'的父亲也一定会被访问。所以u'被访问几次,它的父亲也就因为u'被访问了几次。所以就能够找出所有被访问的边与访问的次数了。路径求交等一系列问题就是通过这个来解决的。因为每个点都只会遍历一次,所以其时间复杂度为O(n).
②关于点的差分:
还是与和边的差分一样,对于所要求的路径,拆分成两条链。步骤也和上面一样,但是也有一些不同,因为关于点,u与v的lca是需要包括进去的,所以要把lca包括在某一条链中,最后对cf数组的操作便是cf[u]++,cf[v]++,cf[a]--,cf[father[a]]--。其时间复杂度也是一样的O(n).
通过以上的描述,如果你还是不太能理解,那么以下两个题目可能可以帮助你理解:
USACO 最大流(树上差分)https://www.luogu.org/problem/show?pid=3128
NOIp2015 运输计划(树上差分+二分)https://www.luogu.org/problem/show?pid=2680


 浙公网安备 33010602011771号
浙公网安备 33010602011771号