【调和级数】codeforces 731 F. Video Cards

前言

调和级数

调和级数指的是所有正整数的倒数之和。其标准形式是：$$H_n=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}=\sum_{i=1}^{n}{\frac{1}{i}}$$
当 \(n\) 趋向于无穷大时，称之为无穷调和级数：$$\sum_{i=1}^{∞}{\frac{1}{i}}=1+\frac{1}{2}+\frac{1}{3}+...$$
数学家欧拉证明出，调和级数等于对数函数加一个常数 \(γ≈0.5772156649...\)，这个常数被称为欧拉常数。

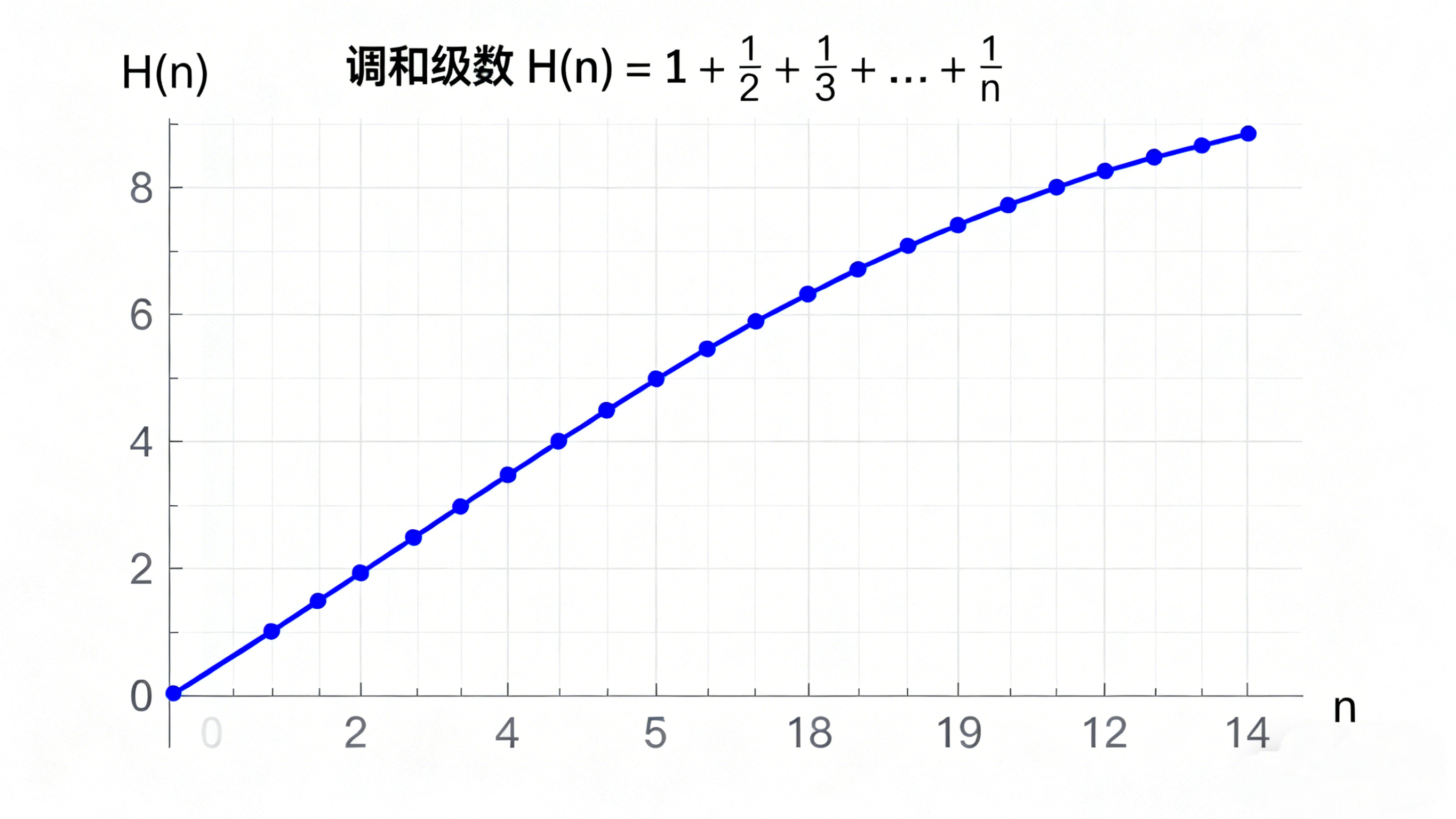
调和级数的核心特性是发散性，即虽然当项数越来越多时，虽然加的项的值的极限会趋于 \(0\)，但是调和级数的值会趋于正无穷大。尽管调和级数发散，但它发散的速度是“数学史上最慢的无穷大”之一。缓慢的程度，大致可以看以下几个例子：

• \(H_{10}≈2.93\)
• \(H_{100}≈5.19\)
• \(H_{1000}≈7.49\)
• \(H_{1000000}≈14.39\)
• \(H_{10^{100}}（一个古戈尔项之和）其值大约仅为 230.8+γ\)

调和级数在图像上类似于对数函数$$f(x) = lnx$$ 调和级数的图像如下图所示：

题目

https://codeforces.com/problemset/problem/731/F

题解

暴力的思路就是枚举步长为 \(1 \leq x \leq n\) 时的结果，此时计算的次数就为 \(n \times H_n = n \times (1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n})≈n \times lnn\)，因此是可以接受的。

另外为了更方便的枚举步长为 \(x\) 的数的个数，可以使用前缀和优化，统计到达每个数时的总个数。

时间复杂度：\(O(nlnn)\)
空间复杂度：\(O(n)\)

参考代码

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
using namespace std;

typedef long long ll;
constexpr int N = 2e5 + 7;
int n;
int a[N];
ll pre[N];

int main() {
    IOS
    ll ans = 0LL;
    int mx = 0;
    cin >> n;
    for (int i = 0; i < n; ++ i) {
        cin >> a[i];
        pre[a[i]] ++;//统计值为 a[i] 的数量
        mx = max(mx, a[i]);//维护一下数组中的最大值
    }
    sort(a, a + n);
    for (int i = 1; i <= mx; ++ i) pre[i] += pre[i - 1];
    for (int i = 0; i < n; ++ i) {
        if (i && a[i] == a[i - 1]) continue;//已经计算过就跳过
        ll res = 0LL;//计算以 a[i] 为 x 时的结果
        for (int j = 1; j * a[i] <= mx; ++ j) {
            int k = min(mx, (j + 1) * a[i] - 1);
            res += (pre[k] - pre[j * a[i] - 1]) * j * a[i];//计算值为不足 a[i] 的 j + 1 倍的数的数量
        }
        ans = max(ans, res);
    }
    cout << ans << '\n';
    return 0;
}