力扣99 恢复二叉搜索树
力扣99 恢复二叉搜索树
将二叉树错位的两个节点恢复原来的样子。
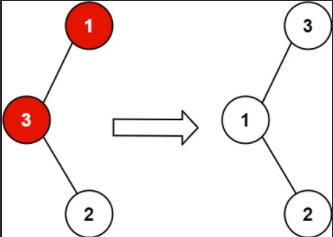
有两点需要注意:
- 中序遍历有三种方式: 显示递归,隐式递归,Mirrors, 只有最后这个能使空间复杂度为O1,但是前两个也得会。
- 节点值取值范围为Int类型所有值,初值必须设置为double类型,为Integer.MIN_VALUE-1。
茴香豆的茴字有四种写法😃,中序遍历有三种方法:
只会一种真的不大行,那就都写一遍吧 :
方法一 显示中序遍历
方法一分析:这是最笨最好想的方法,1 首先递归的方式遍历树,2 在遍历结果中寻找两个逆序对(也有可能只有一个)并记录他们的值,3重新遍历树修改值,使两个错了的值交换。
尿点1::如何在代码上统一只有一个逆序对(两个错乱的位置数值上是连续的)和两个逆序对(非连续的)两种情况?
假设一个搜索树中序遍历结果为1 2 3 4 5
如果这里是 1 3 2 4 5 则只有一个逆序对(num[i-1] 和 num[i]在 i=2的时候逆序)
如果是 1 4 3 2 5 则有两个逆序对(num[i] num[i-1]和num[j] num[j-1] 分别在i=2 和j=3的时候逆序)
同理 5 2 3 4 1这也有两个逆序对
遍历的时候判断是否产生逆序,就需要当前节点值(较小者)和其前驱节点值,但是在这种笨方法下,遍历的方式为遍历列表。,如何统一两种情况呢?(其实就是存最左边和最右边),最右边需要时刻更新,出现逆序对就改,最左边第一次逆序改,只改一次。为了将逻辑写成循环结构:
首先设置 x y 存两个逆序的变量(不妨让x存 nums[i] y存nums[i+1])
循环遍历数组,每次遍历,
1 首先先更新最右的值y,
2 选择性更新最左的值x(其实只改一次):若x一次都没改过,需要改动,今后不再改动。若改动过了,说明xy都改对了,直接break即可。
伪代码:
int x =-1 ,int y=-1;
for(int i = 0;i<n-1;i++){
if(num[i]>num[i+1]){
y=nums[i+1];//由于不知道何时结束逆序,出现了就得更新最右边的值
if(x==-1){
x = nums[i];//只有第一次逆序的左边才是最左边,x为初值的时候更新,其他时候不更新。
}else{
break;//出现第二次逆序,就可以break了
}
}
}
尿点2 :x y的初值,由于val值为全体int,所以x y的初值不能为int的任何值,所以需要double x y 为Integer.MIN_VALUE-1,当时1900个例子有一个没跑通就是因为这个。。。
代码如下:
class Solution {
public void recoverTree(TreeNode root) {
List<Integer> num = new ArrayList<>();
//中序遍历函数
inorder(root,num);
//寻找错位的两个节点值,并返回这个值的函数
int[] a = findtwo(num);
//交换这两个值的函数
swap(a[0],a[1],root);
}
//简单的中序遍历
void inorder(TreeNode root,List num){
if(root==null)return;
inorder(root.left,num);
num.add(root.val);
inorder(root.right,num);
}
//尿点一和尿点二的实现
int[] findtwo(List num){
double x = Integer.MIN_VALUE-1;double y = Integer.MIN_VALUE-1;
int n = num.size();
for(int i =0;i<n-1;i++){
if((Integer)num.get(i)>(Integer)num.get(i+1)){
y = (Integer)num.get(i+1);
if(x==Integer.MIN_VALUE-1){
x = (Integer)num.get(i);
}else{
break;
}
}
}
return new int[]{(int)x,(int)y};
}
//交换函数
void swap(int x,int y ,TreeNode root){
//其实并不是真的swap,单纯的改值而已,如果是x就改成y,如果是y就改成x
if(root==null)return;
if(root.val==x){
root.val=y;
}else if(root.val==y){
root.val=x;
}
swap(x,y,root.left);
swap(x,y,root.right);
}
}
复杂度分析
时间复杂度:O(N)
空间复杂度:O(N)
方法二 隐式中序遍历
显示手动维护一个栈,不用纯纯递归的方式,不需要数组(这样好废物)。
就是一个变型的隐中序遍历,由于一般的隐遍历我不会写,这个也无从下手,所以要记住这个套路。
其实他就是一个mirros,只不过通过栈记录了原路,历史扫描过的节点。
class Solution {
public void recoverTree(TreeNode root) {
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode pre = null;
TreeNode x = null;
TreeNode y = null;
//循环条件有两个 ,栈不空,root不空 只要满足一个就说明没完事。
while(!stack.isEmpty()||root!=null){
//找到该root的最左侧节点,就是该root的第一个遍历的节点。
while(root!=null){
stack.push(root);
root=root.left;
}
root = stack.pop();
/////////////////////////////////////////业务处理和方法一一样
if(pre!=null&&pre.val>root.val){
y = root;
if(x==null){
x = pre;
}else{
break;
}
}
pre = root;
////////////////////////////////////////////
//把最左侧末梢的结点右结点变成root。(这使得右节点树也获得了完全同左子树的入栈的操作)
root = root.right;
}
swap(x,y);
}
void swap(TreeNode x,TreeNode y){
int temp = x.val;
x.val = y.val;
y.val = temp;
}
}
复杂度分析
时间复杂度 :O(N),节点个数
空间复杂度: O(H) 高度
方法三 Mirrors法中序遍历
不止一次见到mirrors了,每次都不会写,这次记一下吧!
由于方法二,root = root.right 进入下一轮while后 如果是null 我们直接pop,mirrors是对这个过程的化简,事先把触发pop的条件找到,也就是找到了 这个节点在遍历顺序上的前一个节点。
就是root的左子树的最右节点(如果root存在左子树的话,root一定先入栈了,等左子树最右节点遍历完再pop)
比较发生在每一次pop的时候,也就是每一次遍历完左子树的时候。(中序遍历 左 中 右)
在mirros遍历过程中,有两处:
1 root.left==null 此时root为遍历到的最小值,需要pop
2 root.left!=null,但是prodecessor.right=root,此时prodecesser
class Solution {
public void recoverTree(TreeNode root) {
TreeNode x = null;TreeNode y = null;TreeNode predecessor = null;TreeNode pre =null;
while(root!=null){
if(root.left!=null){
//找到该root的前驱节点。
predecessor = root.left;
while(predecessor.right!=null&&predecessor.right!=root){
predecessor=predecessor.right;
}
if(predecessor.right==null){
predecessor.right = root;
root=root.left;
}else{
//第二次遇见root,一定是要pop了
if(pre!=null&&pre.val>root.val){
y = root;
if(x==null){
x = pre;
}
}
pre = root;
predecessor.right=null;
root = root.right;
}
}else{
//左子树都没有,一定pop
if(pre!=null&&pre.val>root.val){
y = root;
if(x==null){
x =pre;
}
}
pre = root;
root = root.right;
}
}
swap(x,y);
}
void swap(TreeNode x,TreeNode y){
int temp = x.val;
x.val = y.val;
y.val = temp;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号