Leetcode120 三角形最小路径

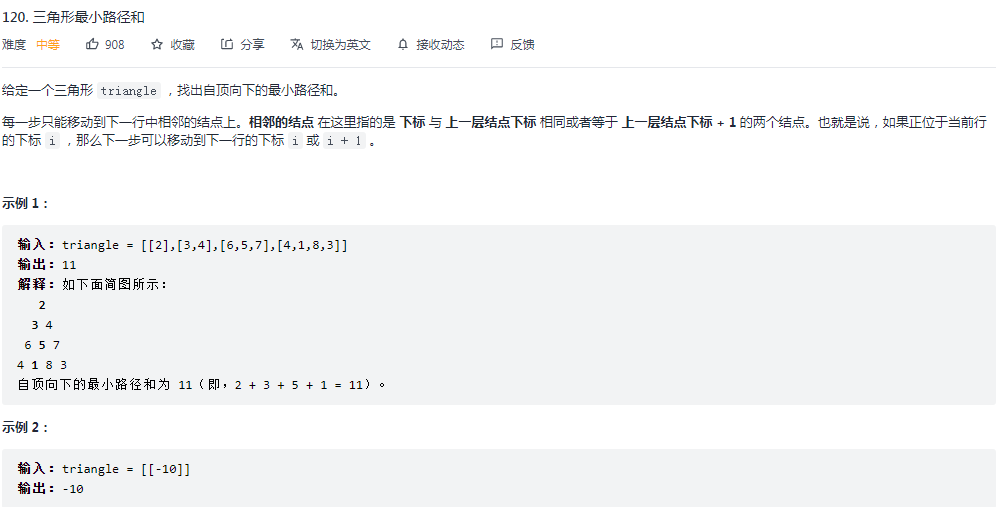
LeetCode 120. 三角形最小路径

​ 原题链接

思路：思路是不可能有的，怎么会能有思路呢，不过给我答案我看了思路以后很快就能复写出来，而且感觉还好，，，，

仔细分析，他就是个需要用到动态规划的问题！！

而且是个典型的多决策问题、、、

我一开始纠结与他并不是无后效性的，后来看了答案发现，他真的是无后效性的。

1

2 3

5 7 8

2 8 7 9

不就是这样的三角形么，构建map使得map上的i行j列就表示 i j 的最短距离。

根据提上的限定条件，最左边和最右边都是唯一确定的，中间的有i-1 j 和i-1 j-1来确定。

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        int[][] map = new int[n][n];
        map[0][0] = triangle.get(0).get(0);
        
        for(int i = 1;i<n;i++){
    map[i][0]=triangle.get(i).get(0)+map[i-1][0];
           
            for(int j = 1;j<i;j++){map[i][j] = Math.min(map[i-1][j],map[i-1][j-1])+triangle.get(i).get(j);            
            }   
            
    map[i][i]=triangle.get(i).get(i)+map[i-1][i-1];        
        }
        
        int min = Integer.MAX_VALUE;
        
        for(int i = 0;i<n;i++){
        min = Math.min(min,map[n-1][i]);
        }
        
        return min;
    }
    }

​ 后来可以考虑倒着走，而且在原来的列表里改代码。这样似乎更简洁，但是是get 和set 列表，速度会慢一些。。。。。。

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
      for(int i = triangle.size()-2;i>=0;i--){
          for(int j = 0;j<=i;j++){
triangle.get(i).set(j,triangle.get(i).get(j)+Math.min(triangle.get(i+1).get(j),triangle.get(i+1).get(j+1)))  ;
          }         
      }
      return triangle.get(0).get(0);
    }
    }

再后来 为了节省空间复杂度，我们把int[][]的结构变成了int []这样空间复杂度变成了O（n）

代码如下：

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
    int[] map = new int[n];
    for(int i = 0;i<n;i++){
      map[i]=triangle.get(n-1).get(i);
    }
      for(int i = n-2;i>=0;i--){
          for(int j = 0;j<=i;j++){
        map[j] = triangle.get(i).get(j)+Math.min(map[j],map[j+1]);          
          }         
      }
      return map[0];
    }
    }

中间迭代的部分我又马虎了，，，，，哎 断点调式了一个小时，折磨死我啦。下回能不能认真一点，，，，，，

虽然每次都有问题，但是所有问题都找出来了。。。。。。