力扣198 打家劫舍

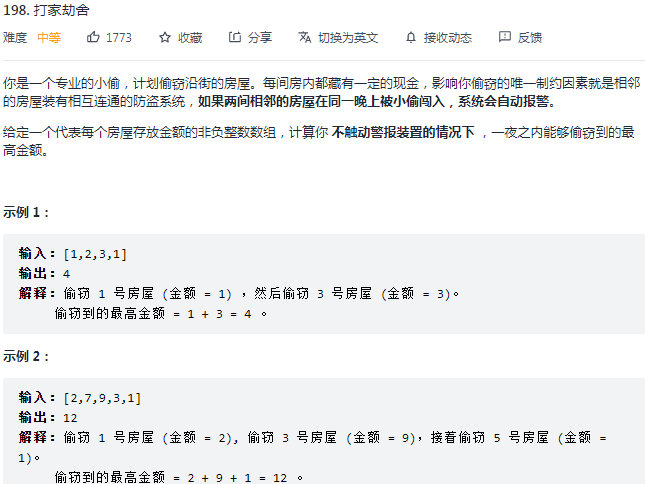
力扣 198.打家劫舍

题目类型：动态规划，类似爬楼梯，但这道题更好，爬楼梯虽然写了很多解法，但是总给人一种只能解决斐波那契数列的问题（其实是斐波那契满足了动态规划的某些条件）。而这道题让我知道了动态规划问题的意义。

多决策问题时候用动态规划，什么是多决策问题呢？

阶段：把所给求解问题的过程恰当地分成若干个相互联系的阶段，以便于求解，过程不同，阶段数就可能不同．描述阶段的变量称为阶段变量。在多数情况下，阶段变量是离散的，用k表示。此外，也有阶段变量是连续的情形。如果过程可以在任何时刻作出决策，且在任意两个不同的时刻之间允许有无穷多个决策时，阶段变量就是连续的 [6] 。

状态：状态表示每个阶段开始面临的自然状况或客观条件，它不以人们的主观意志为转移，也称为不可控因素。在上面的例子中状态就是某阶段的出发位置，它既是该阶段某路的起点，同时又是前一阶段某支路的终点 [6] 。

无后效性：我们要求状态具有下面的性质：如果给定某一阶段的状态，则在这一阶段以后过程的发展不受这阶段以前各段状态的影响，所有各阶段都确定时，整个过程也就确定了。换句话说，过程的每一次实现可以用一个状态序列表示，在前面的例子中每阶段的状态是该线路的始点，确定了这些点的序列，整个线路也就完全确定。从某一阶段以后的线路开始，当这段的始点给定时，不受以前线路（所通过的点）的影响。状态的这个性质意味着过程的历史只能通过当前的状态去影响它的未来的发展，这个性质称为无后效性 [6] 。

决策：一个阶段的状态给定以后，从该状态演变到下一阶段某个状态的一种选择（行动）称为决策。在最优控制中，也称为控制。在许多问题中，决策可以自然而然地表示为一个数或一组数。不同的决策对应着不同的数值。描述决策的变量称决策变量，因状态满足无后效性，故在每个阶段选择决策时只需考虑当前的状态而无须考虑过程的历史 [6] 。

决策变量的范围称为允许决策集合 [6] 。

策略：由每个阶段的决策组成的序列称为策略。对于每一个实际的多阶段决策过程，可供选取的策略有一定的范围限制，这个范围称为允许策略集合

那这个分析之后

f(0) = 0;f(1)=1;f(n) = Max(f(n-1),f(n-2)+num[n]);

那这个就可以用滚动数组来写了

class Solution {  
    public int rob(int[] nums) {
        int len = nums.length;
        int[] state = new int[2];
        if(len==0) return 0;
        if(len==1) return nums[0];
        state[0] = 0;
        state[1] =nums[0];
        int temp = 0;
        for(int i=1;i<len;i++){
            temp = state[1];
            state[1] = Math.max(state[1],state[0]+nums[i]);
            state[0] =temp;        
        }
        return state[1];
    }  
}