位似

位似图形指的是两个相似并且对应边平行的图形，它们对应点连线交于一点，称为位似中心

位似具有以下三个性质：

1. 两个图形相似

2. 两图形对应点连线交于一点

3. 两图形对应边平行

满足 \(3\) 则可判定为位似，当然圆之间的都是位似的。需要注意的是 \(1+2\) 并不能判定位似，只能在交于一点 \(O\) 后，满足 \(\frac{OX}{OX'}=\frac{OY}{OY'}=...\) 来判定（本质也是平行）

位似比较重要的知识点的是：两个相切的圆关于它们的切点位似（也经常用来证明圆相切）（所以说，过切点作直线交两圆于 \(X,Y\) ，那么过 \(X,Y\) 的切线平行）

关于圆的位似中心还有一些结论：

1. 两圆的内外位似中心与它们的两圆心构成了调和点列。

2. 三圆两两的外位似中心共线。也可以将其中两个改为内位似中心。

3. 关于外位似中心既有位似关系，也有反演关系（详见反演）

以及三角形构型中还有很多的位似，比如九点圆就是外接圆位似的结果，以及内切圆与旁切圆的位似，和切点三角形和旁心三角形的位似，等等，可以在具体的模块看到。

例1

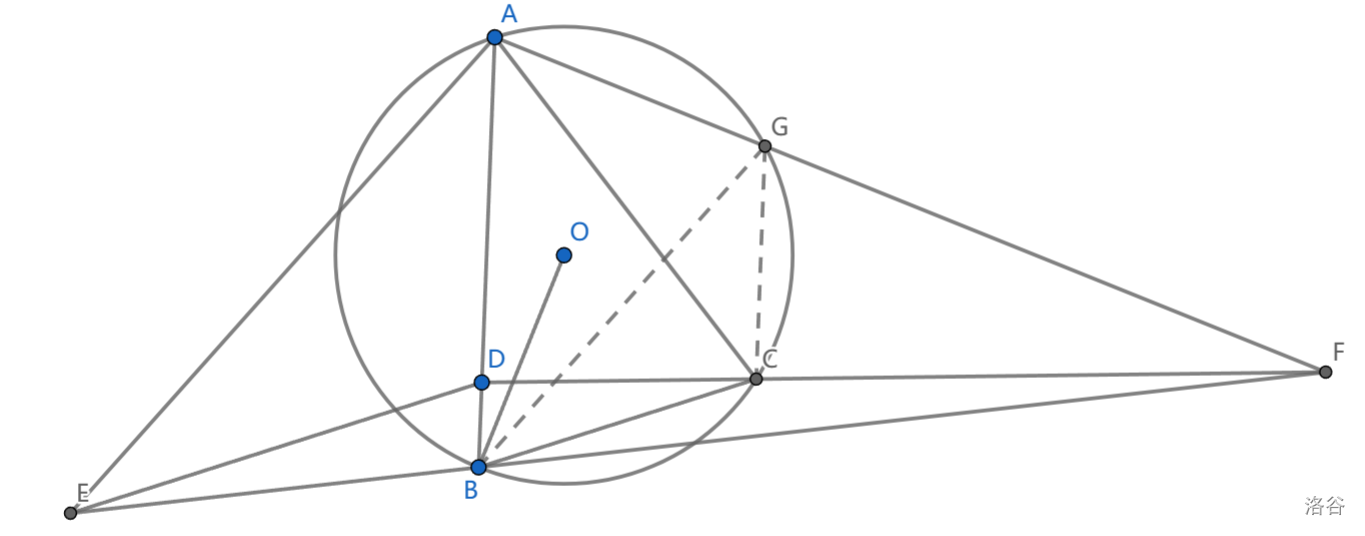
如图，\(\triangle ABC\) 满足 \(AB=AC\) ， \(D\) 是 \(AB\) 上一点， \(DE // BC\) ，且点 \(E\) 满足 \(\angle BAE=\angle BAC\) ，过 \(A\) 作与 \(OB\) 垂直的直线交 \(DC\) 于 \(F\) ，求证：\(EBF\) 共线

一定要注意图形的生成顺序，直线 \(AF\) 与点 \(D\) 是不相关的

想法是，已有 \(DE//BC\) ，要证它们连线交于一点，可以借助位似，我们构造 \(CG//AB\) 交 \(AF\) 于 \(G\)

可以看到 \(\angle BAF=\angle ABC\) ，从而 \(ABCG\) 是等腰梯形，四点共圆

则 \(\angle BGF=\pi-\angle AGB=\pi-\angle ACB=\angle EAF\) （最后一个等号由导角得到）

从而 \(BG//AE\) ，知 \(\triangle ADE,\triangle GCB\) 位似， \(F\) 为位似中心

例2

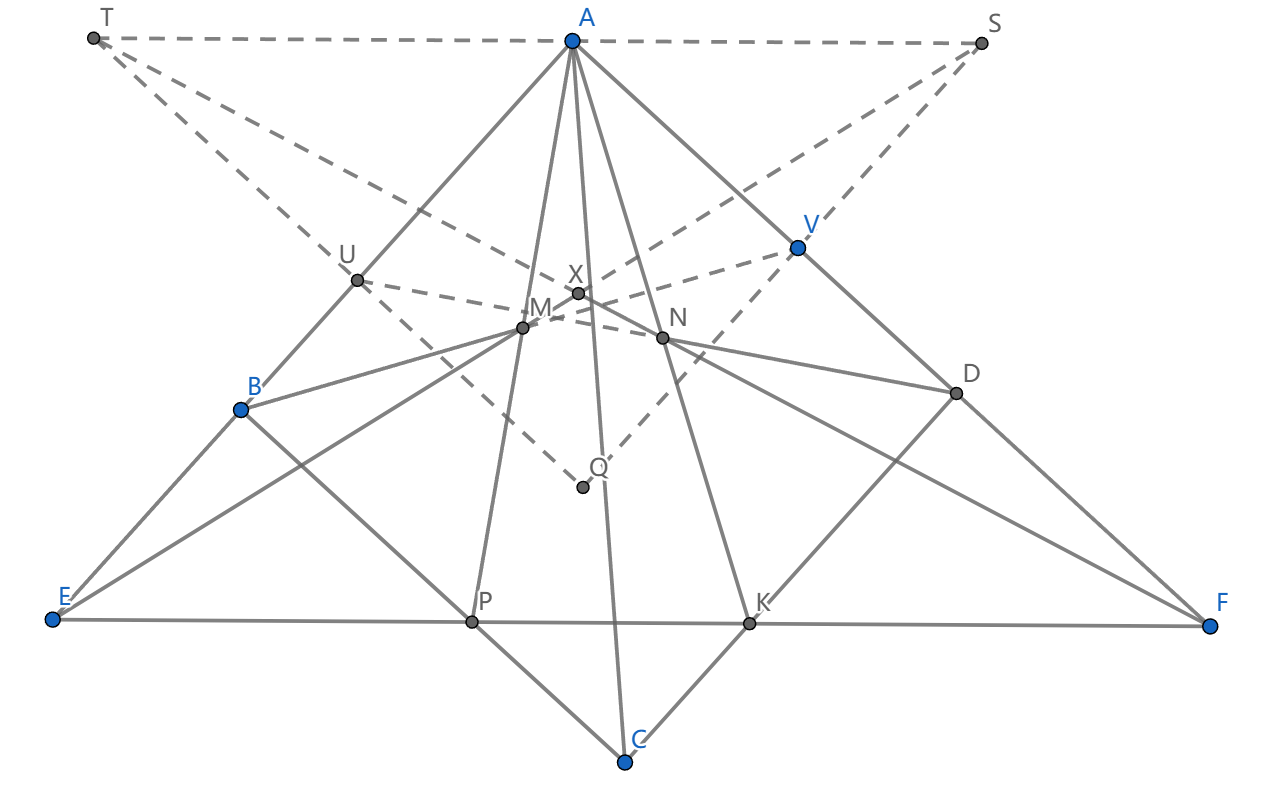
如图，直线 \(EF\) 与 平行四边形 \(ABCD\) 四边交于 \(E,P,K,F\) ， \(M,N\) 在 \(AP,AK\) 上，满足 \(\angle ABM=\angle ADN\) ，直线 \(EM,FN\) 交于 \(X\) ，证明： \(\angle BAC=\angle DAX\)

我们延长 \(BM\) 交 \(AD\) 于 \(V\) ，延长 \(DN\) 交 \(AB\) 于 \(U\) ，于是 \(BDUV\) 共圆，再延长 \(EM,FN\) 与过 \(A\) 作 \(EF\) 的平行线交于 \(S,T\) ，然后

\(\frac{SM}{EM}=\frac{AM}{PM}=\frac{VM}{BM}\) ，所以 \(SV//AB,TU//AD\)

延长 \(TU,SV\) 交于 \(Q\) ，然后 \(\triangle QST,\triangle AEF\) 位似。额外地，平行四边形 \(AUQV\) 与 \(ABCD\) 也位似，所以 \(\angle DAQ=\angle BAC\)

我们看到 \(X=ES\cap FT\) 是 \(\triangle QST,\triangle AEF\) 的位似中心，所以 \(AXQ\) 共线，完成了证明。

例3

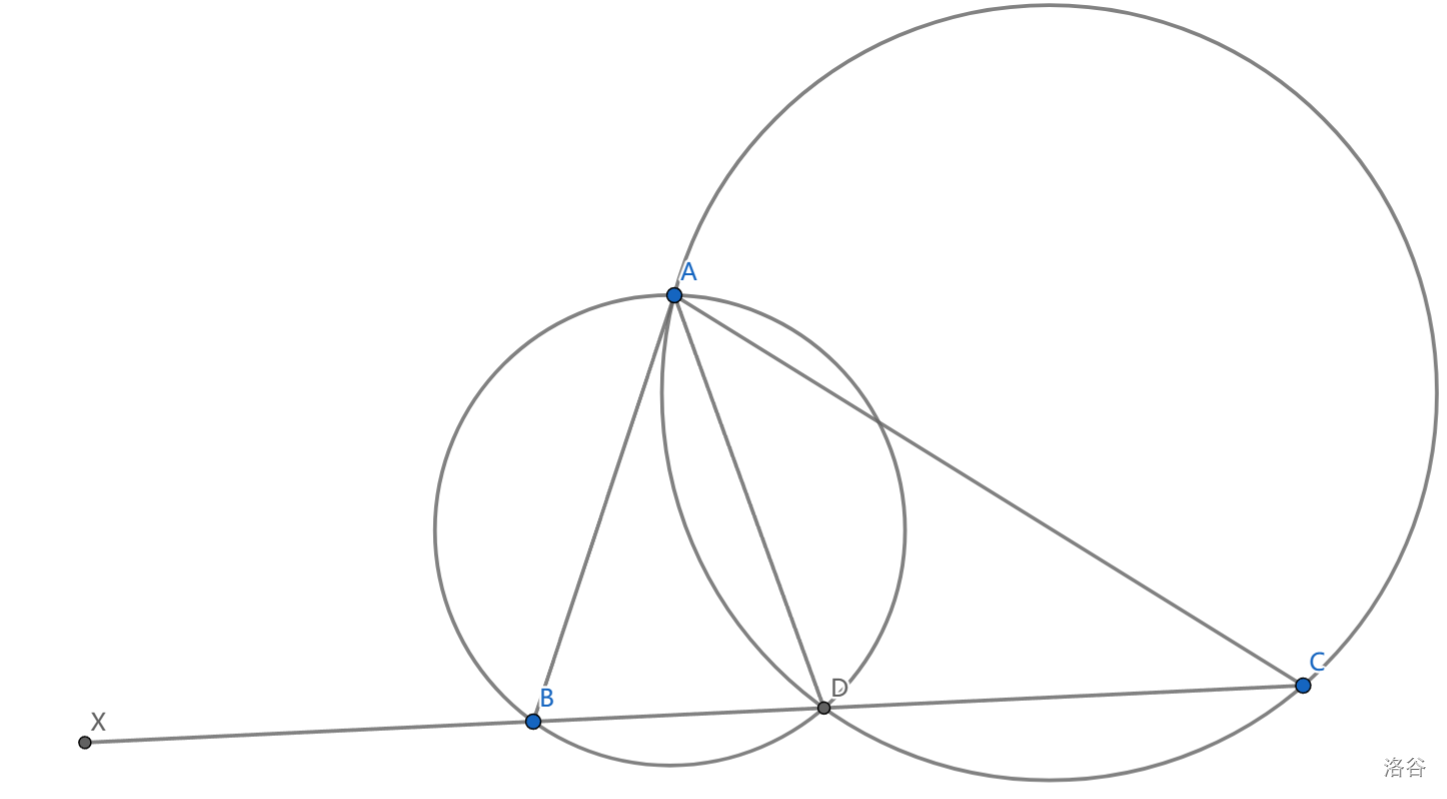
作 \(\triangle ABC\) 的三条内角平分线 \(AD,BE,CF\) ，设 \(X\) 是 \(\odot(ABD),\odot(ACD)\) 的外位似中心，同理定义 \(Y,Z\) ，证明： \(XYZ\) 共线

关键是发现 \(X\) 在 \(BC\) 上

设 \(XD\) 交两圆于 \(B',C'\) ，则有位似对应 \(B'\sim D,D\sim C'\) ，则弧 $B'D\sim $ 弧 \(DC'\) ，有 \(\angle B'AD=\angle C'AD\)

显然，过 \(D\) 的两圆割线满足这一条件的仅 \(BDC\) 一条，从而 \(B'=B,C'=C\) ，从而 \(X\) 在 \(BC\) 上

有 \(\frac{XB}{XC}=\frac{XB}{XD}\cdot \frac{XD}{XC}=(\frac{AB}{AC})^2\) ，从而 \(\prod\limits_{cyc}\frac {XB}{XC}=1\) ，由梅涅劳斯定理知 \(X,Y,Z\) 共线

例4

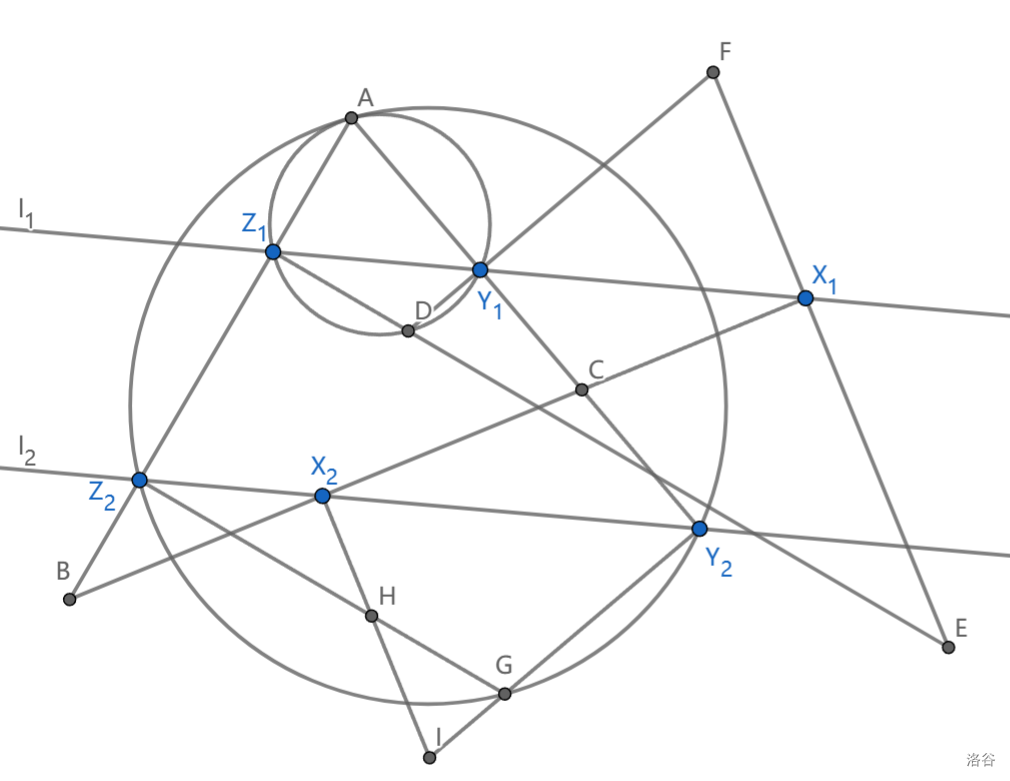
如图，平行线 \(l_1,l_2\) 与 \(\triangle ABC\) 三边分别交于 \(X_i,Y_i,Z_i(i=1,2)\) ，过 \(X_i\) 作 \(BC\) 垂线，过 \(Y_i\) 作 \(AC\) 垂线，过 \(Z_i\) 作 \(AB\) 垂线，分别构成三角形 \(\triangle_1,\triangle_2\) ，证明： \(\triangle_1,\triangle_2\) 的外接圆相切

如果你看到垂直条件下意识发现 \(l_1,l_2\) 的本质是西姆松线，这道题就好做了

显然 \(\triangle AY_1Z_1,\triangle AY_2Z_2\) 位似，并且 \(AY_1Z_1D,AY_2Z_2G\) 共圆，其中 \(D,G\) 关于 \(\triangle AY_1Z_1,\triangle AY_2Z_2\) 的西姆松线 \(l_1,l_2\) 平行 ，从而它们也是位似对应点

导致 \(Y_1D//Y_2G\) 即 \(DF//GI\) ，从而 \(\triangle DEF,\triangle GHI\) 位似，它们的外接圆相切

例5

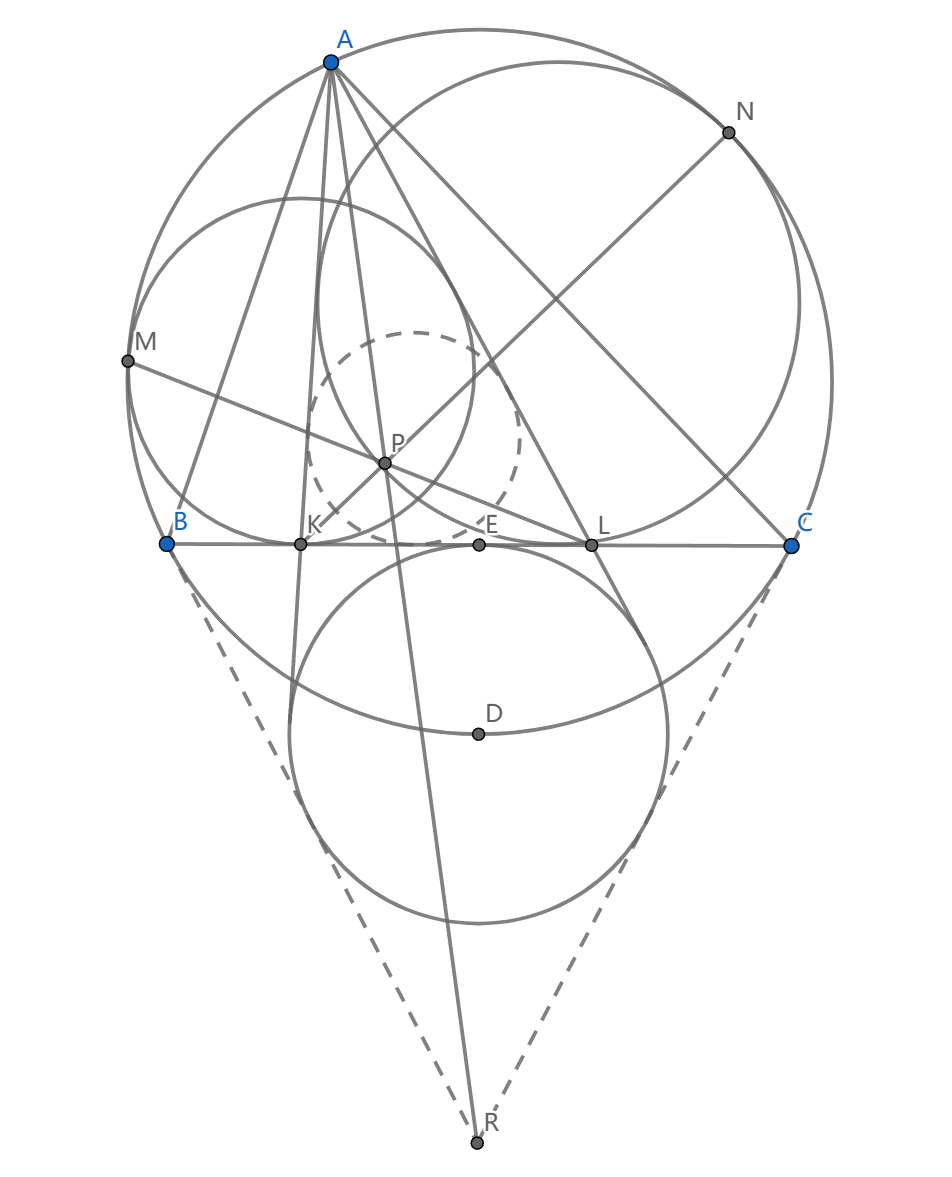
如图， \(D\) 是弧中点， \(E\) 是中点， \(c\) 以 \(D\) 为圆心以 \(DE\) 为半径。过 \(A\) 作 \(c\) 两条切线交 \(BC\) 于 \(K,L\) ，圆 \(c_1\) 与 \(AL,BL\) 相切并与 \((ABC)\) 切于点 \(M\) ，圆 \(c_2\) 与 \(AK,CK\) 相切并与 \((ABC)\) 切于点 \(N\) ， \(P=ML\cap NK\) ，求证： \(\angle BAP=\angle CAE\)

这个问题利用了三圆两两位似中心（三外或一外二内）共线的性质，作 \(AKL\) 内切圆 \(c_0\) ，我们看到 \(M\) 是 \(c_1\) 与 \((ABC)\) 的外位似中心， \(L\) 是 \(c_0\) 与 \(c_1\) 的外位似中心（公切线交点），所以 \(c_0\) 与 \((ABC)\) 的外位似中心在 \(ML\) 上

同理这个位似中心还在 \(KN\) 上，所以就是点 \(P\) 。我们要证 \(AP\) 是共轭中线，所以作过 \(B,C\) 的切线，发现这是 \(c\) 与 \((ABC)\) 的公切线。

事实上，我们过 \(C\) 作 \(c\) 切线 \(CQ\) ，我们看到 \(\angle BCD=\frac 12A\) ，然后 \(CD\) 平分 \(\angle BCQ\) （因为 \(BC\) 也是切线），所以 \(\angle BCQ=A\) ，说明 \(CQ\) 也是 \((ABC)\) 切线

现在 \(Q\) 是 \(c\) 与 \((ABC)\) 外位似中心， \(P\) 是 \(c_0\) 与 \((ABC)\) 外位似中心， \(A\) 是 \(c\) 与 \(c_0\) 外位似中心（注意切线 \(AK,AL\) ），他们共线，这就完成了证明。