密克构型

三角形中的密克点

如图，\(D,E,F\) 在 \(BC,AC,AB\) 上，则 \((AEF),(BDF),(CDE)\) 交于一点（纯导角）

例1

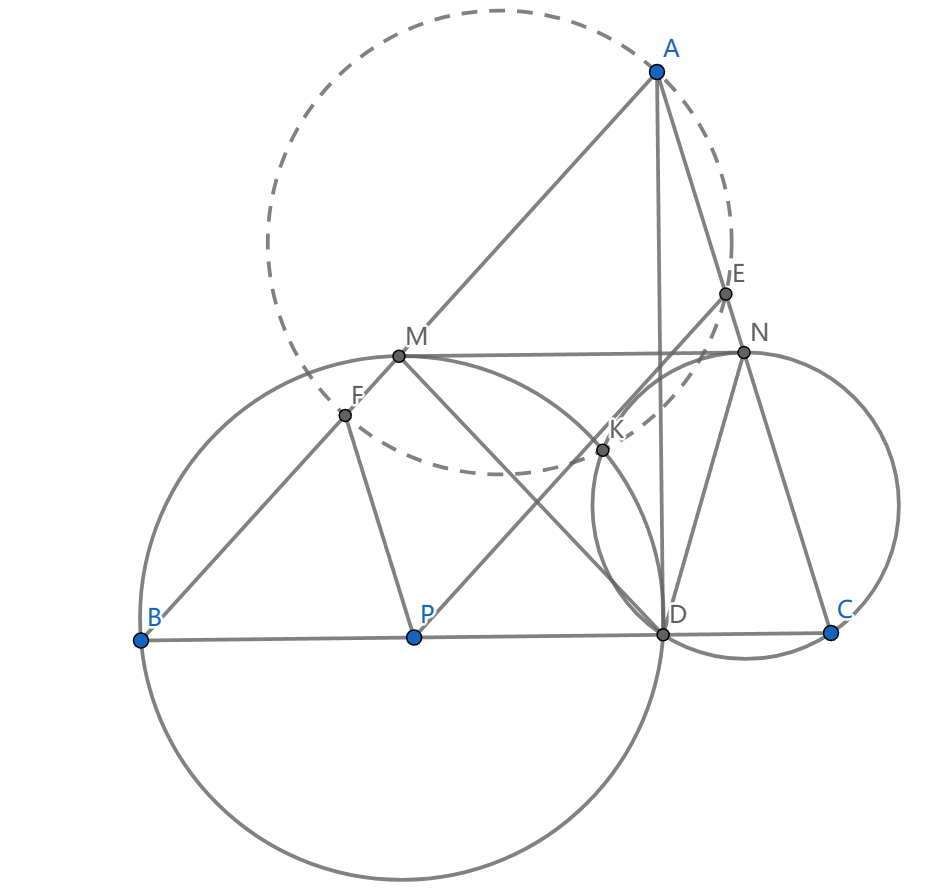
如图， \(AD\) 是高， \(M,N\) 是中点， \(K=(BDM)\cap (CDN)\) ， \(P\) 在 \(BC\) 上，过 \(P\) 作 \(AB,AC\) 平行线交 \(AC,AB\) 于 \(E,F\) ，求证： \(KEAF\) 共圆。

有很多做法，其中一个是利用相似对应来处理 \(\frac{BF}{FA}=\frac{AE}{EC}\) 的条件，如果我们证明了 \(\triangle KBA(F)\sim\triangle KAC(E)\) ，就立即有 \(\angle KEA=\angle KFB\) ，从而证明了命题。

所以只要 \(\angle KAC=\angle KBA\) 。根据密克构型会有 \(AMKN\) 共圆，所以 \(\angle NAK=\angle NMK\) ，我们想要 \(\angle NMK=\angle KBM\) ，只要说 \(MN\) 是 \((BDM)\) 切线，根据 \(\angle NMD=\angle MDB=\angle MBD\) 可得。

完全四边形中的密克点

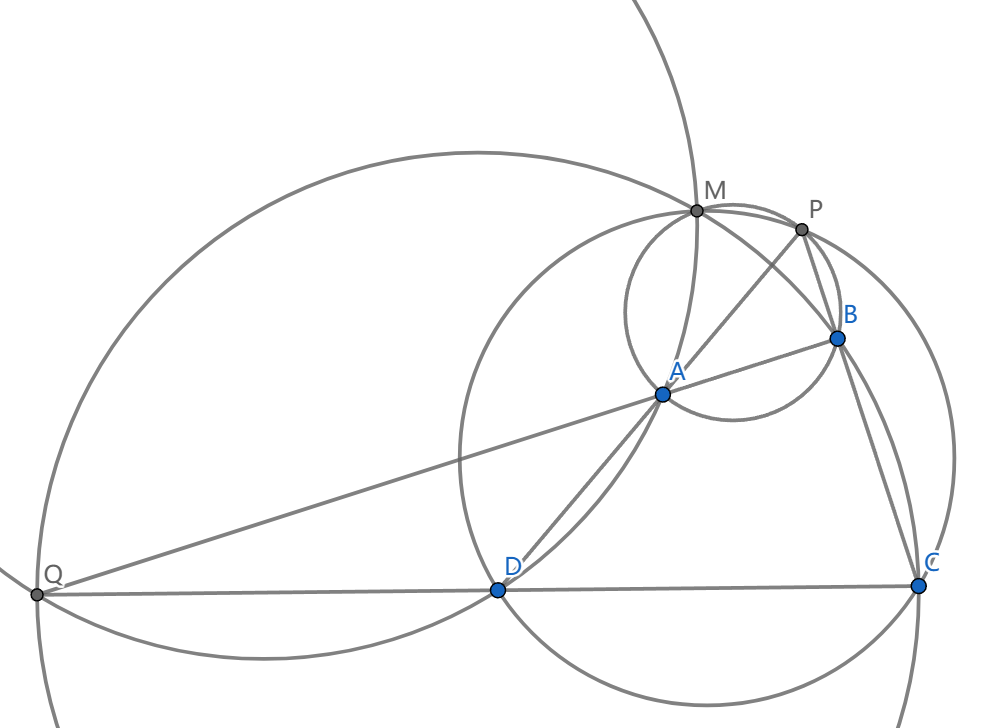
完全四边形的四边围出的四个三角形外接圆共点（纯导角）

下面这个定理在国内被称作牛顿线定理，但我们不会用牛顿的证明，而是后来的高斯-波登米勒给出的更加简单且有效的证明：

如图，以完全四边形三条对角线为直径的圆共轴，根轴经过上述四个三角形每一个的垂心

任取一个垂心 \(H_1\) ，显然它是 \(QC,AC,PQ\) 为直径的圆的根心，它还是 \(BC,BD,AC\) 为直径的圆的根心，对其它垂心同理分析就证毕。

我们还有以下的一些结论：

1. 密克点与四个外心共圆（利用旋转相似，也可解释为导角）

2. 密克点到四边的垂足共线，这条线垂直于牛顿线 （西姆松定理，后者需要一些导角）

圆内接四边形的密克点有比较特殊的性质，我们做一个介绍。

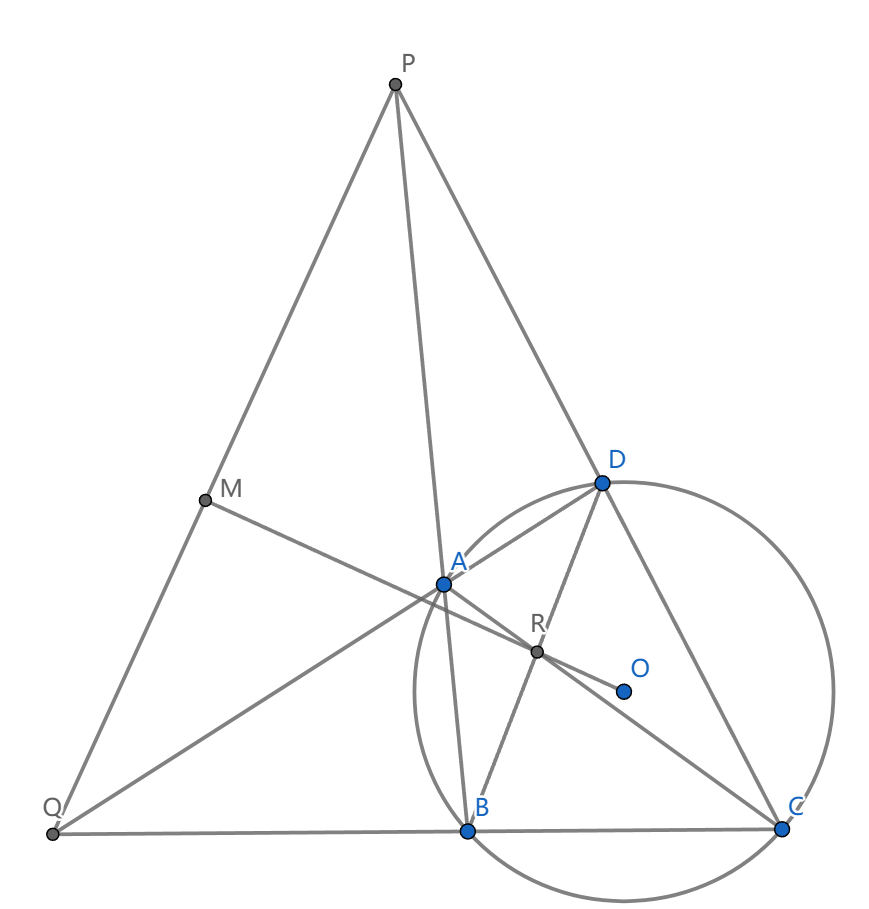
如图，圆内接四边形 \(ABCD\) 的密克点在对角线 \(PQ\) 上，与对角线交点 \(R\) 互为 \((ABCD)\) 的反演对应点

一些简单的导角配合 \(Brocard\) 定理就能给出这个结果。我们还有一些有趣的结果（只对圆内接四边形的密克点生效）：

1. \(M\) 在 \((OAC),(OBD)\) 等圆上

2. \(MO\) 平分 \(\angle AMC,\angle BMD\)

最后说一句：显然密克点和旋转相似是非常相关的。

例1

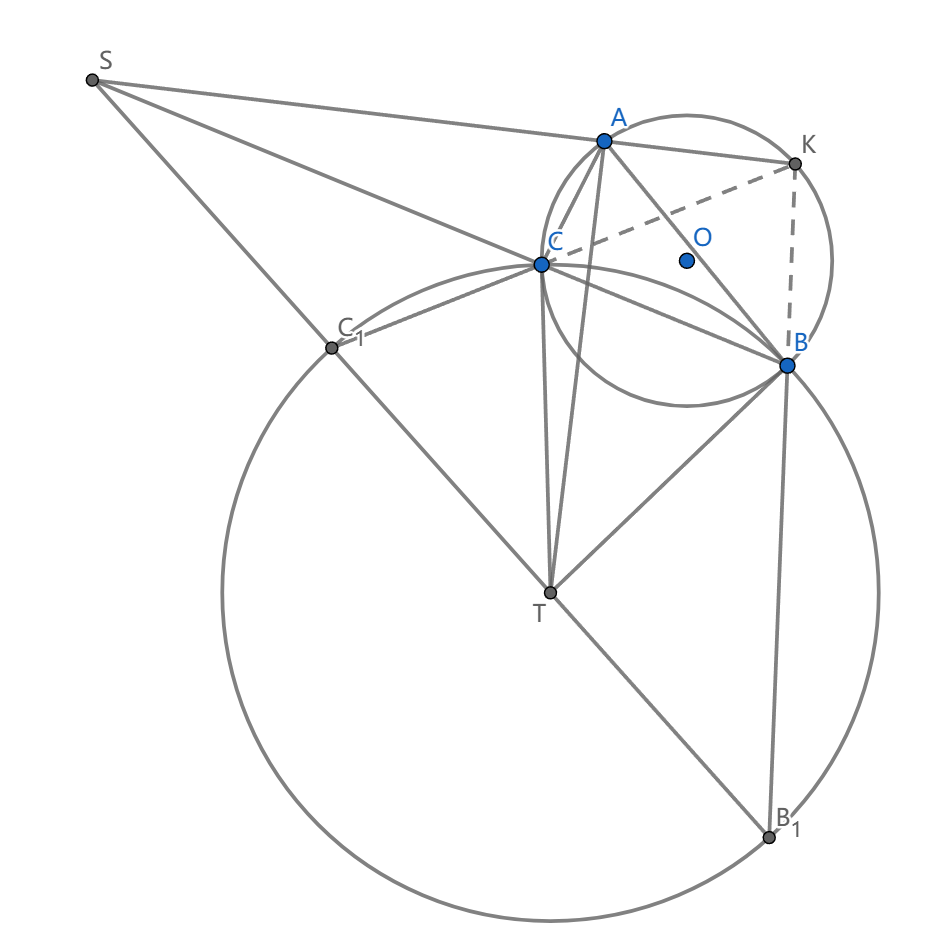
如图，\((ABC)\) 过 \(B,C\) 的切线交于点 \(T\) ，射线 \(BC\) 上一点 \(S\) 满足 \(AS\perp AT\) ，点 \(B_1,C_1\) 在射线 \(S,T\) 上，满足 \(B_1T=BT=C_1T\) ，证明： \(\triangle ABC\sim\triangle AB_1C_1\)

设 \(K=BB_1\cap CC_1\) ，我们看到 \(\angle BKC=\pi-\angle B_1-\angle C_1=\angle TBC=\angle BAC\) ，所以 \(K\) 在 \((ABC)\) 上

由 \(BB_1C_1C\) 内接于圆，它的密克点 \(A'\) 在 \((KBC)\) 上且满足 \(\angle TA'S=Rt\angle\) ，而 $\angle TAS=Rt\angle $ 是已知的，所以 \(A=A'\) 是 \(BB_1C_1C\) 的密克点，这就证毕。

例2

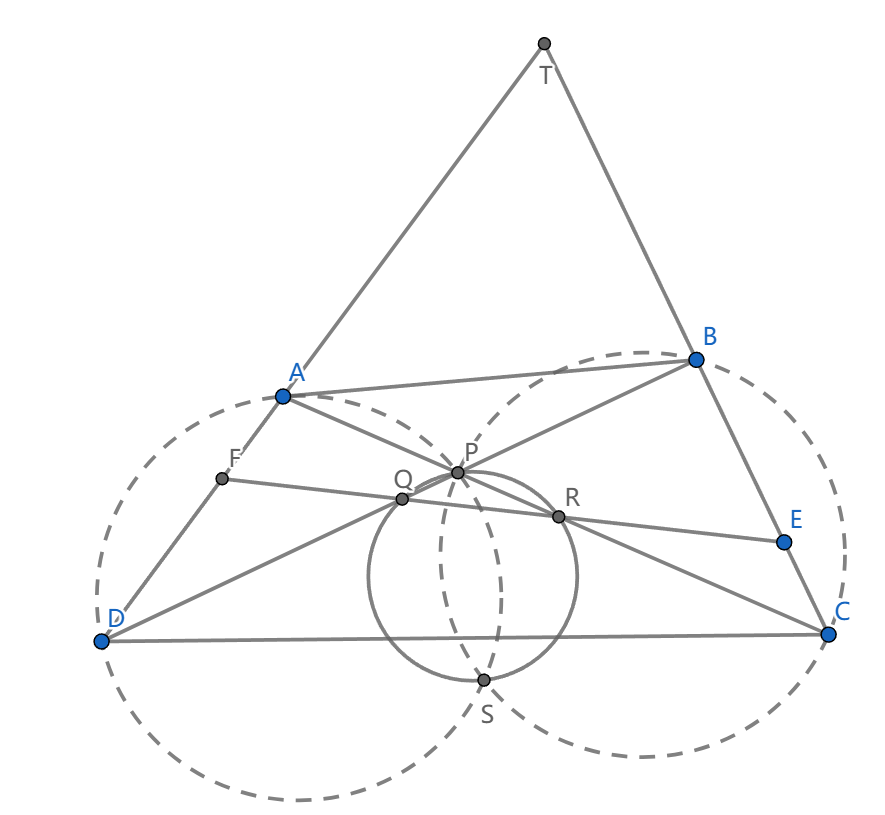
如图，四边形 \(ABCD\) 满足 \(BC=DA\) ，边 \(BC,DA\) 上动点 \(E,F\) 满足 \(BE=DF\) ，设 \(P=AC\cap BD,Q=BD\cap EF,R=AC\cap EF\) ，求证： \((PQR)\) 过不同于 \(P\) 的定点。

这个定点是 \(\odot(PAD)\cap \odot(PBC)\) ，或者说，我们证明 \(ADBC\) 的密克点 \(S\) 也是 \(ARQD\) 的密克点

我们看到 \(\triangle SAD\cong\triangle SBC\) 中 \(F,E\) 是全等对应点，从而 \(\angle ASC=\angle FSE=\pi- T\) ，所以 \(TFSE\) 共圆

那么 \(S\) 是 \(FACE\) 的密克点，然后 \(ASRF\) 共圆，所以 \(S\) 也是 \(ARQD\) 的密克点。

例3

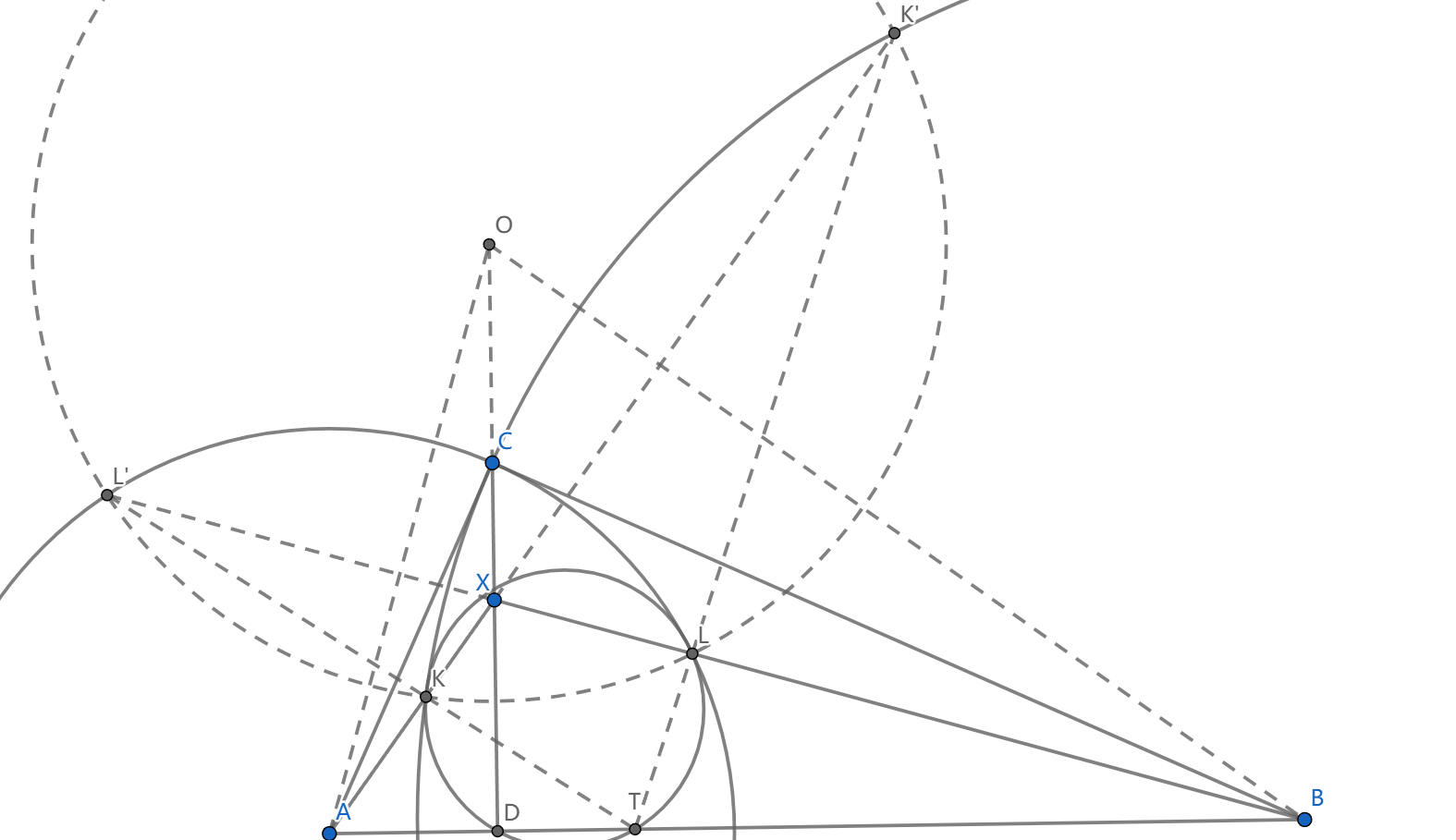
如图， \(\triangle ABC\) 是直角三角形， \(CD\) 是高， \(X\) 在 \(CD\) 上， \(AX\) 上的点 \(K\) 满足 \(BK=BC\) ， \(BX\) 上的点 \(L\) 满足 \(AL=AC\) ， \((DKL)\) 与 \(BC\) 交于点 \(T\ne D\) ，求证： \(CT\) 平分 \(\angle ACB\)

这个问题远比看上去难。我们添加 \(c_a,c_b\) 两个圆，以 \(A,B\) 为圆心，以 \(AC,BC\) 为半径，它们正交。

反演是保角的，所以关于 \(c_a\) 反演后，它们能保持不变，但上面的点发生了交换，我们作这样的反演，看到 \(K\) 对应了 \(AK\) 延长后与 \(c_b\) 的交点 \(K'\) ， \(L'\) 同理。

注意 \(c_a,c_b\) 的根轴是 \(CD\) ，所以 \(X\) 在根轴上，回忆根心定理的逆定理，我们有 \(KLK'L'\) 共圆 \(c\) 。

反演给出 \(AK\cdot AK'=AL^2\) ，所以 \(AL\) 是切线，同理 \(AL',BK,BK'\) 都是。

这里需要的观察是，圆心 \(O\) 在 \(CD\) 上。因为上面的切线关系说明了 \(O\) 是过 \(A\) 作 \(BL\) 垂线和过 \(B\) 作 \(AK\) 垂线的交点，所以 \(O\) 是 \(\triangle AXB\) 的垂心，自然在 \(XD\) 上。

而 \(LL',KK'\) 对应的极点是 \(A,B\) ，所以过 \(O\) 作 \(AB\) 的垂线交出的点 \(D\) 就是密克点（回忆圆内接四边形密克点的性质），然后 \(T\) 在 \((KLD)\) 上也在 \(l_X=AB\) （ \(X\) 的极线）上，所以必定是 \(KL'\cap K'L\)

我们想要证的是一个角平分线，在这样的情况下，阿氏圆感觉上是最有可能的（当然是指在纯几何范畴内）的方法了。不错的是 \(KL'K'L\) 是调和的，因为 \(BLL'\) 共线， \(B\) 是 \(KK'\) 的极点，我们用透视

现在看到 \((S,T;A,B)=-1\) （以 \(L\) 为透视中心，注意 \(S\) 在 \(AB\) 上是由 \(Brocard\) 定理给出的），我们只要证 \(\angle SCT=Rt\angle\)

回忆若 \(P,Q\) 关于 \(\omega\) 共轭，那么以 \(PQ\) 为直径的圆与 \(\omega\) 正交。这里 \(S,T\) 与 \(A,B\) 根据 \(Brocard\) 定理共轭，所以 \(\odot O\) 与 \(AB,ST\) 为直径的圆正交

现在 \(O\) 在两圆根轴上，两圆根轴垂直于连心线 \(ABST\) ，所以 \(C\) 在根轴上，而 \(C\) 在以 \(AB\) 为直径的圆上，所以也在 \(ST\) 为直径的圆上（这个考虑根轴的方法在我的方法总结笔记里还用过，不常见但是需要考虑）

这就证毕。