圆幂与根轴

等差幂线

\(AB\perp CD\iff AC^2-AD^2=BC^2-BD^2\)

圆幂

定义一个点关于 \(\odot O\) 的圆幂 \(\rho_o(A)=OA^2-R^2\) ：

若 \(A\) 在圆外， \(APQ\) 是 \(\odot O\) 的割线，则 \(AP\cdot AQ=\rho_o(A)\) （ \(P,Q\) 重合即切线）

若 \(A\) 在圆内， \(PAQ\) 是 \(\odot O\) 的弦，则 \(AP\cdot AQ=-\rho_o(A)\)

特别地，对于点圆的幂即 \(\rho_O(A)=OA^2\)

切割线定理经常会与射影定理有一些联系，看到比较多的直角时（包括切线携带的），可以尝试使用射影定理，给出一些共圆与切线。

根轴

两圆的根轴定义为满足 \(\rho_{O_1}(A)=\rho_{O_2}(A)\) 的点 \(A\) 的集合，连心线垂直于根轴

特别地，当两圆相交，两圆交点连线在根轴上，并被连心线垂直平分

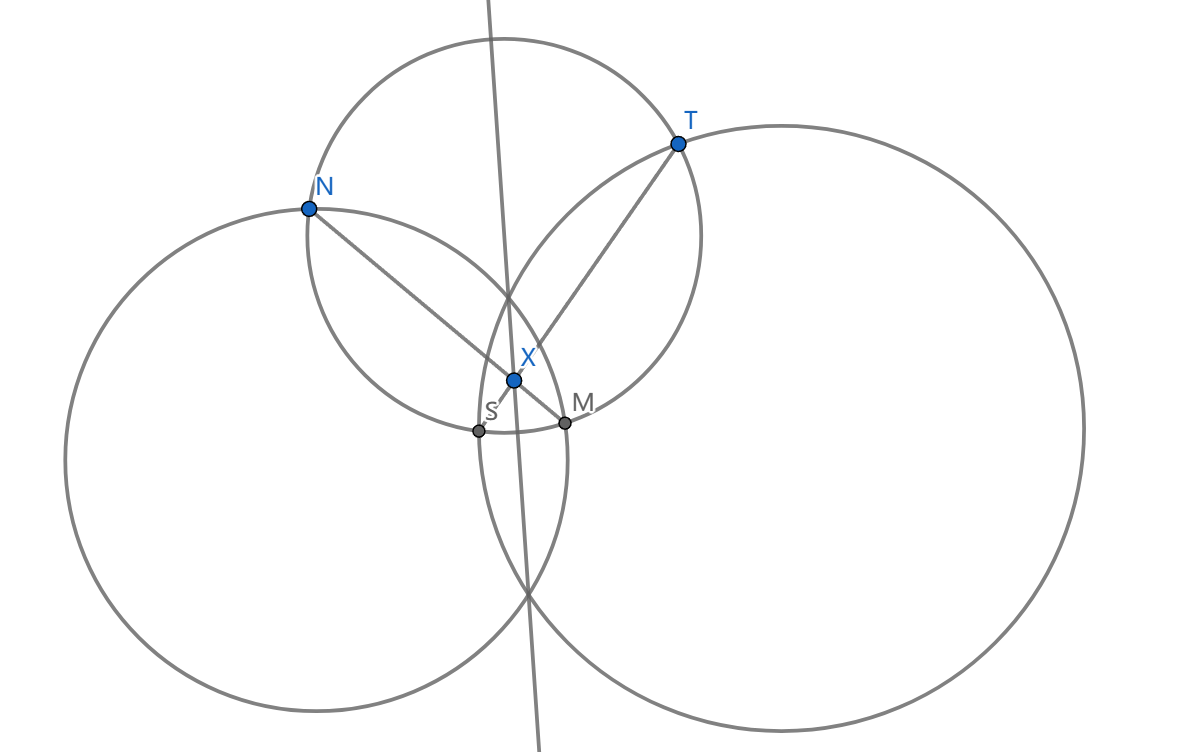
根心定理：三圆两两根轴要么平行，要么交于一点。（直接利用根轴的定义，等式的传递性）

逆定理：如图，若 \(MN\cap ST\) 在 \(\odot O_1,\odot O_2\) 的根轴上，那么这四点共圆。（导圆幂即可）

例1

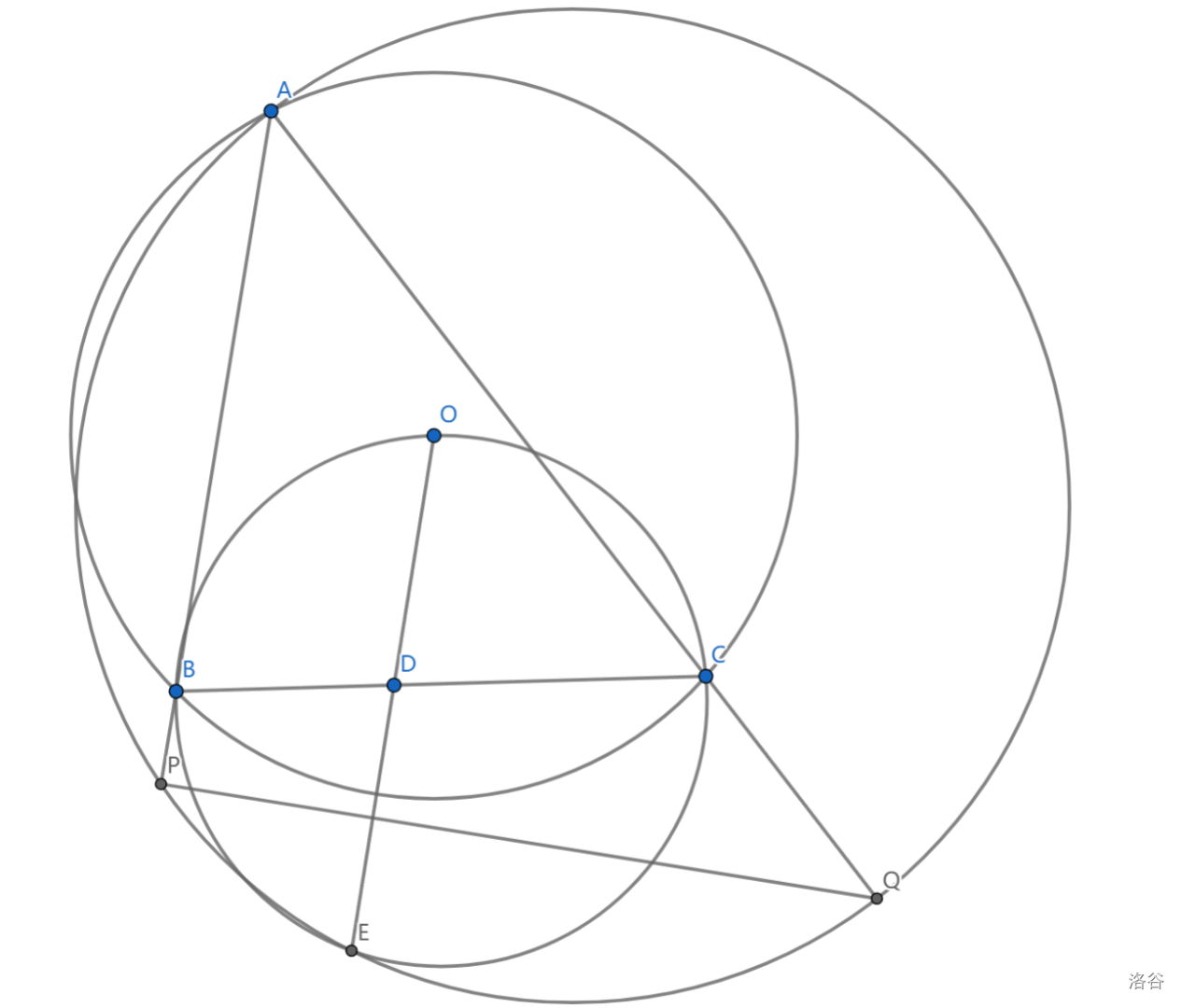
如图， \(\triangle ABC\) 内接于 \(\odot O\) ， \(D\) 是 \(BC\) 上任一点， \(ODE\) 是 \(\odot (OBC)\) 一条弦，\(P,Q\) 是 \(DE\) 中垂线与 \(AB,AC\) 的交点，求证： \(APEQ\) 共圆

这里我们以圆幂，割线的视角来看这个问题

\(\rho_O(P)=PB\cdot PA=OP^2-OB^2\)

由于 \(PD=PE\) ，将 \(D,E\) 视作 \(\odot P\) 上的点，有 \(\rho_P(O)=OD\cdot OE=OP^2-PD^2\)

这里我们要注意一个弧中点（ \(O\) 为 \(BC\) 中点）的常用结论：\(OD\cdot OE=OB^2\)

综上可以得到 \(PD^2=PB\cdot PA\) ，即 \(\triangle PDB\sim \triangle PAD\)

同理 \(\triangle QDC\sim\triangle QAD\)

\(\angle PDB+\angle QDC=\angle PAD+\angle QAD=\angle A\) ，从而 \(\pi-\angle A=\angle PED\) ，即证

例2

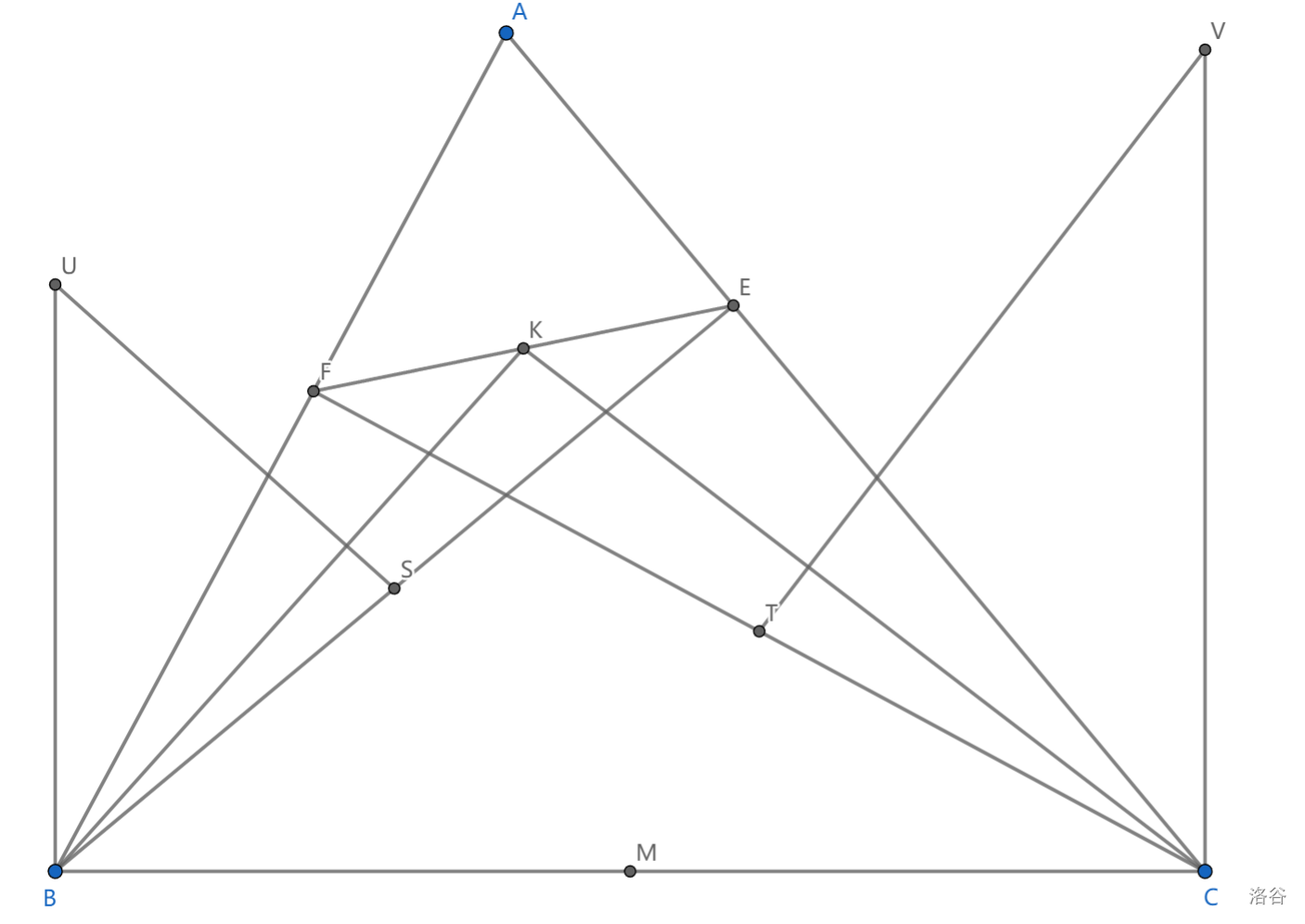
如图，锐角 \(\triangle ABC\) 中， \(BE,CF\) 是两条高， \(K,S,T\) 分别是 \(EF,BE,CF\) 的中点，过 \(S\) 作 \(BK\) 的垂线与过 \(B\) 垂直 \(BC\) 的直线交于点 \(U\) ，过 \(T\) 作 \(CK\) 的垂线与过 \(C\) 垂直于 \(BC\) 的垂线交于点 \(V\) ，求证： \(UV//EF\)

我们取 \(BC\) 中点 \(M\) ，则 \(MK\perp EF\) ，下证明 \(KM\perp UV\)

根据 \(US\perp BK\) ，有 \(BU^2-KU^2=BS^2-KS^2=\frac14 (BE^2-BF^2)\)

根据勾股定理，有 \(UM^2=\frac14BC^2+BU^2\)

两式结合可知 \(UM^2-UK^2=\frac14(BC^2+BE^2-BF^2)\)

同理 \(VM^2-VK^2=\frac14(BC^2+CF^2-CE^2)\)

显然 \(BE^2+CE^2=BF^2+CF^2\) ，即证

例3

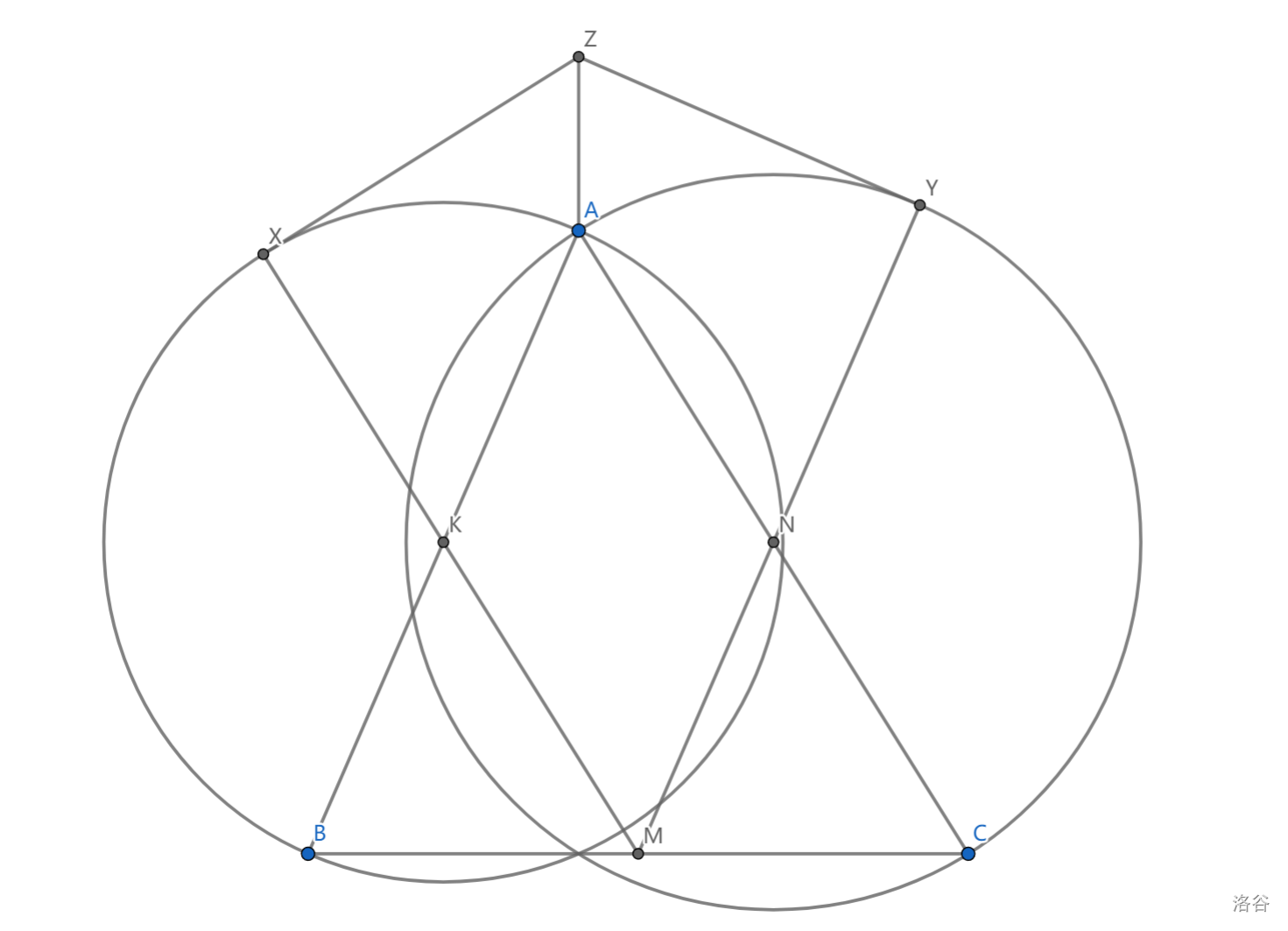
如图， \(\triangle ABC\) 三边中点分别为 \(M,N,K\) ，以 \(AB,AC\) 为直径的圆分别与 \(MK,MN\) 交于点 \(X,Y\) ，过 \(X,Y\) 分别作两圆切线交于 \(Z\) ，求证 \(AZ\perp BC\)

只需注意到两圆另一交点即 \(A\) 在 \(BC\) 上投影，只需证 \(Z\) 在根轴上

即证 \(ZX=ZY\) ，即证 \(MX=MY\) ，实际上 \(MX=MK+XK=\frac12 AC+\frac12 AB=NY+NM=MY\)

例4

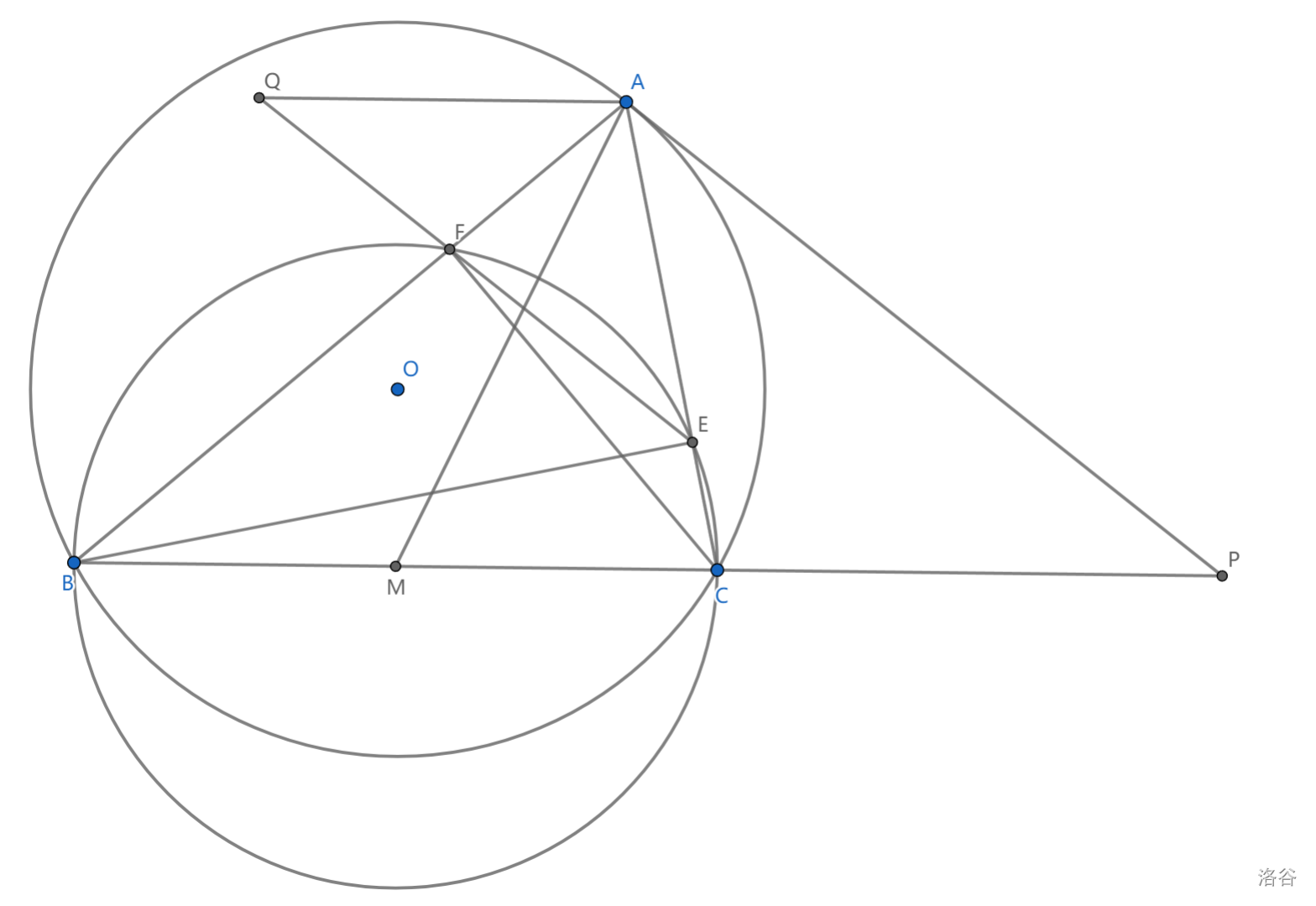
如图，锐角三角形 \(ABC\) 满足 \(AB>AC\) ， \(BE,CF\) 是两条高，\(EF\) 与过 \(A\) 且平行于 \(BC\) 的直线交于 \(Q\) ，过 \(A\) 作 \(\triangle ABC\) 外接圆切线与 \(BC\) 延长线交于点 \(P\) ，\(M\) 为 \(BC\) 中点，求证 \(AM\perp PQ\)

这里注意到 \(PA^2=PC\cdot PB\) ，也就是说 \(P\) 到点圆 \(A\) 和 \(\odot (BCEF)\) 的圆幂是相等的，我们希望证明 \(Q\) 到两圆的圆幂也相等

\(\iff QA^2=QF\cdot QE\)

实际上由 \(AQ//BC\) 可知 \(\angle QAF=\angle ABC=\angle AEQ\) ，从而 \(\triangle AQF\sim \triangle EAQ\) ，即证

例5

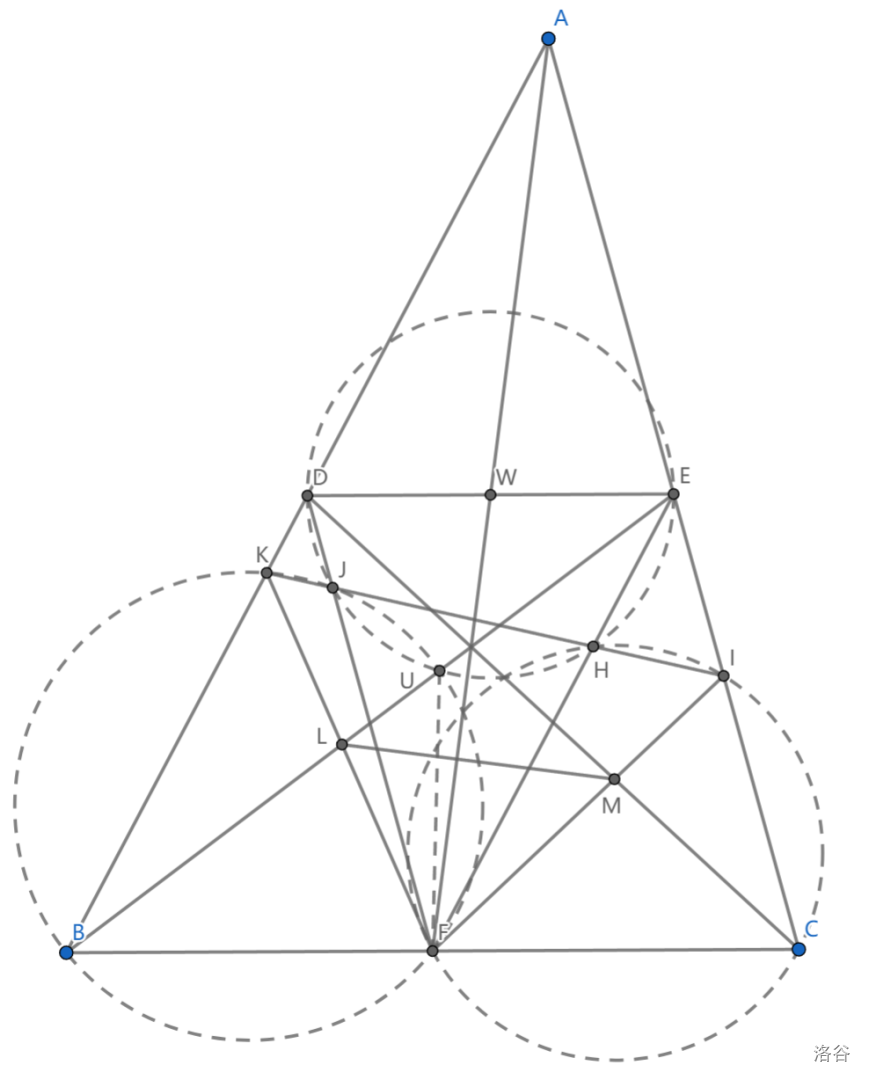
如图， \(\triangle DEF\) 是中点三角形， \(J,H\) 是 \(DF,EF\) 上的垂足， \(JH\) 与 \(AB,AC\) 交于 \(K,I\) ， \(BE\cap KF=L,CD\cap FI=M\) ，求证： \(AF\perp LM\)

首先，由 \(\angle KJF=\angle DJH,\angle KBF=\angle DEF\) ，可知 \(\angle KJF+\angle KBF=\pi\) ， \(KJFB\) 共圆

由 \(DE//BF,DF\) 过两圆交点 \(J\) ，可知两圆另一交点在 \(BE\) 上（ \(Reim\) 引理 ）

又 \(\angle LUF=\angle BUF=\angle BKF=\angle EFK=\angle EFL\) ，知 \(\triangle LUF\sim\triangle LEF\) ，即 \(LU\cdot LE=LF^2\) ， \(L\) 关于点圆 \(F\) 及 \(\odot(DJHF)\) 的幂相等， 同理 \(M\) 相等，即证

例6

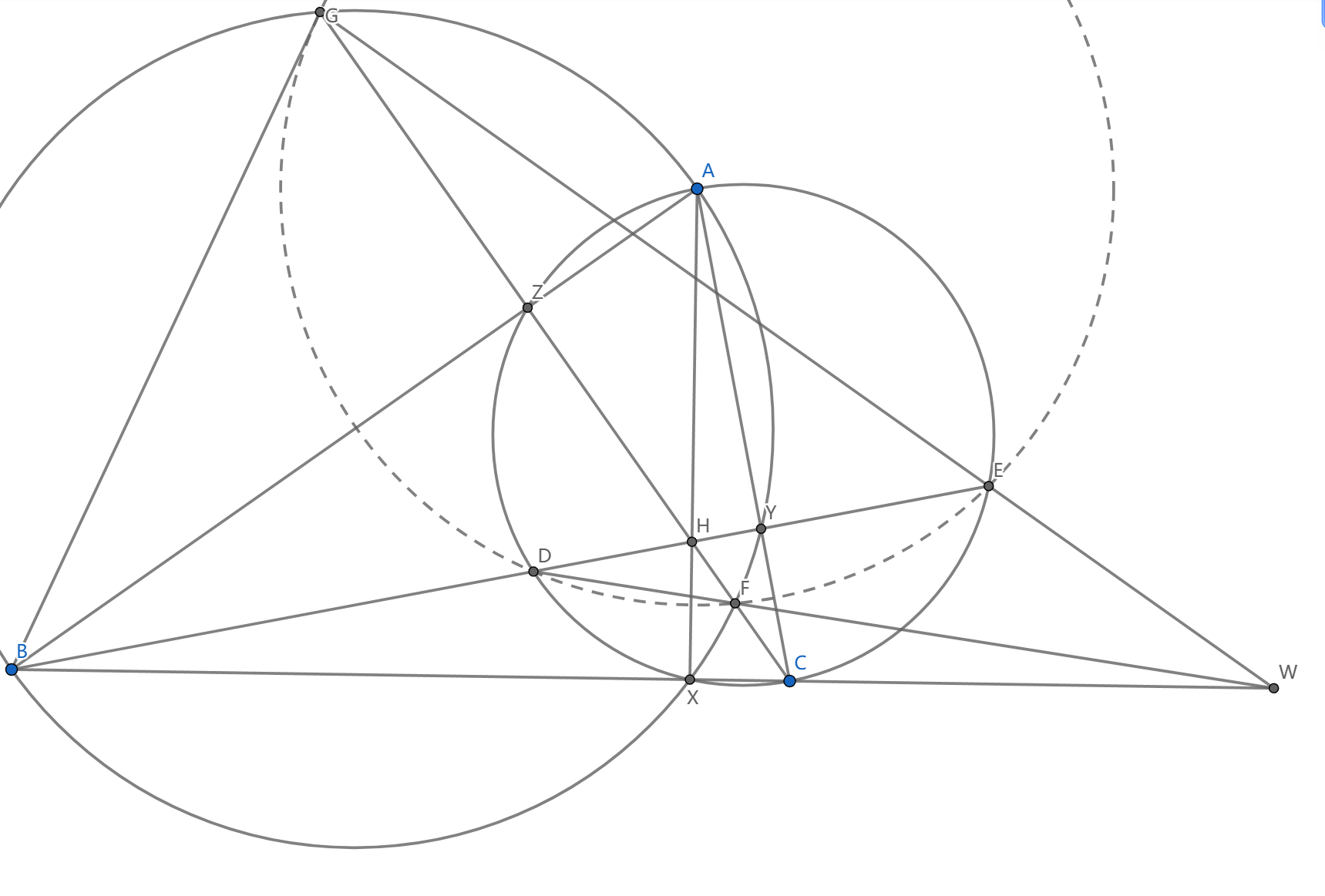
如图， \(\triangle ABC\) 的垂心为 \(H\) ， \(BY,CZ\) 为高， \(BY\) 交 \(AC\) 为直径的圆于 \(D,E\) ， \(CZ\) 交 \(AB\) 为直径的圆于 \(F,G\) ，求证： \(GE,DF,BC\) 交于一点

我们首先看到两圆的根轴即 \(AX\) ，而 \(DE,GF\) 两条弦交于点 \(H\) 在根轴上，这就是我们开始提到的构型，从而 \(DGEF\) 共圆

我们看 \(B\) 的幂，得到了 \(BD\cdot BE=BZ\cdot BA\) ，而以 \(BA\) 的直径的圆中有 $\angle AGB=Rt\angle $ ，以及 \(CG\perp AB\) ，所以用射影定理，有 \(BZ\cdot BA=BG^2\) ，那么 \(BG\) 就是 \(DFEG\) 的切线。

同理 \(BF,CD,CE\) 都是切线。我们看到 \(B\) 的极线是 \(GF\) ， \(C\) 的极线是 \(DE\) ， \(H=GF\cap DE\) ，根据极线的共轭性质，我们看到 \(H\) 的极线是 \(BC\)

而根据 \(Brocard\) 定理， \(H=DE\cap FG\) 的极线是 \(GD\cap EF,GE\cap DF\) 的连线，所以 \(GE\cap DF\) 在 \(BC\) 上，证毕。

下面我们将展示一些进阶的构型。（友情提示：考的概率并不大）

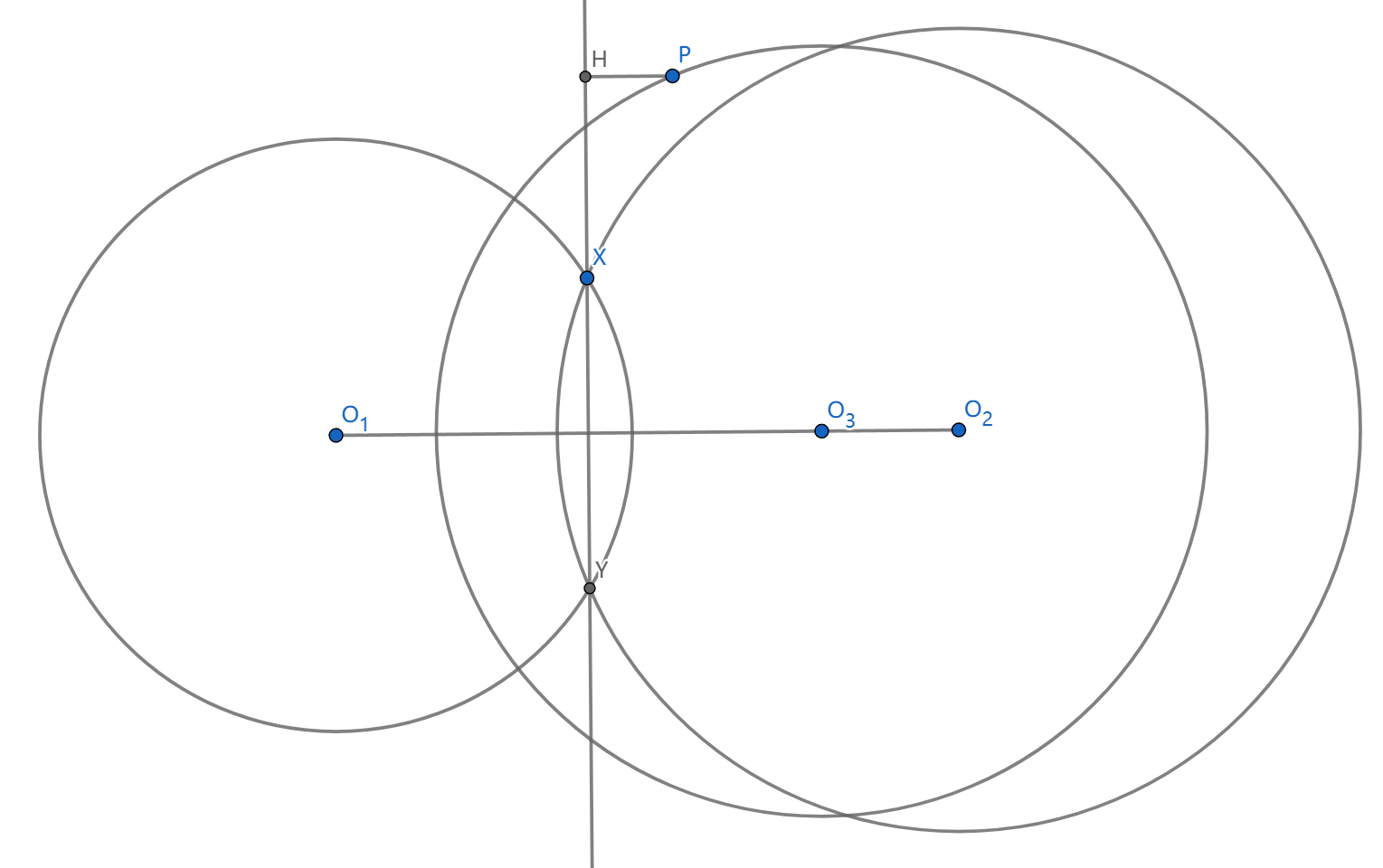
如图，若 \(l\) 是 \(\odot O_1,\odot O_2\) 的根轴， \(P\) 到 \(l\) 的投影是 \(H\) ，则有

\(\rho_{\odot O_1}(p)-\rho{\odot O_2}(p)=2\overline{PH}\cdot O_1O_2\)

这个引理非常容易计算证明，它给出了下面两个命题：

1. 三圆 \(\odot O_1,\odot O_2,\odot O_3\) 共轴的充要条件是 \(\odot O_3\) 上两点 \(P,Q\) 满足 \(\rho_{\odot O_1}(P)/rho_{\odot O_2}(P)=\rho_{\odot O_1}(Q)/rho_{\odot O_2}(Q)\)

2. 三点共线的充要条件是它们关于两圆幂的差是线性关系。

进一步地我们将介绍 \(Poncelet\) 共轴引理（它实际上是 \(Poncelet\) 闭合定理中用到的引理）：

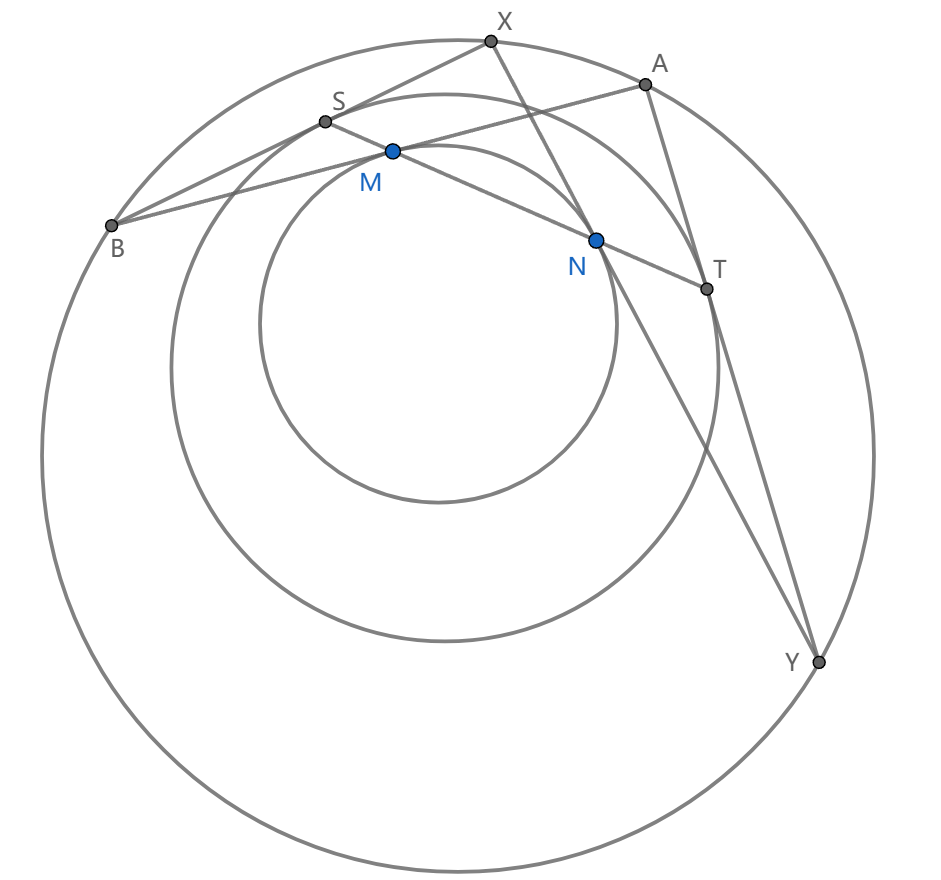
\(AB,XY\) 是圆 \(c_1\) 上的两条弦，与圆 \(c_2\) 切于点 \(M,N\) ，延长 \(MN\) 交 \(BX,AY\) 于 \(S,T\) ，则过 \(S,T\) 与 \(BX,AY\) 相切的圆与 \(c_1,c_2\) 共轴。

这是很容易证明的，只要说明 \(\frac{AT}{AM}=\frac{BS}{BM}\) ，用正弦定理，我们看到只要 \(\angle XST=\angle AST\) ，它们是相等的弦切角。

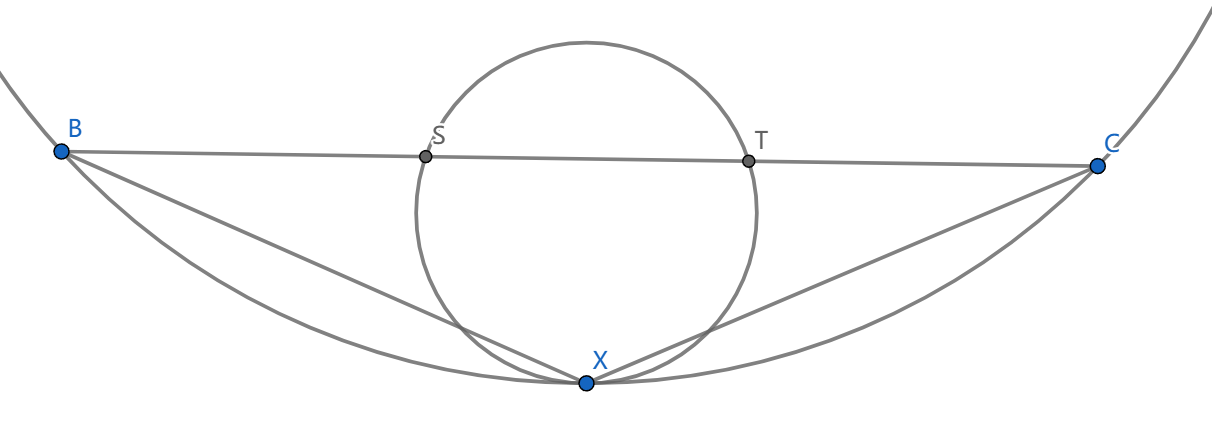
这里还有一个常见的构型，是基于第一个命题的，考虑图中的两个圆和它们的切点 \(X\) （点圆）是共轴的，从 \(BC\) 出发作计算，我们将看到

\(\frac{BX}{CX}=\sqrt\frac{BS\cdot BT}{CS\cdot CT}\)

这意味着，给定点 \(S,T,X\) ，这样的小圆是唯一确定的。

例1

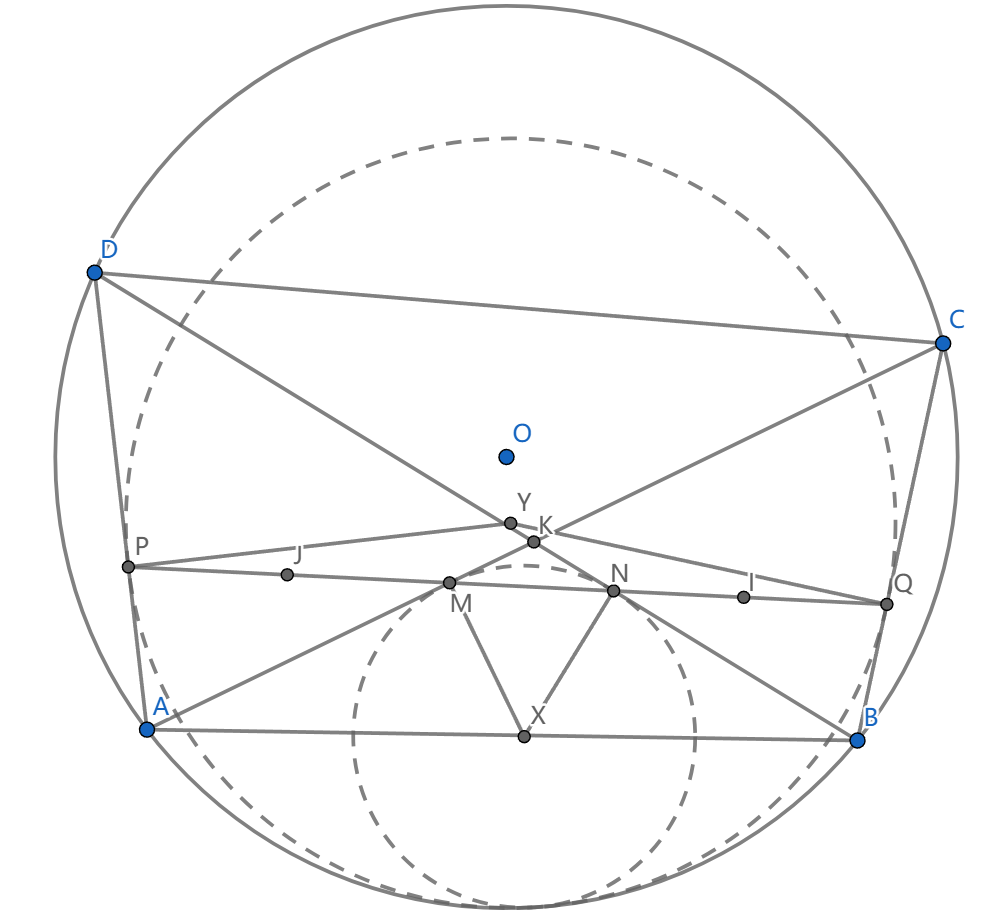
如图，四边形 \(ABCD\) 内接于 \(\odot O\) ， \(I,J\) 为 \(\triangle ABC,ABD\) 的内心，直线 \(IJ\) 分别交 \(AD,AC,BD,BC\) 于 \(P,M,N,Q\) ，过 \(M,N\) 作 \(AC,BD\) 的垂线交于 \(X\) ，过 \(P,Q\) 作 \(AD,BC\) 的垂线交于 \(Y\) ，求证： \(XYO\) 共线

这道题是 \(Poncelet\) 共轴引理的一个直接引用。我们先要给出 \(IJ\) 线的一些性质

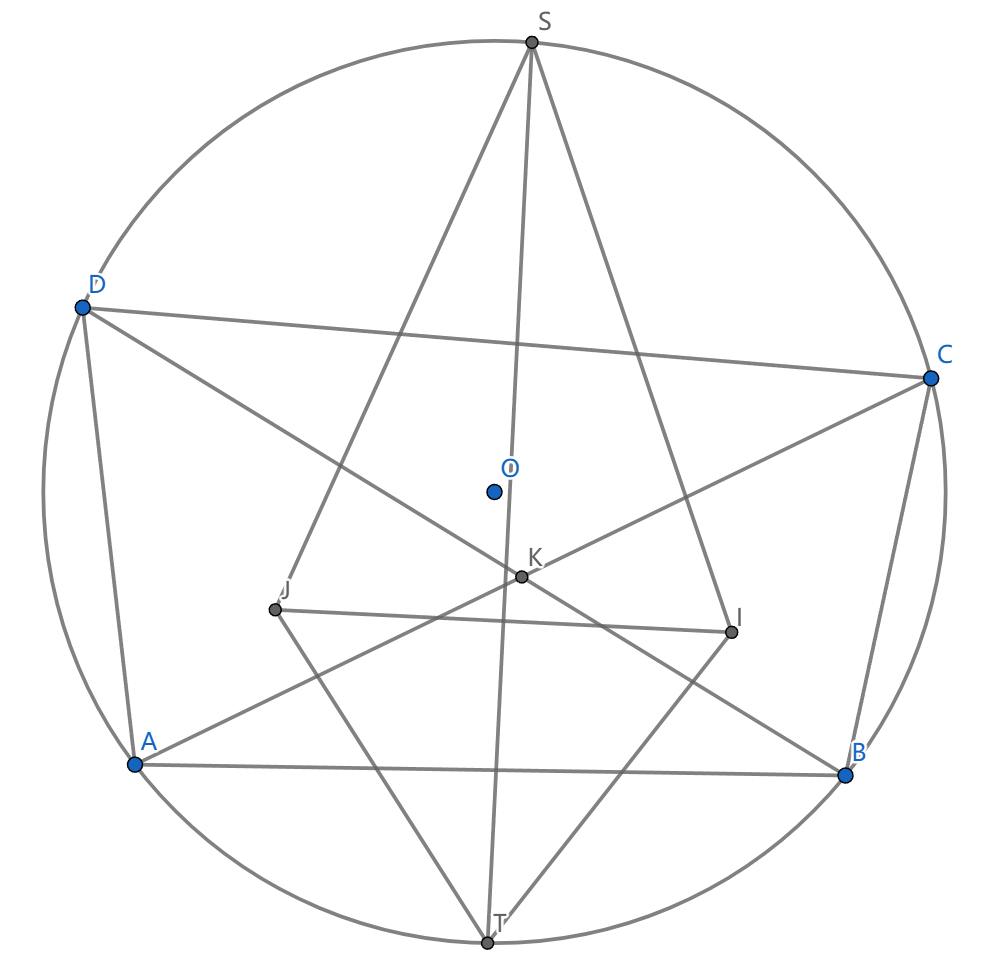
如图，根据鸡爪定理，我们看到 \(SI=SC=SJ,TI=TB=TJ\) ，从而 \(ST\perp IJ\) ，而 \(\angle AKB\) 的平分线平行于 \(ST\) ，从而 \(\angle AKB\) 的平分线垂直 \(MN\) ，所以 \(KM=KN\) ，进而 \(XM=XN\)

并且 \(\angle DAC=\angle DBC\) ，则外角 \(\angle DPQ=\angle CQP\) ，进而 \(YP=YQ\) ，作两个圆，然后用 \(Poncelet\) 共轴引理。

例2

\(\triangle A_1B_1C_1,\triangle A_2B_2C_2\) 拥有相同的垂心与外接圆，垂心为 \(H\) ，外心为 \(O\) ，直线 \(A_1A_2,B_1B_2,C_1C_2\) 围成 \(\triangle PQR\) ，证明： \(\triangle PQR\) 的外心在直线 \(OH\) 上

这两个圆拥有相同的九点圆圆心，我们关于 \(O\) 反演，\(A_1C_1\) 中点变为了 \(A_1C_1\) 关于 \(\odot O\) 的极点（并不是看到九点圆就应当关于 \(H\) 反演的，至少这道题不行）

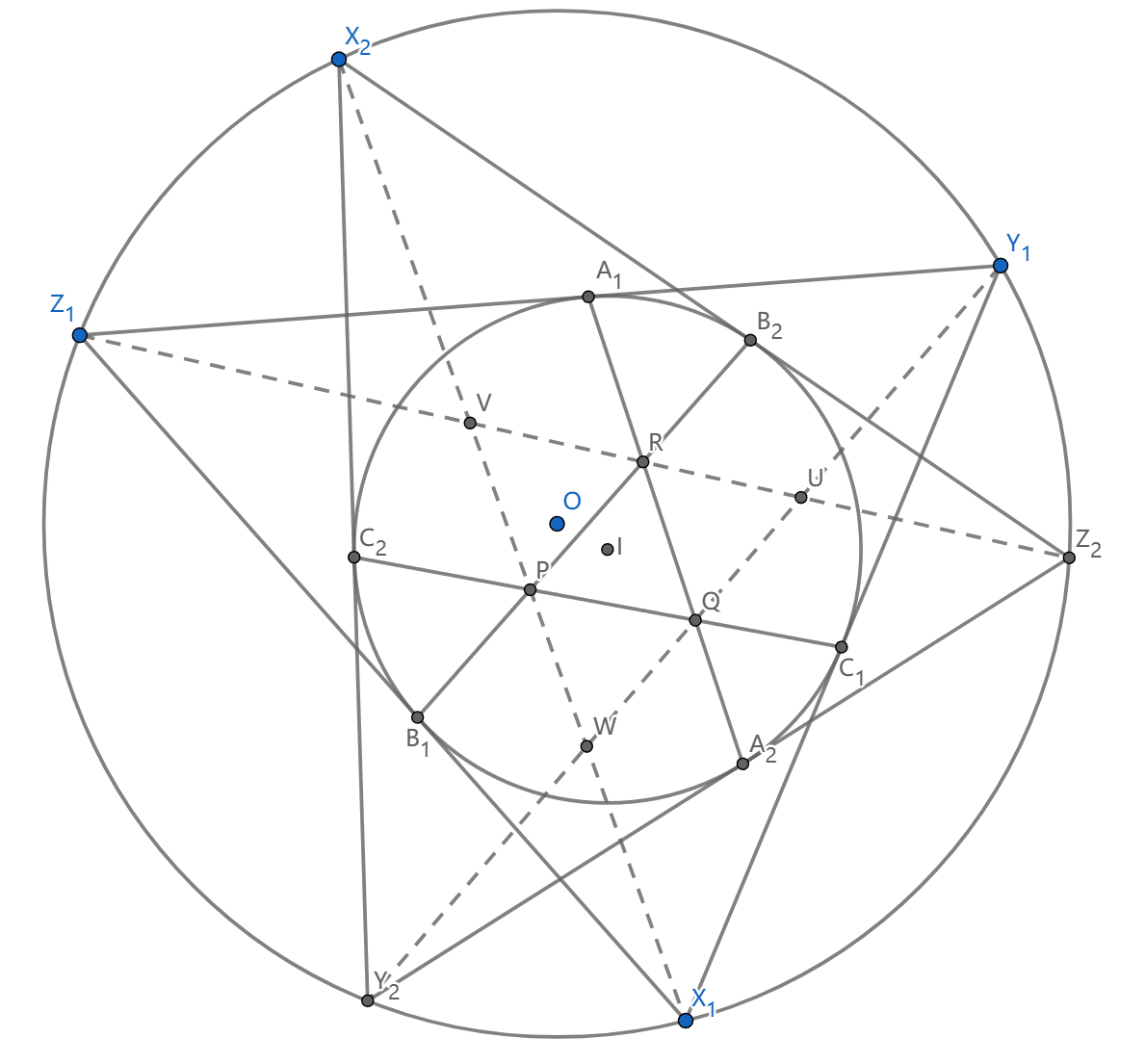
我们设出这些对应的极点构成了 \(\triangle X_1Y_1Z_1,\triangle X_2Y_2Z_2\) ，它们的内切圆与外接圆相同，我们要证的是三圆共轴（因为反演后九点圆圆心依旧在线 \(OH\) 上，尽管它不是大圆的圆心）

我们知道 \(X_1PX_2\) 共线（射影几何(1) 引理 \(9.3\) ），然后设出 \(X_1X_2,Y_1Y_2,Z_1Z_2\) 交出的三角形 \(UVW\) ，希望借助这个三角形完成我们的工作。

我们注意到 \(\angle URQ=\angle A_1RZ_1=\angle Y_1A_1A_2-\angle YZ_1Z_2=\angle Z_2A_2A_1-\angle Z_2Y_2Y_1=\angle UQR\) （用一些简单的弦切角），所以 \(UR=UQ\) ，其它也是同理

这实际上说明了 \(\triangle PQR\) 的外接圆内切于 \(\triangle UVW\)

现在我们准备好计算圆幂比值，我们看

\(\large (\frac{X_1B_1}{X_1P_1})^2=(\frac{\sin \angle X_1PB_1}{\sin \angle X_1B_1P})^2=(\frac{\sin Z_2RB_2}{\sin Z_2B_2R})^2=(\frac{Z_2B_2}{Z_2R})^2\)

这就完成了证明。

例3

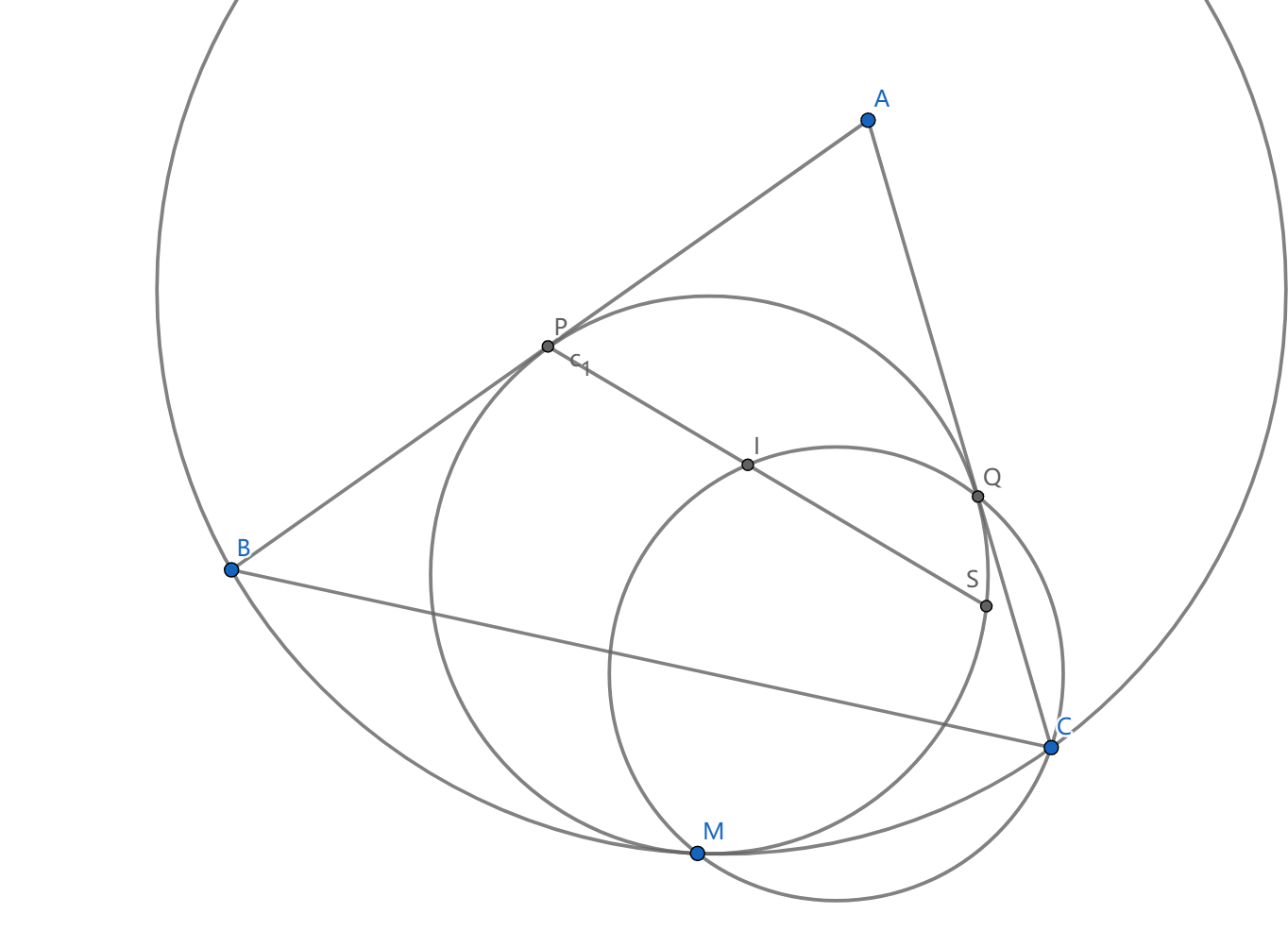
如图， \(I\) 为 \(\triangle ABC\) 的内心，圆 \(c_1\) 与 \(AB,AC\) 切于点 \(P,Q\) ，圆 \(c_2\) 过点 \(B,C\) 并与 \(c_1\) 切于点 \(M\) ，证明： \(PBMI,QCMI\) 分别共圆

我们假设 \(\odot (CQI)\cap \odot(BPI)=M'\) ，我们看到 \(\angle PM'Q=\angle PM'I+\angle QM'I=\angle PBI+\angle QCI=\frac B2+\frac C2=\angle APQ\) ，所以 \(M'\in c_1\)

圆 \(c_2\) 并没什么用处，我们用上面提到的构型尝试消去，我们要证的是

\(\frac{BM'}{CM'}=\frac{BP}{CQ}\) （右边就是 \(B,C\) 到这个圆的幂）

我们设出了 \(M'\) 是两圆交点，对这个性质还没有利用完全。我们得找一些旋转相似（这里 \(Reim\) 不是很现实）已经知道了 \(M'\in c_1\) ，所以可以看到 \(\triangle BP'M\sin \triangle ISM'\)

类似构造点 \(T\) ，因为 \(P,Q\) 关于 \(AI\) 对称，所以 \(S,T\) 也会关于 \(AI\) 对称，从而 \(IS=IT\)

而两组相似给出了 \(\frac{BP}{BM'}=\frac{IS}{IM'},\frac{CP}{CM'}=\frac{IT}{IM'}\) ，这就证毕。

例4

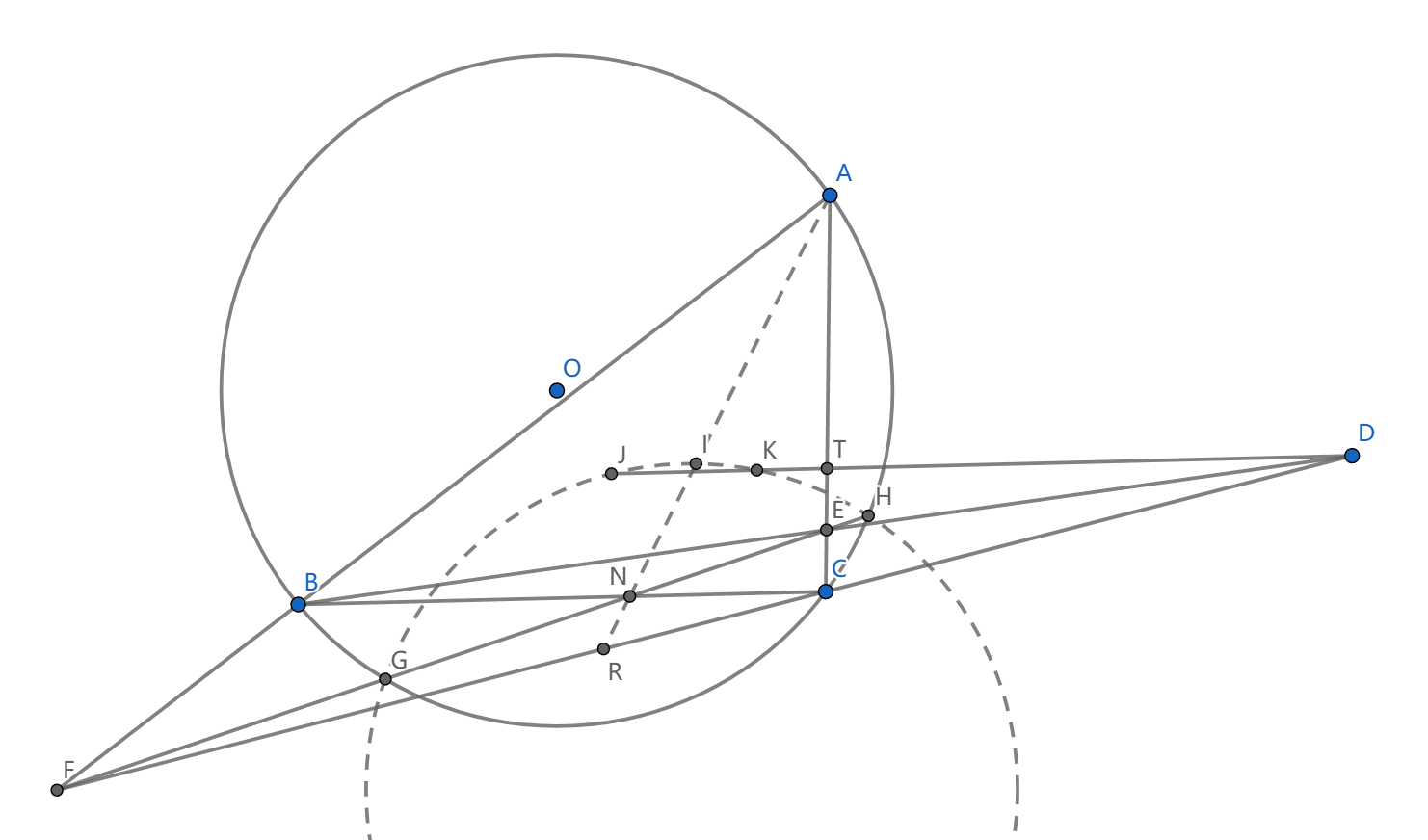
如图， \(\triangle ABC\) 内接于圆 \(\omega\) ， \(I\) 为内心， \(D\) 在 \(\angle BAC\) 的外角平分线（ \(D\) 在 \(\omega\) 外）， \(E=AC\cap BD,F=AB\cap CD\) ，直线 \(EF\) 与 \(\omega\) 交于 \(G,H\) 两点，过 \(D\) 作 \(BC\) 的平行线交 \(\triangle IGH\) 于 \(J,K\) ，求证： \(J,K\) 是 \(\triangle ABC\) 的等角共轭点。

我们先说，如果 \(J,K\) 是等角共轭点并且 \(JK//BC\) ，设 \(JK\cap AC=T\) ，我们看到 \(CJ,CK\) 是等角线等价于 \(\angle TCK=\angle TJC\) 即 \(TK\cdot TJ=TC^2\) ，我们只要证明 \(T\) 到 \(\odot (IGH)\) 的幂是 \(TC^2\)

点 \(T\) 的幂是根本没有办法计算的。我们会使用线性幂差，我们计算 \(A,E\) 到两圆的幂差， \(\frac{AT}{TE}\) 作为替代。

定义 \(f(X)=\rho_{\odot(GIH)}(X)-\rho_{\odot(BAC)}(X)\)

首先 \(E\) 在根轴 \(GH\) 上，所以 \(f(E)=0\)

其次我们看 \(A\) 到 \(\odot(IGH)\) 的幂，我们延长 \(AI\) 交 \(\odot(IGH)\) 交于 \(I_A\) ，看完全四边形 \(BFCE\) ，可以看到 \((F,C;R,D)=-1\) ，而 \(AB,AI,AC,AD\) 恰好是调和线束，这就说明 \(N,R\) 都在 \(AI\) 上

于是 \(IN\cdot I_AN=N\cdot NH=BN\cdot NC\) ，于是 \(IBI_AC\) 共圆，我们知道这个 \(I_A\) 就是旁心（鸡爪圆）

所以 \(f(A)=AI\cdot AI_A=AB\cdot AC\)

我们最后看到 \(f(T)=\frac{TE}{AE}f(A)+\frac{AT}{AE}f(E)=\frac{TE}{AE}\cdot AB\cdot AC\)

我们最后需要证明 \(TE\cdot AB=AE\cdot TC\) ，这是一个简单的构型，实际上 \(\frac{AB}{AE}=\frac{DB}{DE}=\frac{TC}{TE}\)

例5

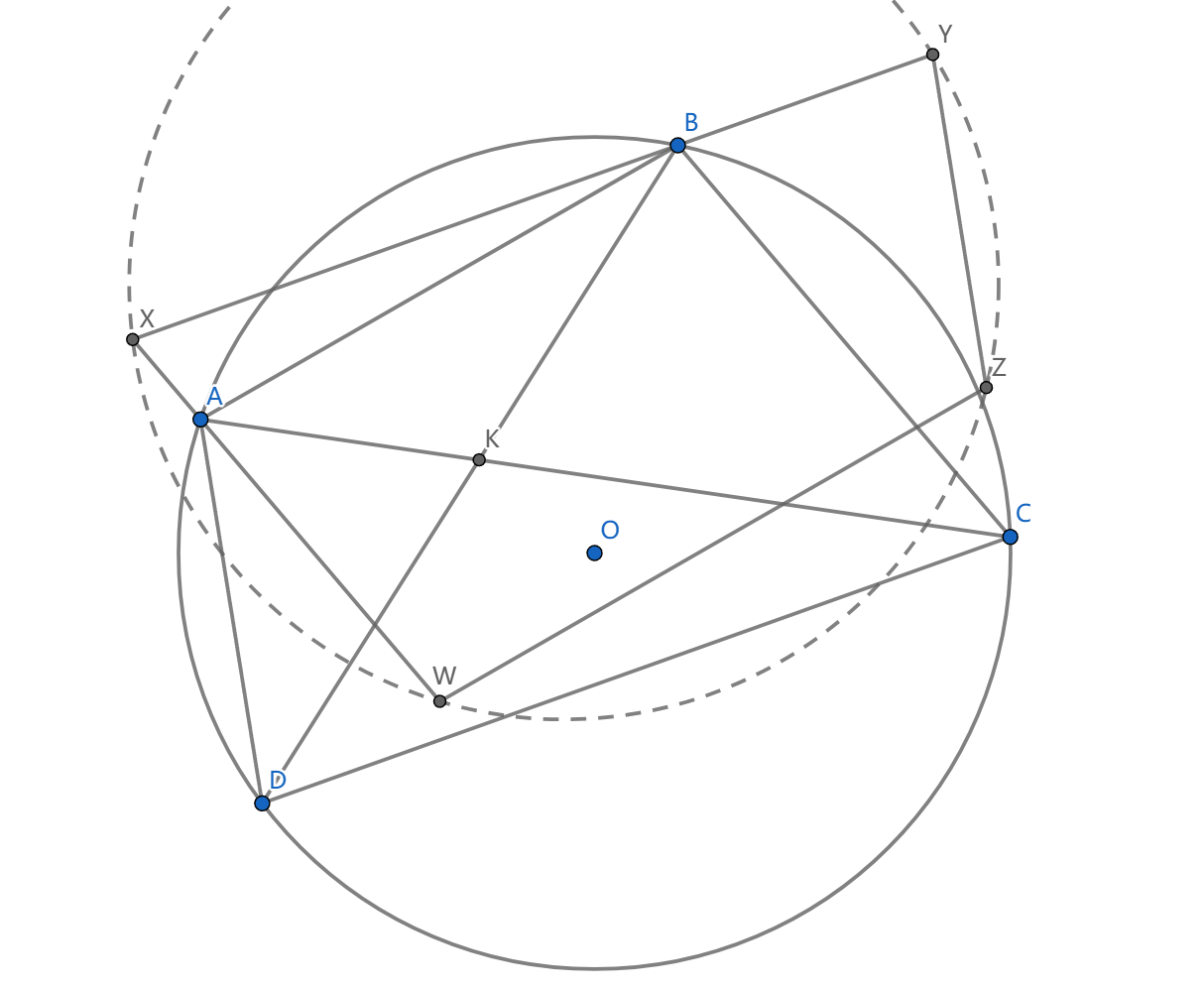
如图， \(ABCD\) 内接于圆 \(\omega\) ，过 \(A\) 作 \(BC\) 的平行线 \(l_a\) ，类似地做四条平行线交出四边形 \(XYZW\) ，内接于圆 \(\omega\) ， \(K=AC\cap BD\) ，求证： \(K\) 在 \(\omega\) 和 \(\gamma\) 的根轴上。

很容易导出 \(XYZW\) 共圆。

这个题目也是比较典型的线性幂差，定义 \(f(P)=\rho_\omega(P)-\rho_\gamma(P)\) ，我们看到 \(f(K)=0\iff \frac{CK}{AC}f(A)+\frac{AK}{AC}f(C)=0\iff \frac{CK}{AC}\cdot XA\cdot AW=\frac{AK}{AC}\cdot CZ\cdot CY\)

\(\large\iff \frac{AX\cdot AW}{CY\cdot CZ}=\frac{AK}{CK}\)

直接用正弦导：

\(\large LHS=\frac{AB\cdot \frac{\sin \angle ABX}{\sin C}\cdot AD\cdot \frac{\sin \angle DAB}{\sin B}}{CB\cdot\frac{\sin \angle DCB}{\sin D}\cdot CD\cdot\frac{\sin \angle CDZ}{\sin A}}=\frac {AK}{CK}\)

其中用到 \(\angle ABX=\angle CDZ\)