等角线与等角共轭点

想了解更多的看纯几何吧4684，这里只是简单介绍

高联如果考等角共轭点的鬼晦性质我直接紫砂了

等角线

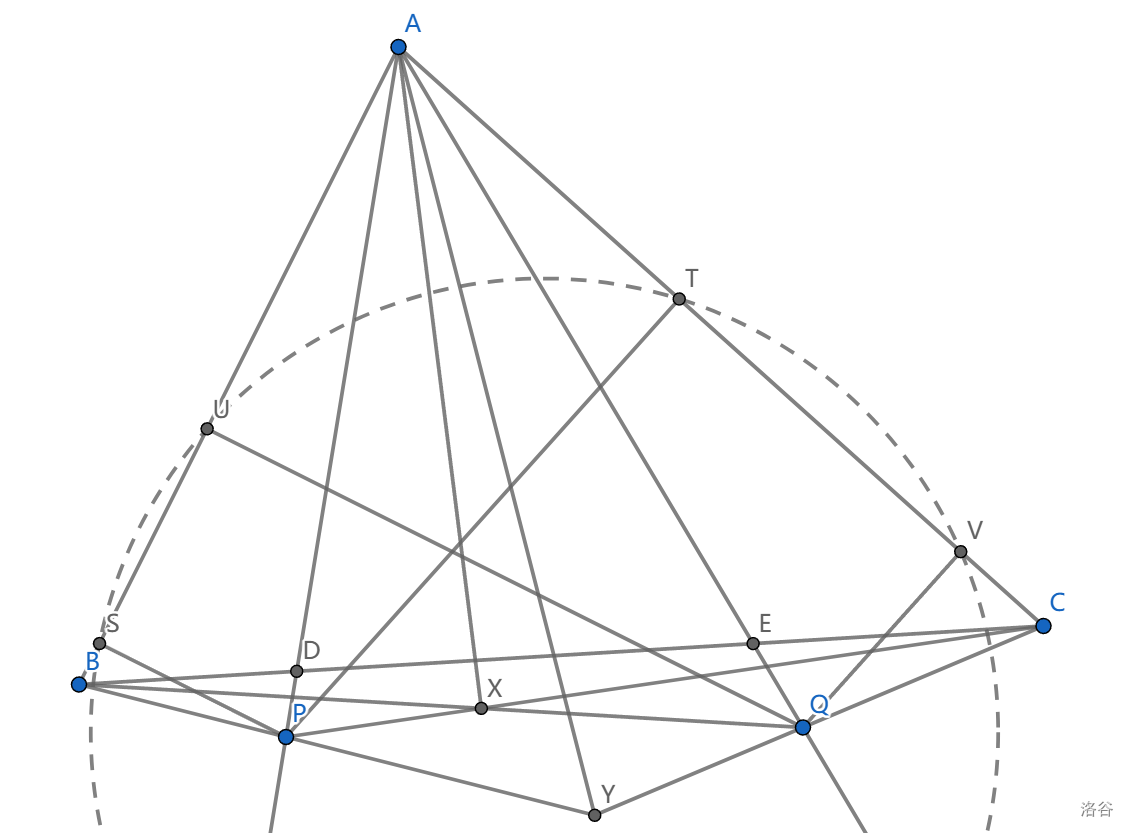
称 \(AP,AQ\) 是关于 \(\angle BAC\) 的等角线，如果 \(\angle PAB=\angle QAC\)

1. （完全四边形中的等角线）设 \(X=BQ\cap CP,Y=BP\cap CQ\) ，则 \(AX,AY\) 是 \(\angle BAC\) 的等角线

这个性质我不建议大家记构型（毕竟是完全四边形），只要意识到三组点中如果两组关于某点形成了等角线结构，那么第三者也是如此。

设 \(X'\) 是 \(BQ\) 上一点，满足 \(AX',AY\) 是等角线，要证 \(CX'P\) 共线，用第二角元梅氏定理：

\(\frac{\sin \angle BAP}{\sin \angle PAY}\cdot \frac{\sin\angle YOQ}{\sin \angle QOC}\cdot \frac{\sin\angle CAX'}{\sin \angle X'AB}=1\)

这个就是完全四边形 \(QYPXCB\) 中的等角线构型。

2. 设 \(P,Q\) 在 \(AB,AC\) 上的投影是 \(S,T,U,V\) ，则 \(STUV\) 共圆，圆心是 \(P,Q\) 中点 （作平行线可以得到四点共二次曲线，不过没啥用）

3. \(AP,AQ\cap BC=D,E\) ，则 \(\frac{BD}{DC}\cdot \frac{BE}{EC}=(\frac{AB}{AC})^2\)

例1

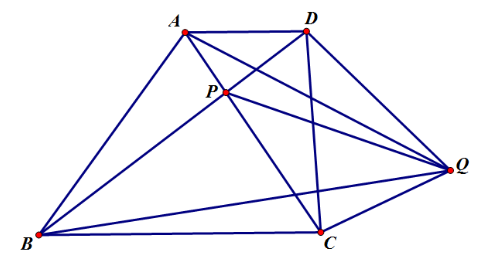
(IMOSL2007)如图，梯形 \(ABCD\) 对角线交于点 \(P\) ，点 \(Q\) 在梯形 \(ABCD\) 外，在直线 \(AD,BC\) 之间，满足 \(\angle AQD=\angle CQB\) ，求证：\(\angle BQP=\angle DAQ\)

设 \(P_\infty=AD\cap BC\) ，根据完全四边形中的等角线，我们看到 \(QP,QP_\infty\) 也是 \(\angle BQA\) 的等角线

而 \(\angle DAQ=\angle AQP_\infty\) ，这就证毕。

例2

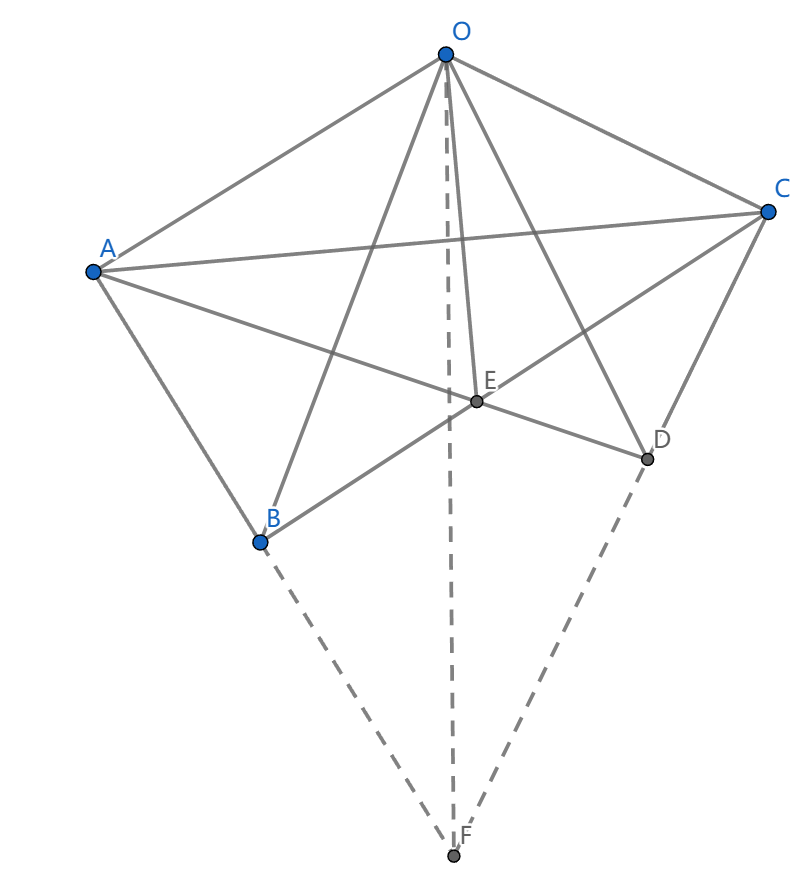
如图， \(\triangle OAB\sim\triangle OCD\) （逆相似）， \(E=AD\cap BC\) ，求证： \(OE\perp AC\)

构造 \(F=AB\cap CD\) ，我们看到 \(OE,OF\) 是 \(\angle AOC\) 的等角线，同时还有 \(OAFC\) 共圆

所以 \(\angle COE=\angle AOF=\angle ACF=Rt\angle -\angle OCA\) ，证毕。

例3

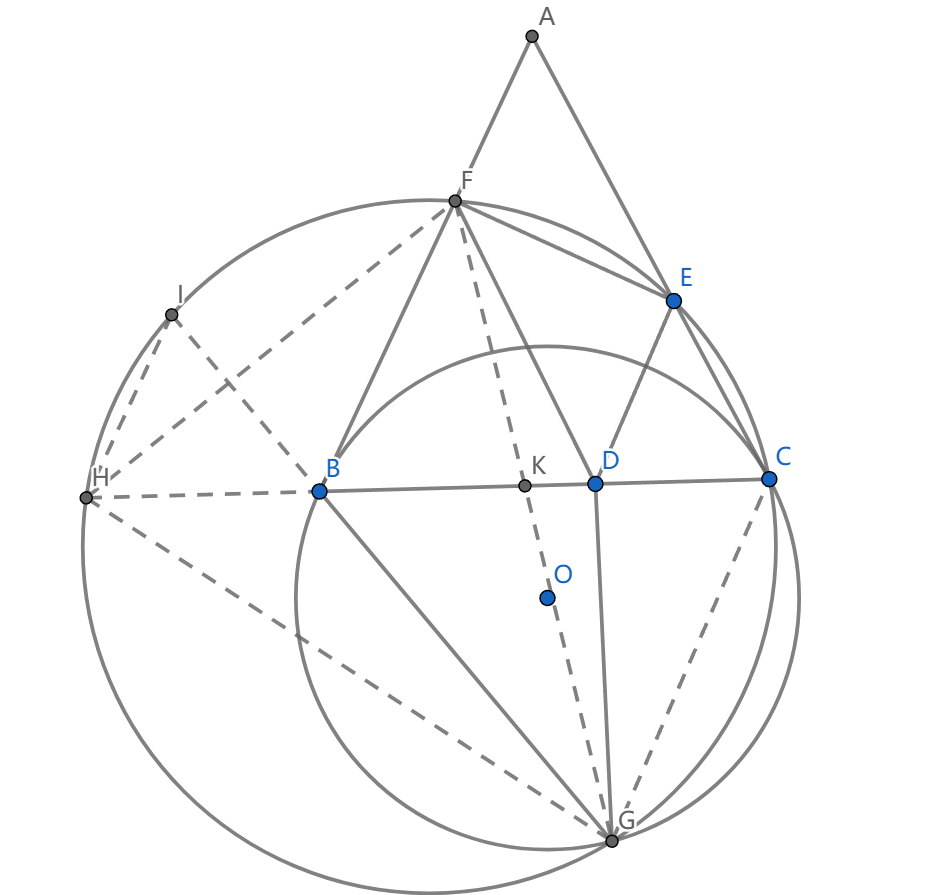
如图，过 \(\odot O\) 上两点 \(B,C\) 作切线交于 \(A\) ， \(D,E,F\) 在 \(BC,AB,AC\) 上，满足 \(\angle BDE=\angle CDF\) ， \(\triangle CEF\) 的外接圆交 \(\odot O\) 于 \(G\) ，求证 \(\angle AEF=\angle BGD\)

我们首先知道 \(\angle AEF=\angle CGF\) ，所以要证明 \(GD,GF\) 是 \(\angle BGC\) 的等角线，设 \(K=GF\cap BC\) ，所以要证 \(\frac{BK}{CK}\cdot \frac{BD}{CD}=(\frac{BG}{CG})^2\)

接下来就很难做了。我们发现圆很难以利用——上面一点圆幂都导不了，两圆相交也没有什么可用的。我们先构造一个点 \(H\) ，这样或许有一组旋转相似，但这样还是处理不好，我们可以延长 \(BG\) ，这样就会有关于 \(B\) 的圆幂，或者说一组相似

旋转相似构型给出了 \(\angle EGC=\angle HGI\) ，从而 \(HI=CE\) ，给出了一个等腰梯形，结合等腰三角形，我们看到 \(HI//BF\)

利用相似，我们有 \(\frac{BD}{CD}=\frac{BF}{CE}=\frac{BF}{HI}\)

我们用正弦定理，看到 \(\frac{BK}{CK}=\frac{BG}{CG}\cdot \frac{\sin\angle BGF}{\sin \angle FHB}=\frac{BG}{CG}\cdot \frac{\sin \angle IHF}{\sin \angle FHB}\)

而 \(\frac{BG}{CG}=\frac{BH}{HI}\) ，综合一下，我们要证：

\(\frac{BG}{CG}\cdot \frac{\sin \angle IHF}{\sin \angle FHB}\cdot \frac{BF}{HI}=\frac{BG}{CG}\cdot \frac{BH}{HI}\)

因为 \(\frac{BF}{\sin \angle FHB}=\frac{BH}{\sin \angle HFI}\) ，这个等式是容易验证的。

等角共轭点

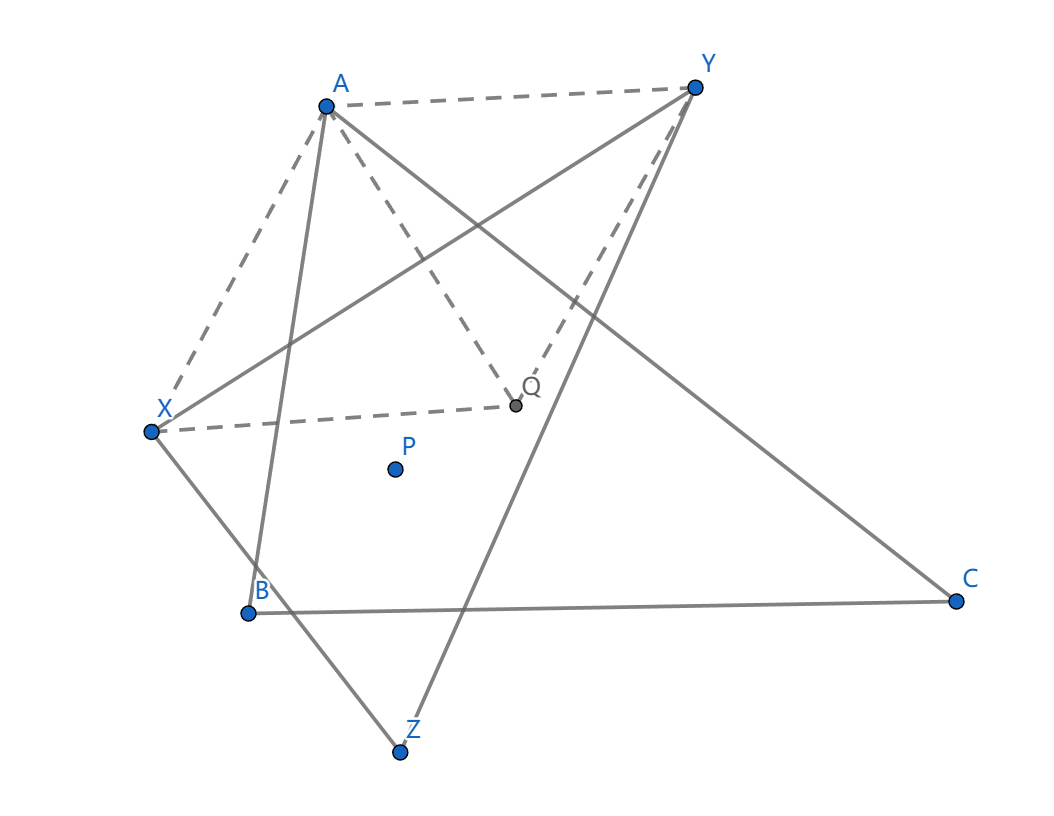
如图，若 \(P,Q\) 满足 \(AP,AQ\) 是 \(\angle BAC\) 的等角线， \(BP,BQ\) 是 \(\angle ABC\) 的等角线， \(CP,CQ\) 是 \(\angle ACB\) 的等角线，则 \(P,Q\) 称为关于 \(\triangle ABC\) 的等角共轭点

1. 只要两组等角线成立，就能推出第三组

2. 点 \(P\) 关于三边的对称点为 \(X,Y,Z\) ，则 \(Q\) 是 \(\triangle XYZ\) 的外心

证明异常的简单，很容易证明 \(\triangle AXQ\cong \triangle AYQ\)

3. \(\angle BPC+\angle BQC=\angle BAC(+\pi)\)

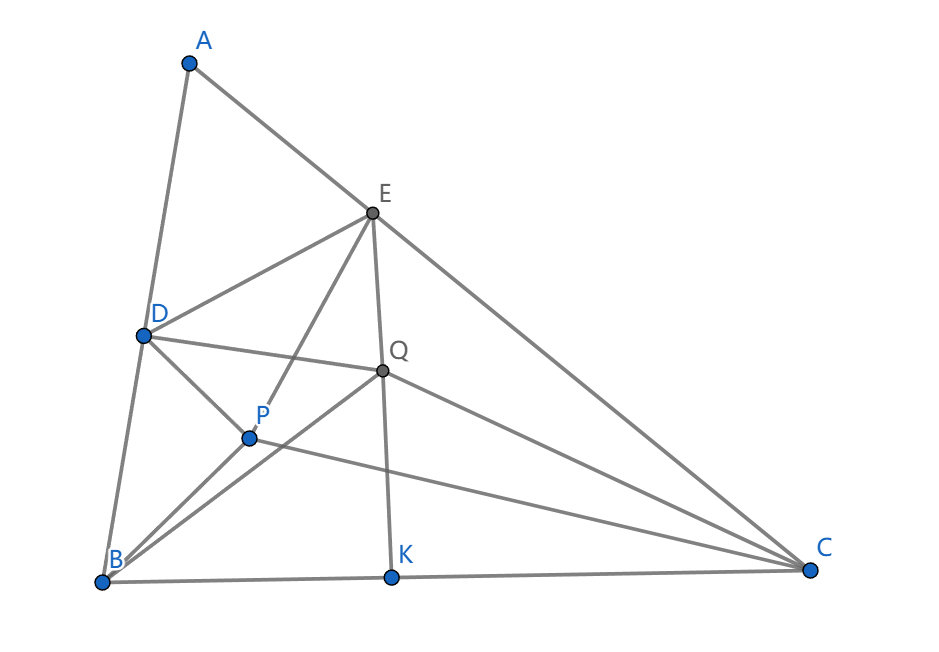
4. \(D,E\) 在边 \(AB,AC\) 上，则 \(\angle DPE=\pi-\angle BPC\iff\angle DQE=\pi-\angle BQC\)

我们知道 \(\angle BDP+\angle CEP=\angle DAE+\angle DPE=\angle BQC\) （根据性质 \(3\) ），于是取 \(BC\) 上点 \(K\) 使得 \(\angle BQK=\angle BDP\) ，则 \(\angle CQK=\angle CEP\)

现在 \(\triangle BQK\sim\triangle BPD,\triangle CQK\sim\triangle CPE\) ，我们看到 \(\angle CQE+\angle BQD=\pi\) ，这就完成了证明。

5. 两个等角共轭点在三边的六个投影共圆（用等角线性质即可）

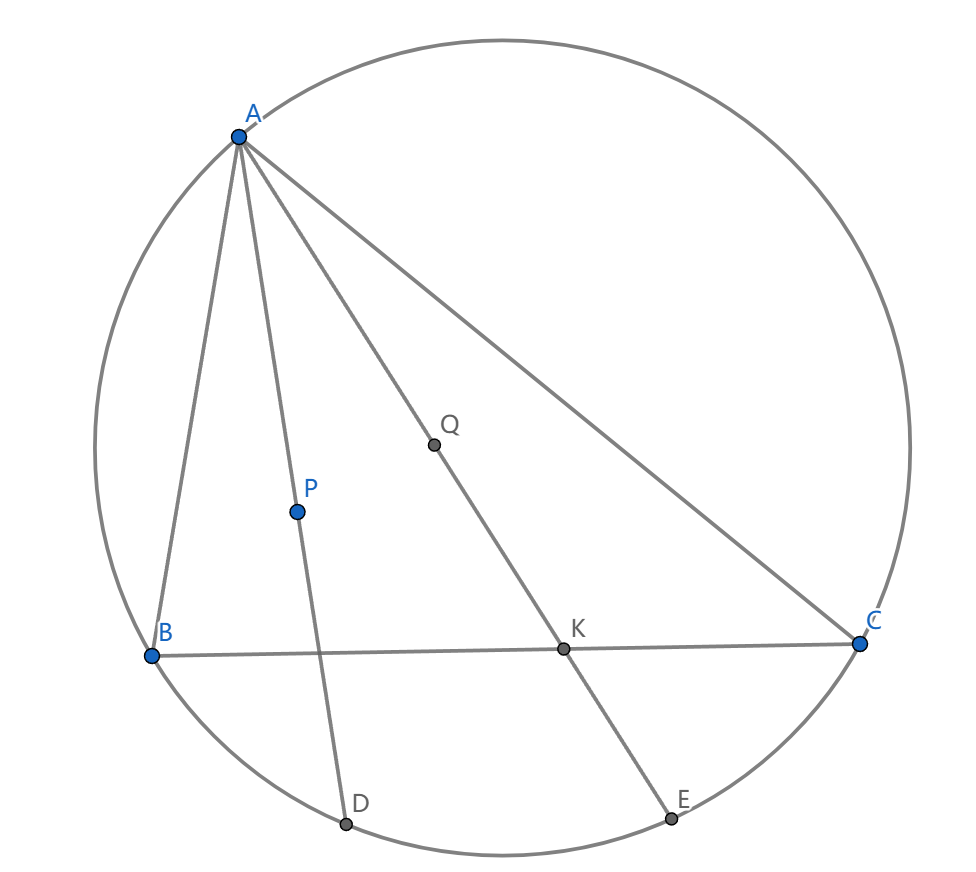
6. \(\frac{AP}{PD}=\frac{QK}{KE}\)

证明 \(\triangle ADC\sim\triangle CEK,\triangle PDC\sim \triangle CEQ\)

注：复数分析等角共轭点是很方便的。

（完全）四边形也有等角共轭点，定义类似，并且两个等角共轭点在四边的投影八点共圆。特别地，四边形中一点 \(P\) 有等角共轭点的充要条件是 \(P\) 在四边上的投影共圆。

另一个更常用的充要条件是 \(\angle APB+\angle CPD=\pi\) ，是上面的推论。

此外，如果 \(P,Q\) 是 \(ABCD\) 的等角共轭点，那么 \(A,C\) 是 \(BPDQ\) 的等角共轭点。（用第二个充要条件导导角）

例1

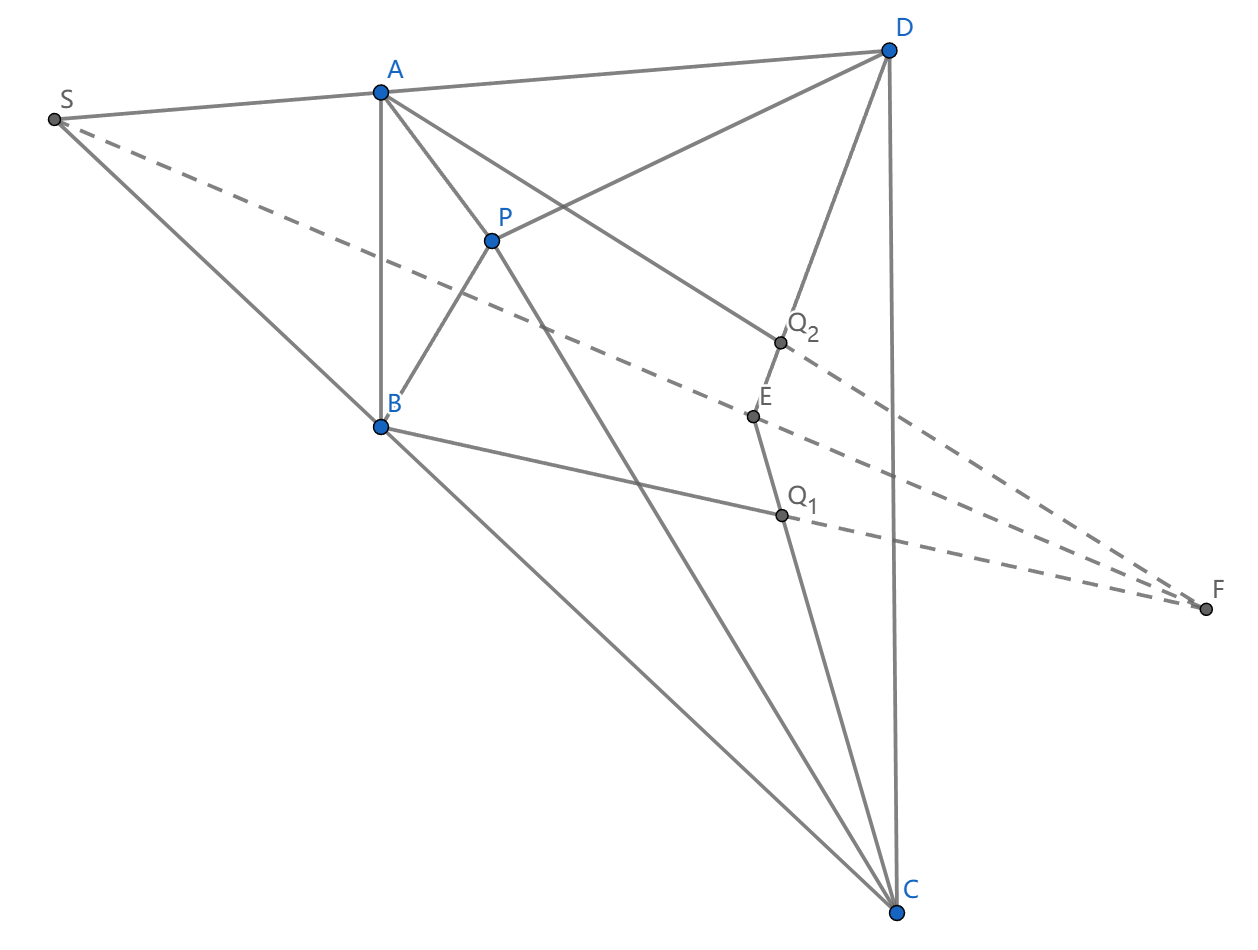
如图，四边形 \(ABCD\) 内有一点 \(P\) ，\(Q_1\) 是 \(BP\) 关于 \(\angle ABC\) 等角线和 \(CP\) 关于 \(\angle BCD\) 等角线的交点，同理定义 \(Q_1\) 。求证： \(Q_1Q_2//AB\iff Q_1Q_2//CD\)

设 \(S=AD\cap BC,E=CQ_1\cap DQ_2,F=AQ_2\cap BQ_1\) ，则 \(P,E\) 是 \(\triangle SCD\) 等角共轭点， \(P,F\) 是 \(\triangle SAB\) 等角共轭点

然后 \(\angle FSB=\angle ESC=\angle DSP\) ，说明 \(FES\) 共线，用笛沙格定理， \(\triangle ADQ_2,\triangle BCQ_1\) 关于直线 \(FES\) 透视等价于 \(Q_1Q_2,AB,CD\) 交于一点，证毕。

注：不用笛沙格定理，直接证明 \(Q_1,Q_2,AB\cap CD\) 共线即可，做法一样

例2

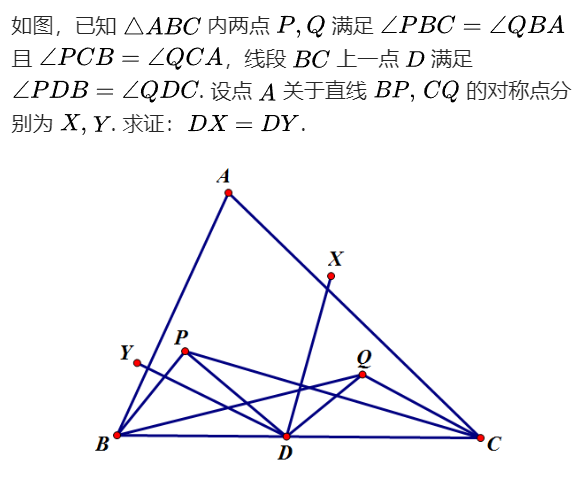
注意到 \(P,Q\) 是四边形 \(ABDC\) 的等角共轭点，然后 \(A,D\) 是四边形 \(BPCQ\) 的等角共轭点，现在 \(A\) 关于该四边形的反射共圆，圆心为 \(D\) 。