射影几何(2)

引理 \(13.1\) ：

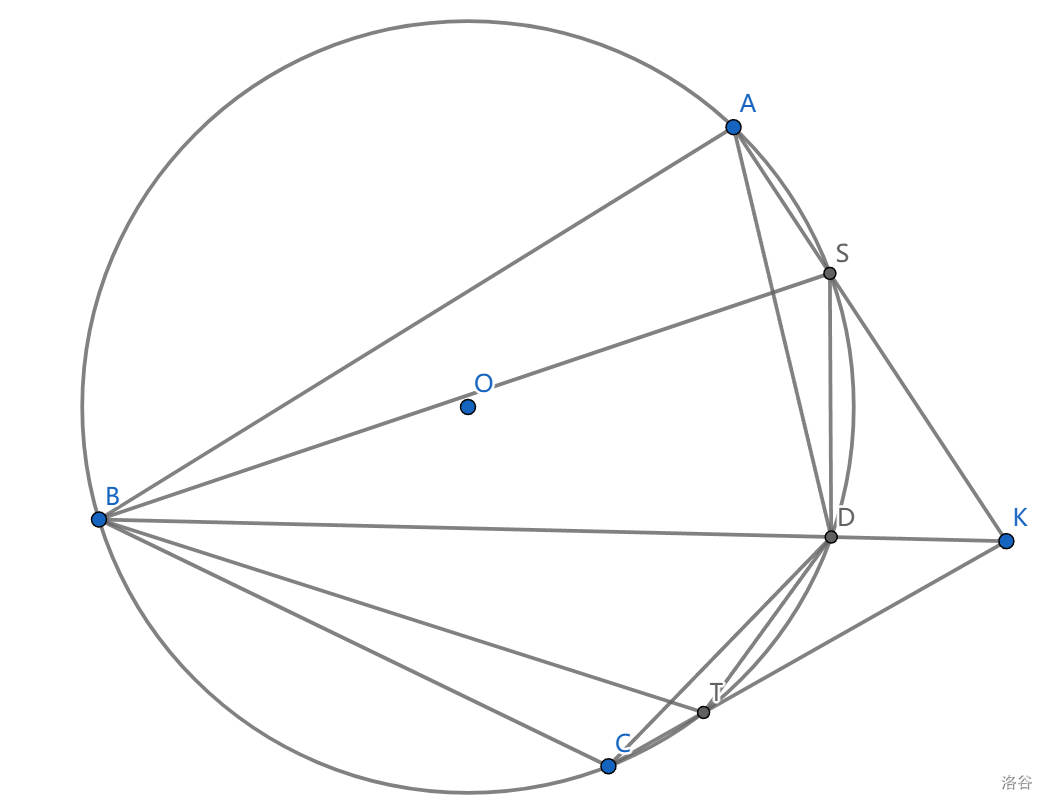
取调和四边形 \(ABCD\) 对角线 \(BD\) 上一点 \(K\) ， \(KA,KC\) 与圆的交点为 \(S,T\) ，则 \(SBTD\) 也是调和四边形。

证明：我们只要证明 \(AT\cap CS\) 在 \(BD\) 上，这样，使用上一章的引理 \(9.3\) ，我们看到 \(AT\cap CS,ST\) 极点与 \(AC\) 极点共线，这就是 \(BD\) ，说明 \(ST\) 极点在 \(BD\) 上。

对 \(AATCCS\) 用 \(Pascal\) 即可。

例1

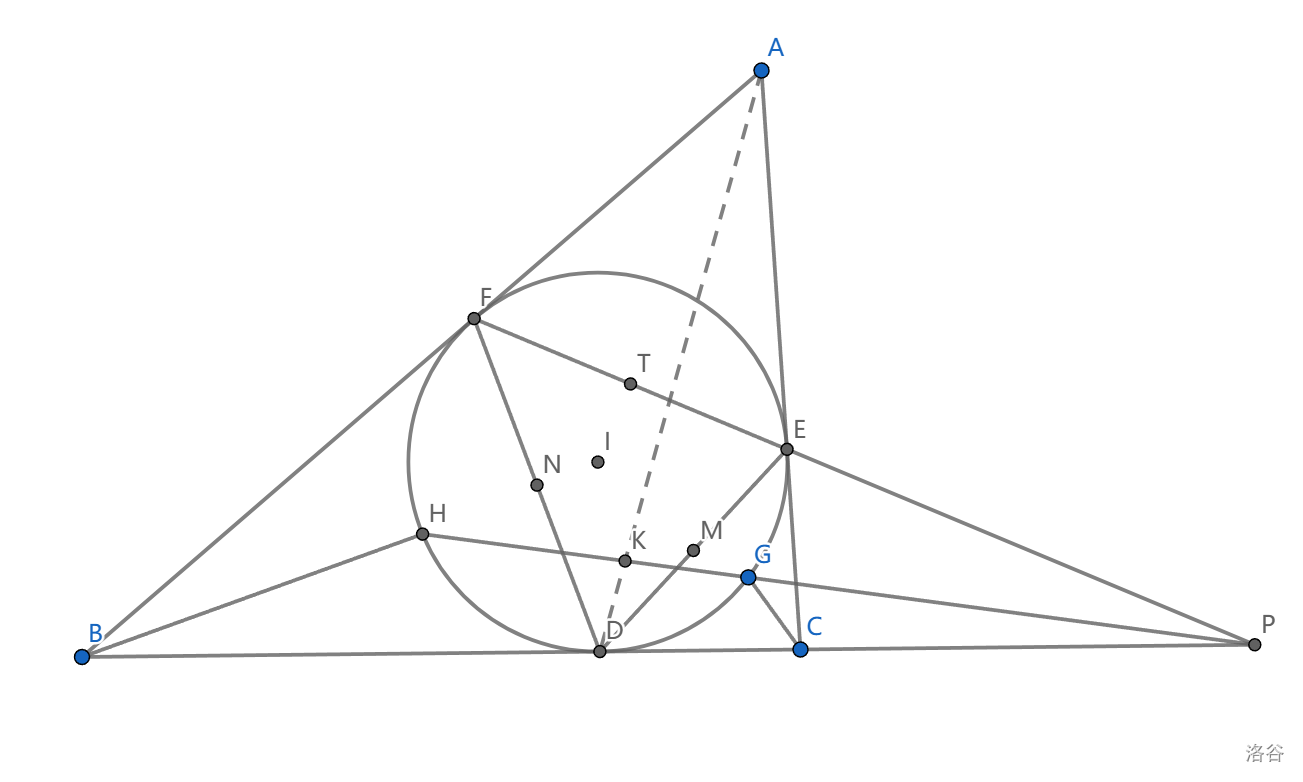
如图， \(I\) 是 \(\triangle ABC\) 的内心， \(AB>AC\) ，内切圆切点为 \(D,E,F\) ，\(EF\cap BC=P\) ，过 \(P\) 的动直线交内切圆于 \(G,H\) ， \(N,M\) 分别是 \(DE,DF\) 的中点， \(Q=\odot (IMG)\cap \odot (INH)\) 。求证： \(Q\) 在定圆上。

这个定圆是什么？取两圆相切（直观理解运动的过程，显然会存在这样的一个瞬间）就是 \(I\) ，取 \(GH=EF\) 会得到 \(EF\) 中点 \(T\) ，当然还有点 \(D\) ，所以是 \(\odot DIT\) （这个圆上还有 \(P\) 之类的点）

首先可以关于内切圆反演，看到 \(B\leftrightarrow N,C\leftrightarrow M,A\leftrightarrow T\) ，圆上的点不变

所以 \(Q=\odot (IMG)\cap \odot (INH)\leftrightarrow BH\cap CG\) ， \(\odot (DIT)\leftrightarrow AD\) ，只要证 \(AD,BH,CG\) 共点。

可以看到调和点列 \((B,C;D,P)=-1\) （用一下梅氏即可），如果共点，通过透视，可以得到 \((H,G;K,P)=-1\) ，所以只要证这个调和点列就行了，然后用调和线束共点（准确地说，只要交比相同就一定共点，被称为 \(Prism Lemma\)）

而 \(AD\) 是 \(P\) 关于内切圆的极线。这个很容易证明，因为 \(P\) 在 \(A\) 的极线上，用极线的共轭性质，而 \(PD\) 本来就是切线。

还有一种理解，我们对 \(\triangle FHB,\triangle EGC\) 用笛沙格定理，只要 \(FH\cap EG\) 在 \(AD\) 上，这就是 \(Brocard\) 定理（还是得证明 \(AD\) 是极线）

注：可以不反演做。取 \(I\) 在两个小圆上的对径点 \(L,K\) ，说明 \(P,K,L,Q\) 共线就可得到 $\angle PQI=Rt\angle $ ，这个共线由 \(DDHEFG,DDEHGG,DDFGHH\) 的 \(Pascal\) 定理给出。

例2

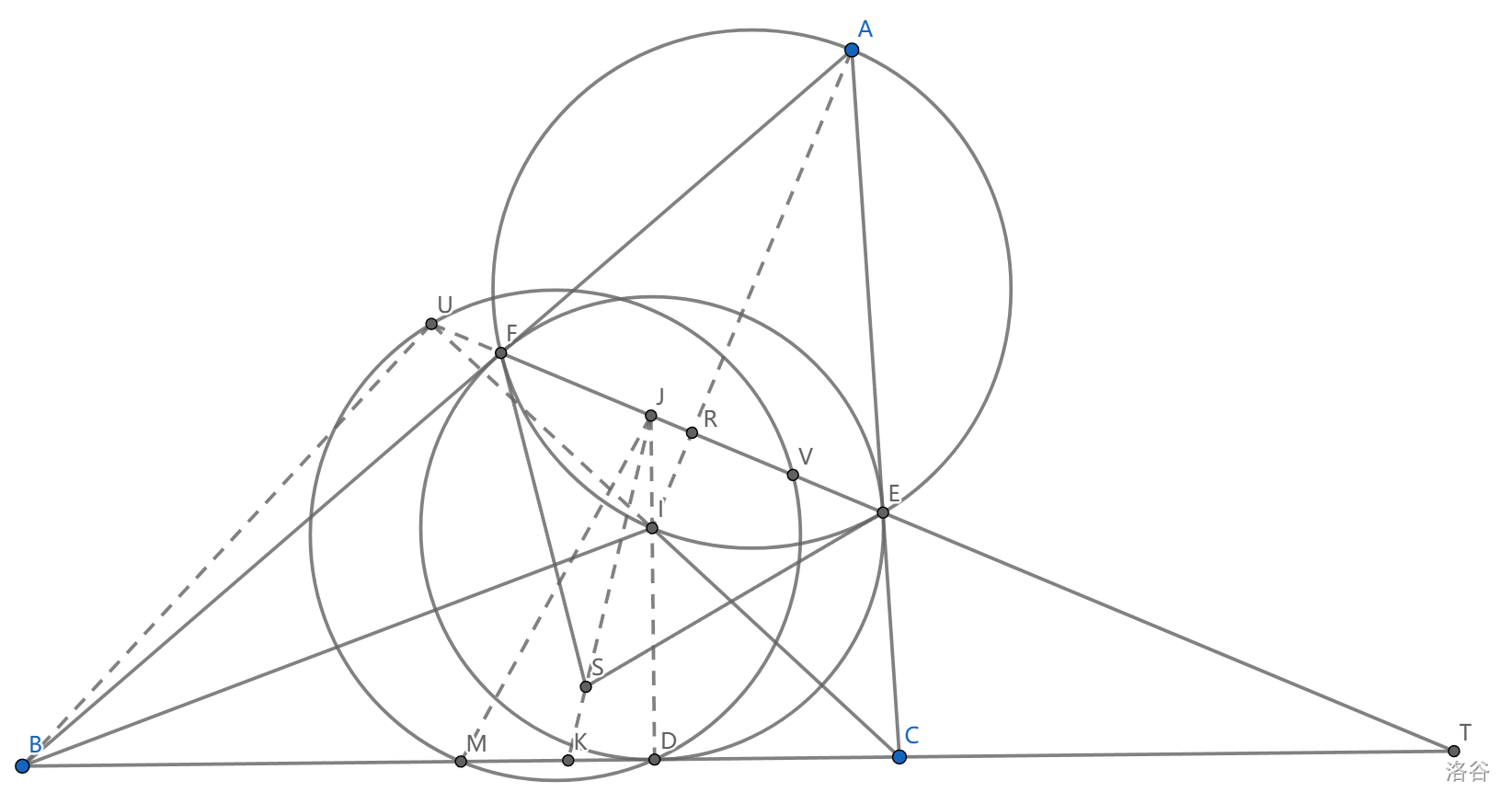
如图，过 \(E,F\) 作 \(\odot (AEF)\) 切线交于点 \(S\) ，求证：以 \(ST\) 为直径的圆与 \(\triangle BCI\) 的九点圆正交。

很明显我们应当证明 \(S,T\) 关于这个圆共轭。我们称这个九点圆为 \(c\) 。

我们试图寻找一些九点圆上的点，比如 \(B\) 到 \(CI\) 的垂足，可以观察到它在 \(EF\) 上。这一性质的证明不困难，设 \(U=CI\cap EF\) ，于是 \(\angle FUI=\angle B/2=\angle FBI\) ，得到 \(FUIB\) 共圆，从而 $\angle BUI=Rt\angle $

于是三条高线 \(BU,ID,CV\) 交于一点。我们不关心这个点，而是看到了完全四边形的调和点列构型： \((U,V;J,T)=-1\) ，说明了 \(J\) 在 \(T\) 的极线上

我们还要利用一下 \(S\) 的性质。有调和点列 \((A,I;R,S)=-1\) ，我们要证 \(JS\) 是极线的话，可以考虑透视到 \(BC\) 得到 \((M,D;K,T)=-1\)

我们说明 \(M\) 就是中点（或者说中点在 \(AJ\) 上），只要证 \([\triangle ABJ]=[\triangle ACJ]\) ，等价于说 \(AB\cdot JF=AC\cdot JE\) ，而 \(\frac{JF}{JE}=\frac{\sin\angle FIJ}{\sin\angle EIJ}=\frac{\sin\angle ABC}{\sin\angle ACB}\)

进一步地， \(M\) 在 \(c\) 上，所以 \(ADM\) 是一条 \(c\) 的割线， \(K\) 在极线上，然后 \(S\in JK\) 与 \(T\) 共轭。

例3

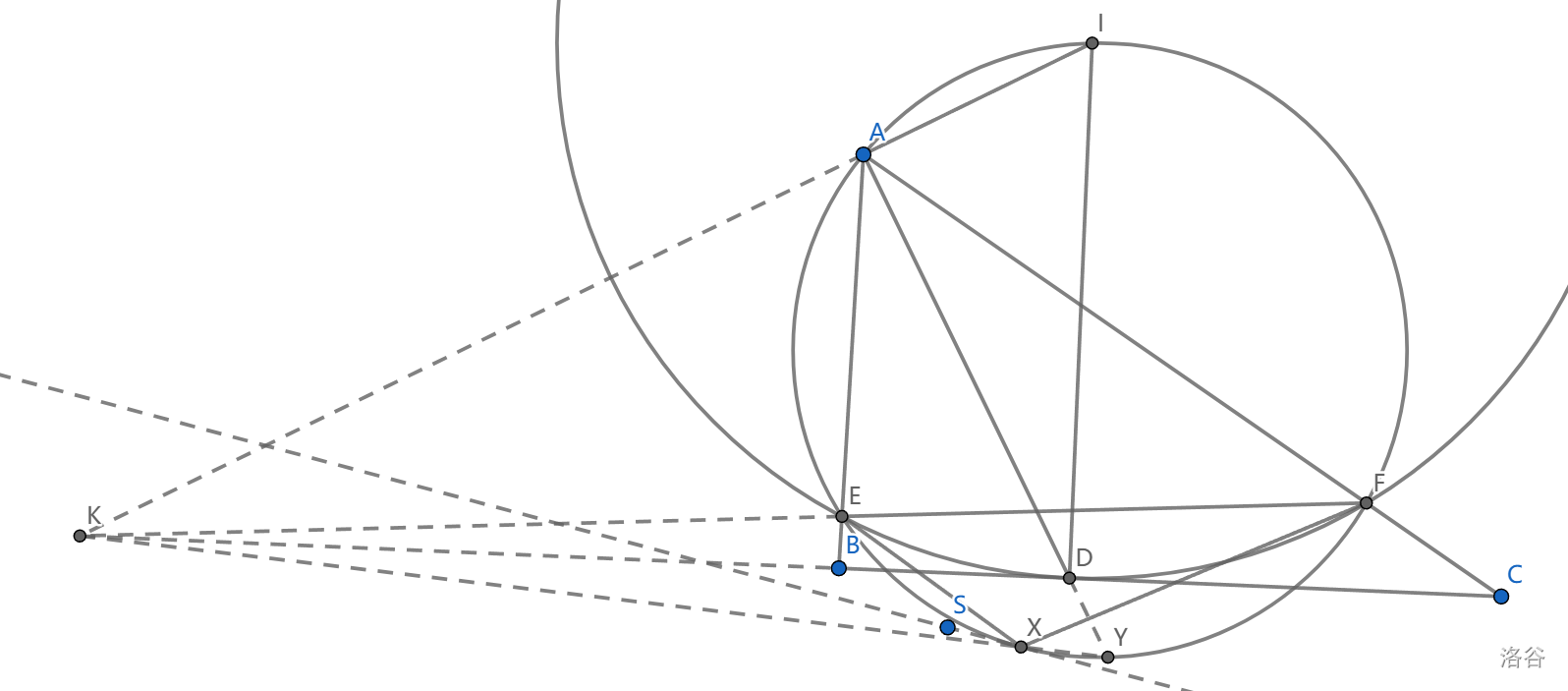
如图， \(AD\) 是 \(\triangle ABC\) 的角平分线，点 \(I\) 满足 \(AI\perp AD,DI\perp BC\) ，\(\odot I\) 以 \(ID\) 为半径，交 \(AB,AC\) 于 \(E,F\) ， \(X\) 在 \(\odot (AEF)\) 上，满足 \(AEXF\) 是调和四边形。求证： \(\odot (AEF)\) 与 \(\odot (BXC)\) 切于点 \(X\)

首先 \(IAEF\) 共圆，并且 \(I\) 是弧 \(EAF\) 中点，因为它在 \(EF\) 中垂线上，以及 \(\angle AID=Rt\angle -(B-C)/2\)

我们拥有角平分线 \(AD\) 以及 \(AI\perp AD\) ，这是一个很明显的阿氏圆构型，延长 \(IA\cap BC=K\) ，于是 \((B,C;K,D)=-1\)

\(EF\) 也过点 \(K\) ，为了证明这一点，我们需要设 \(K'=EF\cap BC\) 。我们计算 \(K,K'\) 到 \(\odot (AEF)\) 的圆幂。

由射影定理， \(KA\cdot KI=KD^2\) ，而 \(K'D\) 是 \(\odot I\) 的切线， \(K'E\cdot K'F=K'D^2\) 。所以 \(K,K'\) 均在点圆 \(D\) 与 \(\odot(AEF)\) 根轴上，但这条根轴很显然不是 \(BC\) ，所以 \(K=K'\)

我们要利用调和四边形的条件，根据引理 \(11.1\) ，我们延长 \(KX\) 交圆于 \(Y\) ，因为 \(KAI\) 是割线，所以 \(IEFY\) 是调和四边形，而 \(I\) 是弧 \(EIF\) 中点，所以 \(Y\) 是弧 \(BC\) 中点，进一步地， \(ADY\) 共线。

因为 \(K\) 在点圆 \(D\) 与 \(\odot(AEF)\) 根轴上，所以 \(KD^2=KX\cdot KY,\triangle KDX\sim\triangle KYD\) ，所以 \(\angle KDX=\angle KYD\overset{}{=}\angle XYA\overset{AEXY共圆}{=}\angle BEX\) ，所以 \(BEDX\) 共圆。同理 \(CFDX\) 共圆。

我们任取切线在 \(X\) 左侧的一点 \(S\) ，然后 \(\angle BXS=\angle EXS-\angle BXE\overset{BEDX,CFDX 共圆}{=}\angle EFX-\angle BDE\overset{BD为切线}{=}\angle EFX-\angle EFD=\angle DFX\overset{CFDY共圆}{=}\angle DCX=\angle BCX\)

这就说明 \(XS\) 也是 \(\odot (BCX)\) 的切线，证毕。

例4

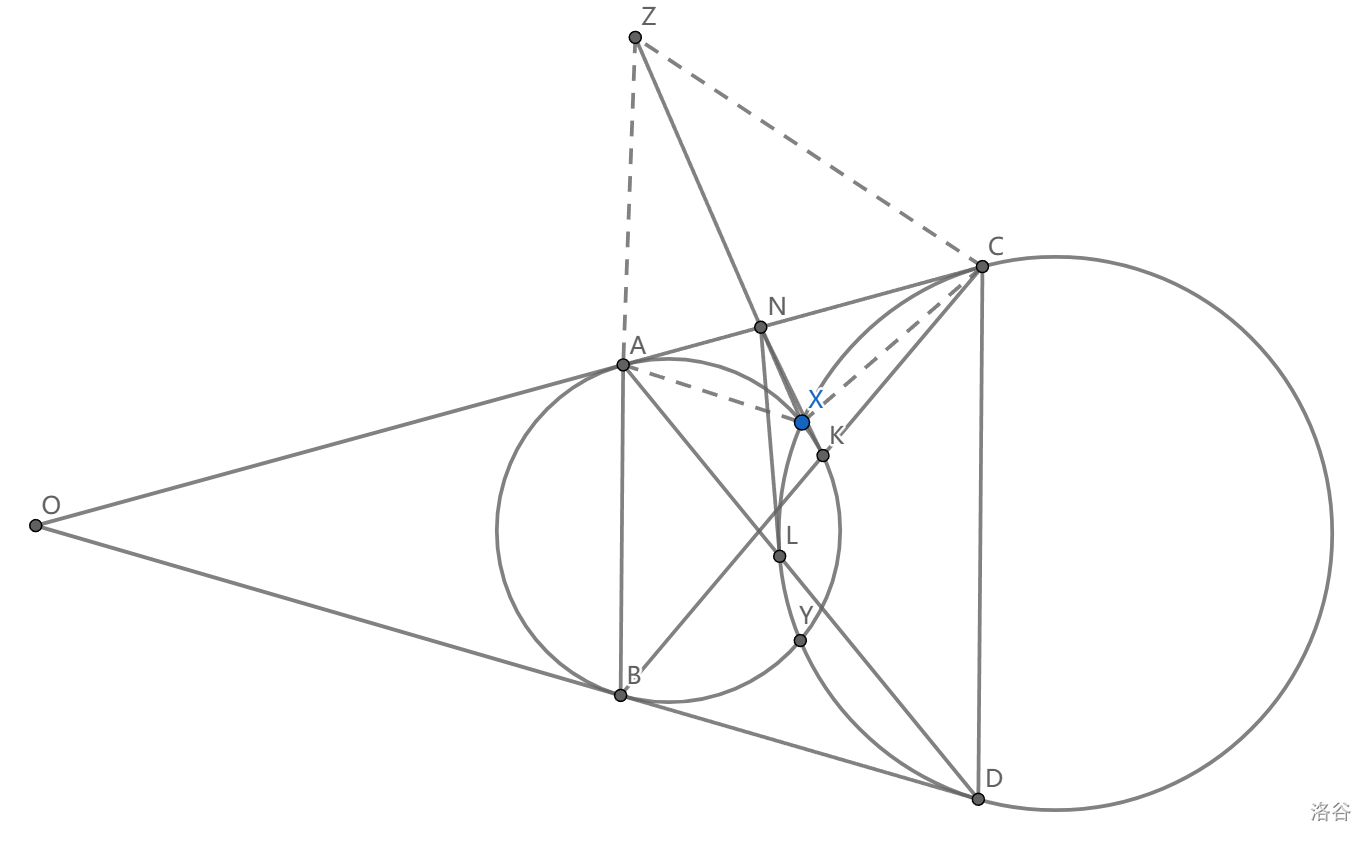
如图， \(c_1,c_2\) 交于 \(X,Y\) 两点， \(AC,BD\) 是两条外公切线，点 \(Z\) 是 \(Y\) 关于 \(AC\) 的对称点，\(AD\cap c_1=L,BC\cap c_2=K\) ，求证：过 \(K\) 作 \(c_1\) 切线，过 \(L\) 作 \(c_2\) 切线，直线 \(XZ\) 交于一点。

一个好的图可以看出这个点在 \(AC\) 上。我们最好的希望就是我们只要处理 \(AC\cap ZK=N\) ，然后处理 \(L,K\) 中的一个，另一个同理完成。

延长 \(AC,BD\) 交于点 \(O\) 。似乎 \((A,C;O,N)=-1\) ，不过没什么证明的思路。我们还是先研究关键的点 \(Z\) ，它需要一些刻画

熟悉外公切线和根轴的读者很快就会说， \(\angle AXC+\angle AYC=\pi\) ，这个导角通过弦切角能轻松完成，从而 \(AZCX\) 共圆。

我们关于 \(O\) 做一个 \(c_1\leftrightarrow c_2\) 的反演，当然本质是关于 \(O\) 导一些圆幂，但是利用反演可以更加直观一些。注意 \(O\) 是外位似中心。

\(A\leftrightarrow C,B\leftrightarrow D,X,Y\) 不变，于是 \(OX^2=OA\cdot OC,\triangle OXA\sim \triangle OCX\) ，然后 \(\frac{AX}{XC}=\sqrt\frac{OA}{OC}=\sqrt\frac{r_1}{r_2}\)

我们还看到 \(\frac{AZ}{ZC}=\frac{AY}{YC}=\sqrt{\frac{r_1}{r_2}}\) ，所以 \(AZCX\) 是调和四边形

通过 \(X\) 透视就可以得到 \((A,C;O,N)=-1\) 了，不过我们得证明 \(XO\) 是 \(AZCX\) 的切线。根据刚才反演得到的相似有 \(\angle OXA=\angle ACX\) ，这是对的。

最后做 \(K\) 的切线，交 \(AC\) 于点 \(M\) ，我们要证 \((A,C;M,O)=-1\) ，这并不困难，\(M\) 是 \(AK\) 的极点，如果交 \(c_1\) 于 \(E\) ，我们从 \(B\) 透视调和四边形 \(BAEK\) 就可以得到。