共轭中线

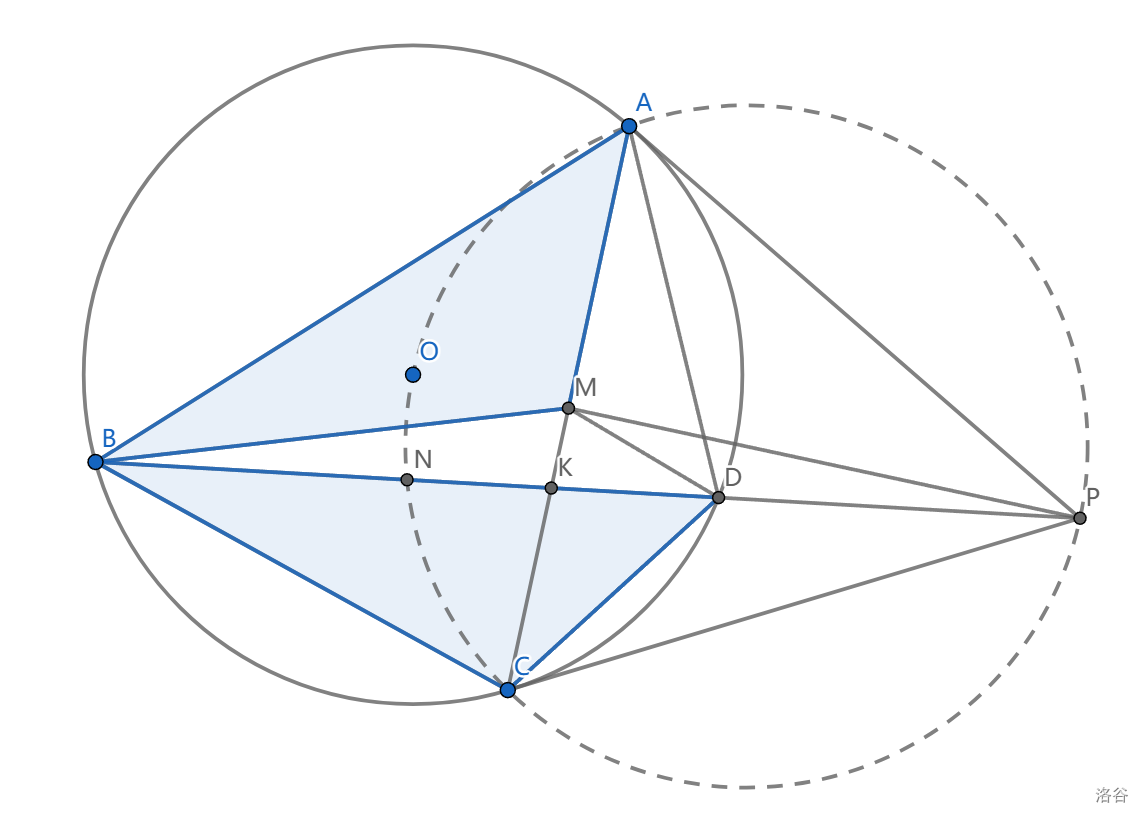
\(K\) 在 \(BC\) 上， \(M\) 是 \(BC\) 中点，满足 \(AK,AM\) 为等角线，则称 \(AK\) 为 \(\triangle ABC\) 的共轭中线

延长 \(AK\) 交 \(ABC\) 外接圆于点 \(D\) ，则得到调和四边形 \(ABCD\) 。调和四边形是指 \(AB\cdot CD=AC\cdot BD\) 的圆内接四边形。

我们有如下的性质：

1. （共轭中线的做法）\(P\) 是 \(AC\) 的极点，则 \(PBD\) 共线

2. \(M,N\) 是 \(ABCD\) 的等角共轭点（任一点向两个点连线，都是这个角的等角线），从而 \(BC\) 也是 \(\triangle ABD\) 的共轭中线（对其它几个点都是如此）

3. \(\triangle BCD\sim \triangle BMA\) ，进而 \(ABCD\) 是调和四边形。

4. \(\frac{AK}{KC}=(\frac{BA}{BC})^2\)

5. \(ACPN\) 共圆

6. \((B,D;K,P)=-1,MK\) 平分 \(\angle BMD\) （前者是极线构型的调和点列，后者是这个调和点列用阿氏圆推导的结论）

关于调和四边形的判定，以下这些比较常见：

1. 对边乘积相等

2. 从某一条共轭中线得到

3. \(B,D,P\) 共线，其中 \(P\) 是 \(AC\) 的极点

4. 利用调和点列透视，以及 \(MK\) 平分 \(\angle BMD\) 结合圆内接通过调和点列再推到调和四边形

5. 对角线中点是等角共轭点（无需共圆）

因为 \(AK\) 是共轭中线，用同一法交圆于 \(C'\) ，此时根据等角线性质 \((\frac{AB}{AD})^2=\frac{BK}{KD}=(\frac{CB}{CD})^2\) ，所以 \(C=C'\) （说明其实不需要等角共轭这么强的条件，只要两组等角线就够了）

此外共轭中线可以直接（不经过调和四边形）利用性质 \(4\) 判定。

在射影几何中介绍了更多调和四边形的问题。与射影几何无关的共轭中线问题不是很多。

要注意对称，等腰梯形这类结构，这些地方经常出现共轭中线。

例1

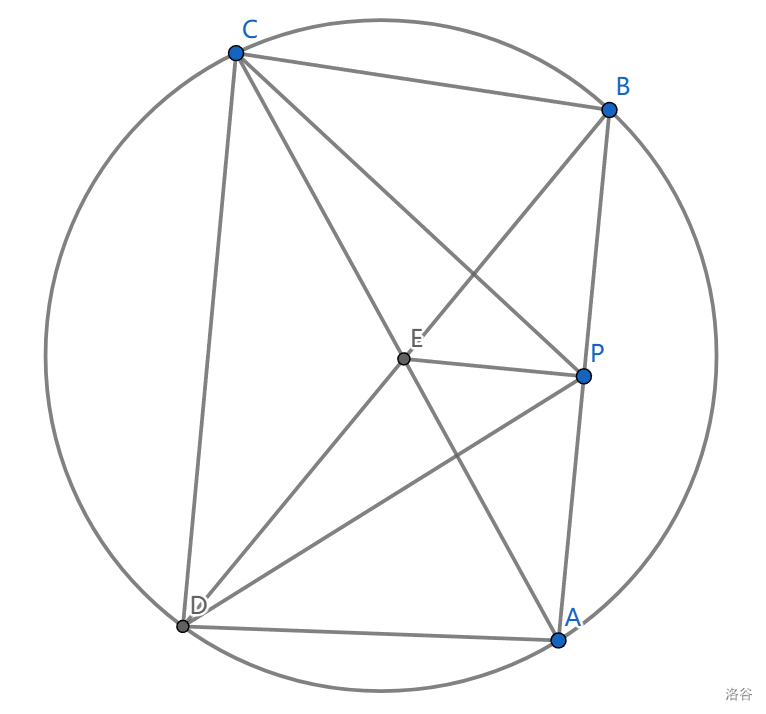
如图，圆内接四边形 \(ABCD\) 满足 \(AD^2+BC^2=AB^2\) ， \(E=AC\cap BD\) ，点 \(P\) 在 \(AB\) 上，满足 \(\angle APD=\angle BPC\) ，求证： \(PE\) 平分线段 \(AB\) 。

关键的条件在这个条件的利用。我们会分拆 \(AB^2=AB\cdot AP+AB\cdot BP=AD^2+BC^2\)

我们设某点 \(P'\) 在 \(AB\) 上，满足 \(AB\cdot AP'=AD^2,AB\cdot BP'=BC^2\) ，就会有 \(\triangle ADP'\sim\triangle ABD,\triangle BCP'\sim \triangle BAC\) ，从而 \(\angle AP'D=\angle ADB=\angle ACB=\angle CP'B,P=P'\)

接下来要证 \(PE\) 是 \(\triangle CED\) 中线，这里用一个小结论，我们只要证 \(EP\) 是 \(\triangle EAB\) 的共轭中线就可以了（把中线转换成 \(\frac {CE}{DE}=\frac{\sin \angle DEP}{\sin \angle CEP}\) ，然后转化成 \(A,B\) 相关的命题）

而 \(\large\frac{PA}{PB}=\frac{\frac{AD^2}{AB}}{\frac{BC^2}{AB}}=(\frac{AD}{BC})^2=(\frac{AE}{BE})^2\) ，这就完成了证明。

例2

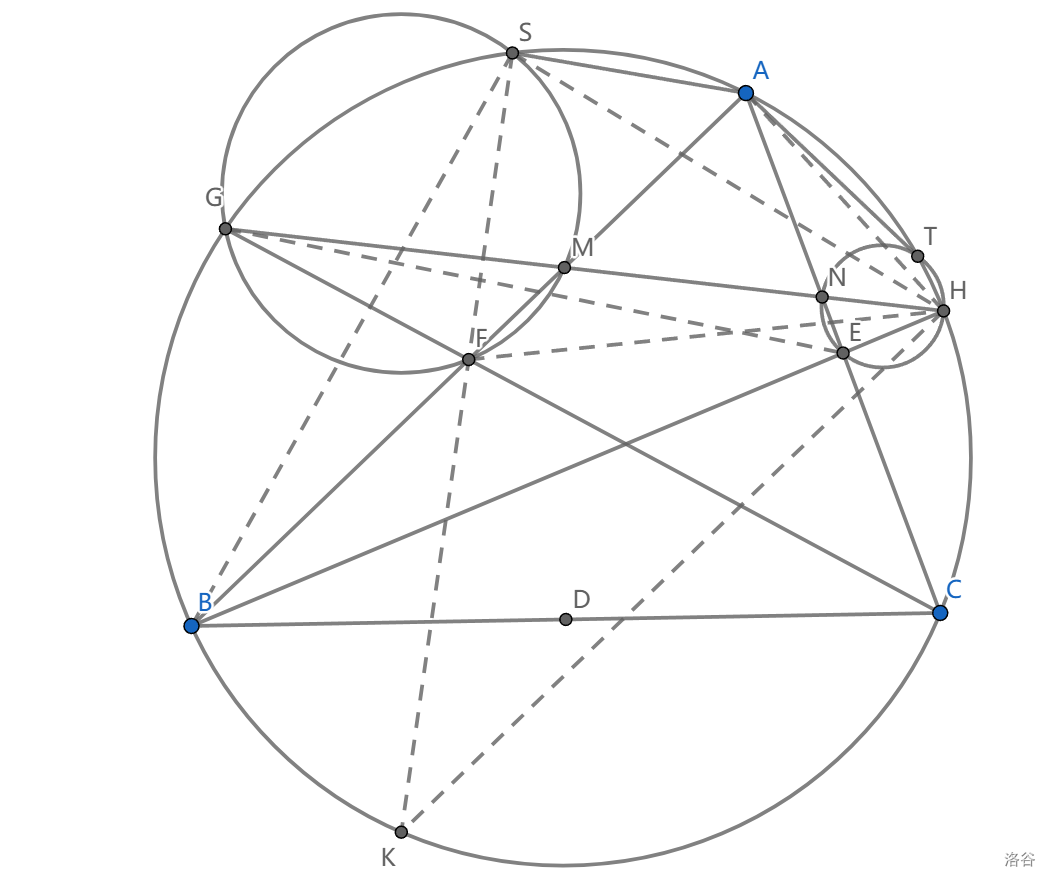
如图， \(\triangle ABC\) 边的中点依次为 \(D,E,F\) ， \(BE,CF\) 分别交外接圆于 \(H,G\) ， \(GH\) 与 \(AB,AC\) 交于 \(M,N\) ， \(\triangle GMF,\triangle HNE\) 的外接圆与 \(\triangle ABC\) 的外接圆交于 \(S,T\) ，求证： \(AS=AT\)

这道题我们会介绍一个经常出现的调和四边形。

我们很显然应当考虑 \(AS,AT\) 的圆周角。我们将要利用两圆相交，如果考虑长度，那有可能是根轴圆幂，旋转相似之类的，不过这里不是很好直接看出这些方法的前途，我们来试试 \(Reim\) 引理构造平行。

\(SF\) 看上去更靠谱一些，可以给出 \(KH//ME\) ，从而 \(KH//AB\) 给出等腰梯形（不是所有 \(Reim\) 引理都能得到等腰梯形的！这是一个不平凡的事情）。我们也许应当将 \(S,T\) 放在一起考虑，但这张图里实在是找不出什么三线共点包括了 \(S,T\) 的，所以暂且只看看 \(S\)

等腰梯形 \(AHKB\) 里有什么呢？，我们有 \(SEK\) ，这里 \(KES\) 是中线，关于 \(AB\) 的中垂线对称，我们将看到 \(HS\) 是 \(\triangle HAB\) 的共轭中线！

这很容易理解，因为中线与圆的交点和共轭中线与圆的交点关于这条边的中垂线对称。所以 \(ABHS\) 是调和四边形，我们看到 \(\angle AHS=\angle BHE\)

这就将问题转换为了 \(\angle BHE=\angle CGH\) ，只要 \(EFGH\) 共圆。这很容易， \(\angle CFE=\angle BCG=\angle BHG\) ，证毕。

例3

如图， \(\triangle ABC\) 边 \(BC\) 上有一点 \(D\) ， \(P=BI\cap (ABD),Q=CI\cap (ACD)\) ，若 \(S_{\triangle PID}=S_{\triangle QID}\) ，证明： \(PI\cdot QD=QI\cdot PD\)

\(P\) 在 \((ABD)\) 是弧 \(AD\) 的中点， \(Q\) 在 \((ACD)\) 是弧 \(AD\) 中点，这说明了实际上 \(A,D\) 关于 \(PQ\) 对称。

首先 \(APIQ\) 共圆，因为 \(\angle API=\angle ADB,\angle AQI=\angle ADC\)

接下来如何处理对称条件，还有面积条件呢？对称条件的常见处理方法是，延长 \(DI\) 交 \(PQ\) 于 \(M\) ，那么 \(PQ\) 平分 \(\angle AMD\) 。此外由面积条件， \(M\) 实际上是 \(PQ\) 的中点

我们要证的是 \(AQ\cdot PI=AP\cdot QI\) ，也就是调和四边形。在对称图形里其实很好证明，因为 \(AM\) 与 \(DIM\) 关于 \(PQ\) 对称，所以设 \(AM\cap \overset{\frown}{PQ}=J\) ，由对称性，我们看到弧 \(IQ=PJ\) ，然后 \(AI\) 就是共轭中线。

例4

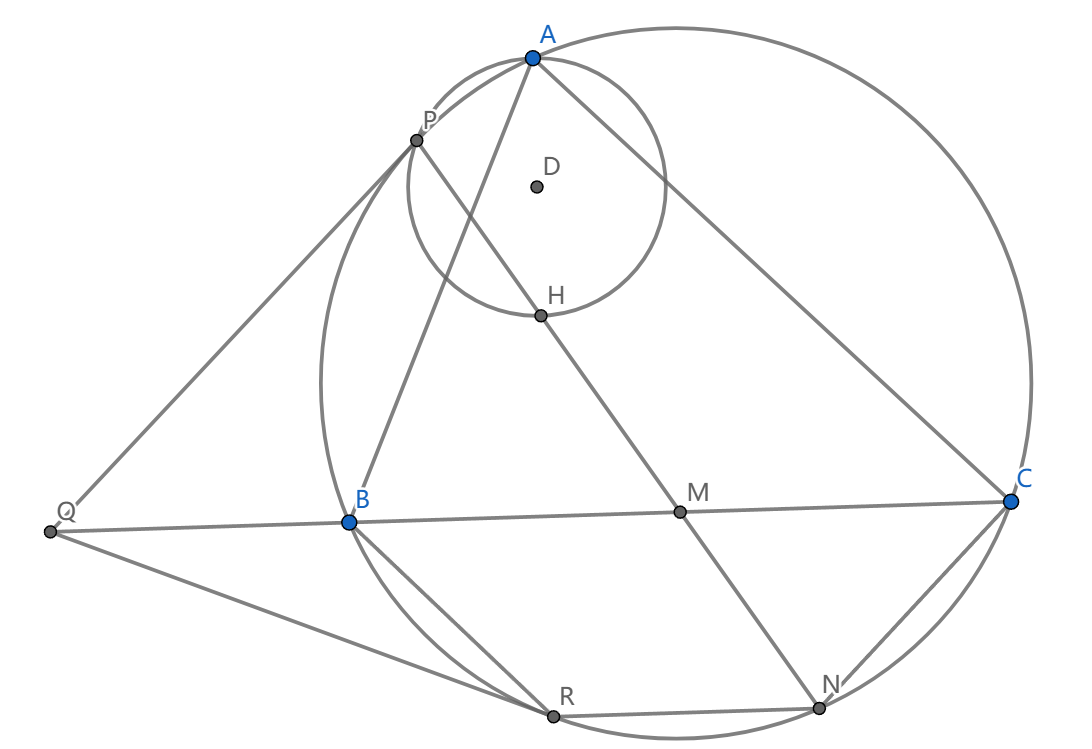
如图， \(\triangle ABC\) 中， \(H\) 是垂心，以 \(AH\) 为直径的圆与 \((ABC)\) 交于 \(P\) ，过 \(P\) 作 \((ABC)\) 切线交 \(BC\) 于 \(Q\) 。证明： \(QP=QH\)

我们取 \(A\) 的对径点 \(N\) ，熟知 \(PHMN\) 共线。我们取 \(H\) 关于 \(BC\) 的对称 \(R\) ，只要证 \(QP=QR\) ，换而言之只要证 \(QR\) 是切线

而 \(QR\) 是切线等价于说 \(PBCR\) 是调和四边形，注意看这里的等腰梯形 \(BCNR\) ，所以说 \(\angle CPM=\angle BPR\) ，这就证毕。