内心与相关构型

内心

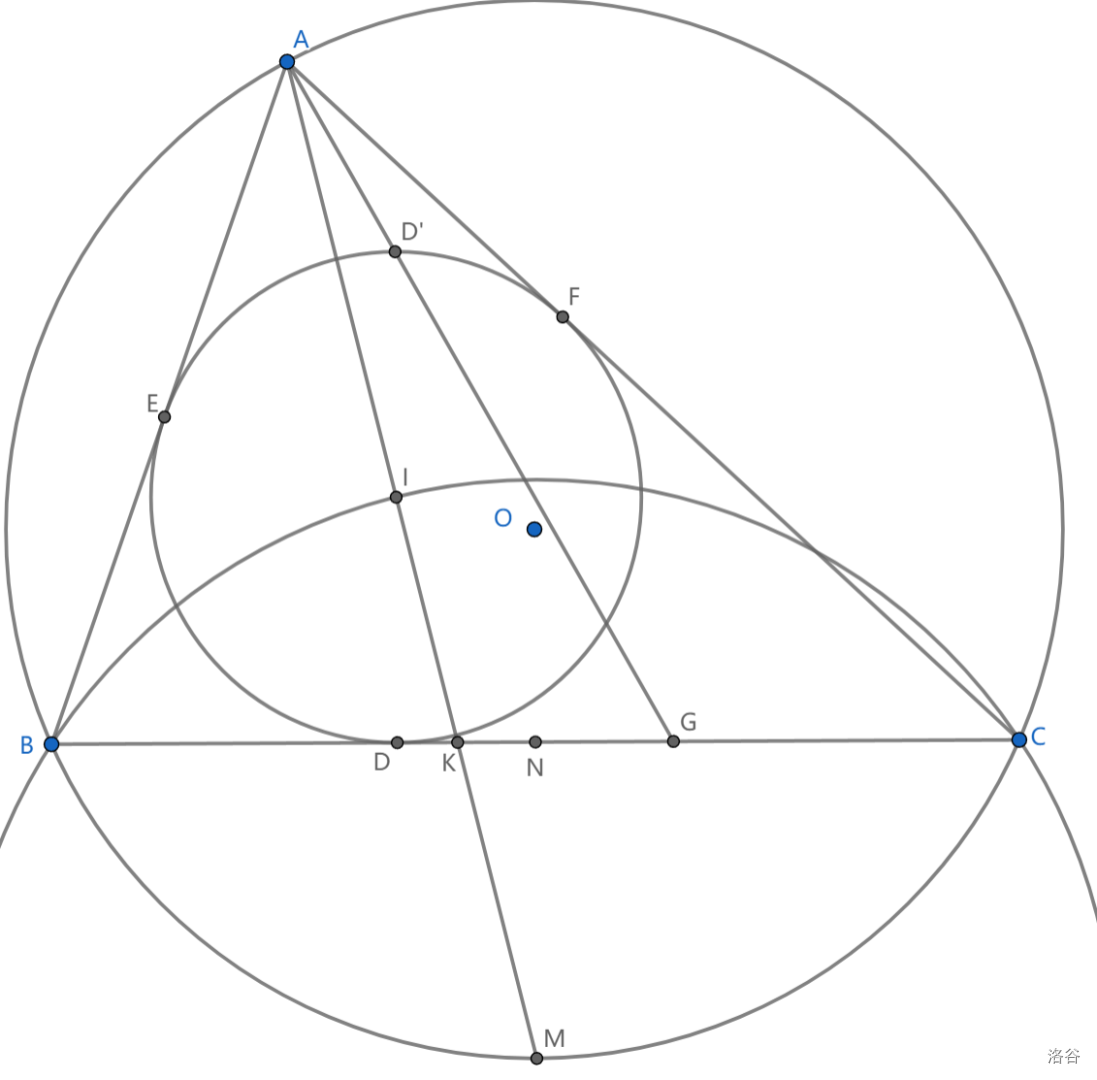
1、三条角平分线

2、在 \(\odot M\) 上（鸡爪圆上）

3、\(AI\cdot IM=AM\cdot IK=2Rr\) ，即 \(OI^2=R^2-2Rr\)

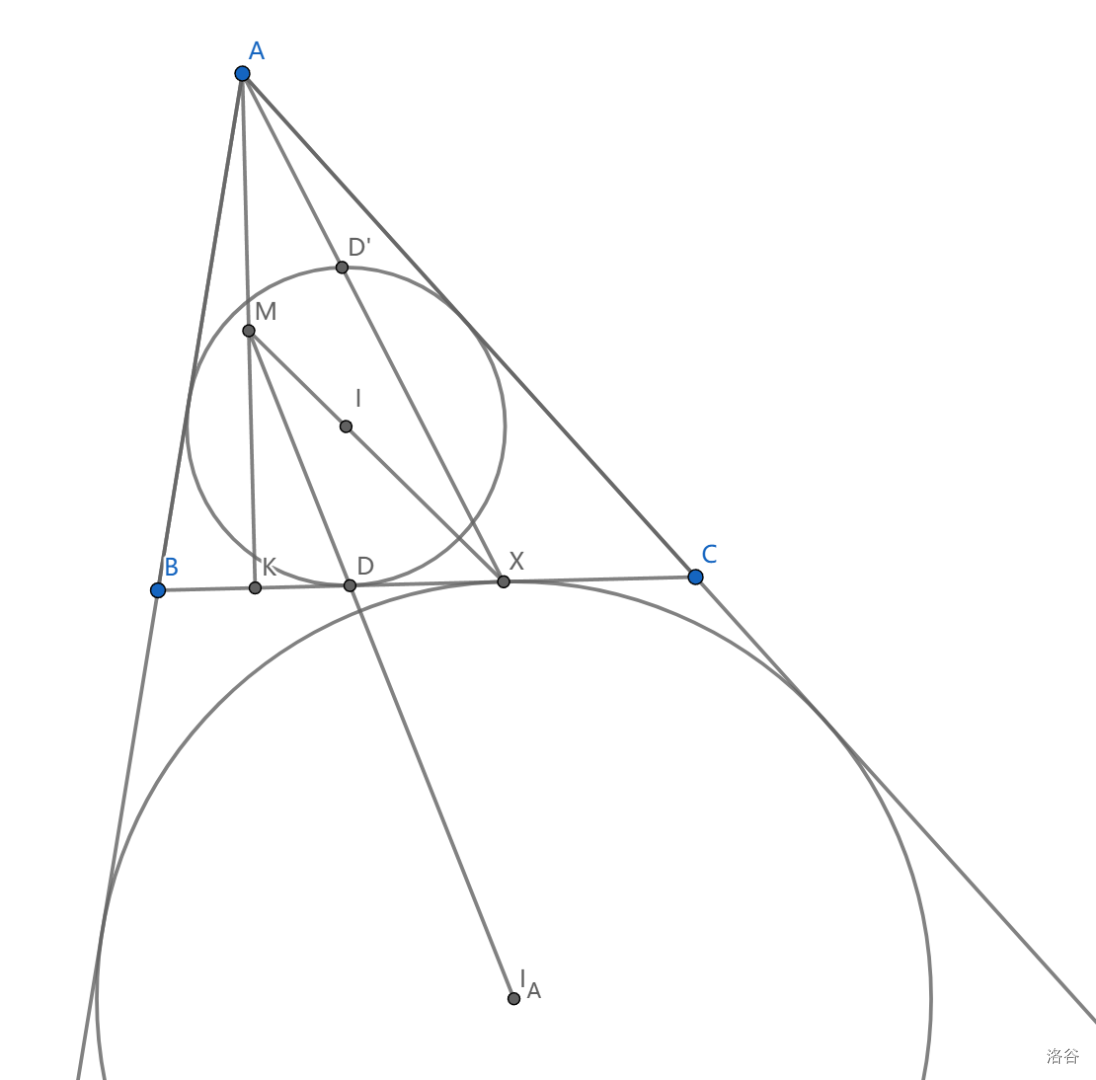
4、\(\odot I\) 与 \(\odot I_A\) 关于点 \(A\) 位似，所以 \(D\) 的对径点 \(D'\) 满足 \(AD'X\) 共线（两个圆过这两个点的切线平行），同理 \(AD\) 过 \(X\) 的对径点

必须要指出，关于 \(A\) 的位似还能给出鸡爪圆

5、设 \(N\) 是 \(BC\) 中点，则 \(IN//AX\) （利用中位线即可）

6、\(XI,I_AD\) 交于 \(AK\) 的中点，其中 \(I_AD\) 与内切圆的交点 \(N\) 满足 \(BCN\) 外接圆与内切圆相切

利用 \(\triangle XDE\) 与 \(\triangle XKA\) 位似，其中 \(I,M\) 都是中点，所以是位似对应点， \(XIM\) 共线， \(I_ADM\) 同理。

第二个取出 \(P=NK\) 与 \(BC\) 中垂线交点，证明它与 \(BCN\) 共圆（用圆幂，其中 \(NK\cdot KP\) 里用到 \(\angle NKB\) 会消掉的）即可

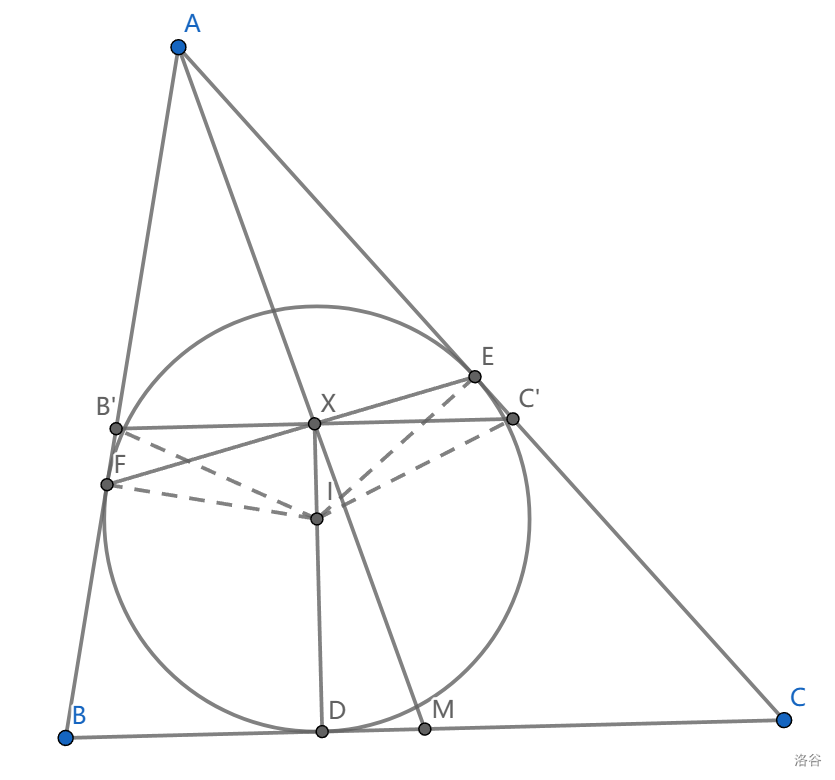
7、\(AM,ID,EF\) 共点

这个证明有点难度。我们要构造过 \(X=DI\cap EF\) 平行于 \(BC\) 的直线，假设它是 \(B'C'\) 。然后我们看到 \(B'FIX,C'EXI\) 共圆

所以 \(\angle FB'I=\angle FXI=\pi-\angle EXI=\angle IC'E\) ，说明 \(\triangle IB'F\cong \triangle IC'E\)

并且 \(\angle IB'X=\angle IFX=\angle IEX=\angle IC'X\) ，也就是 \(IB'=IC'\) ，而 \(\angle B'XI=Rt\angle\) ，所以 \(B'X=XC'\)

现在 \(X,M\) 是 \(\triangle AB'C',\triangle ABC\) 的相似对应点，所以 \(AXM\) 共线

（这个构型不是非常重要，了解即可）

8、\(\triangle INK \sim \triangle IDA\)

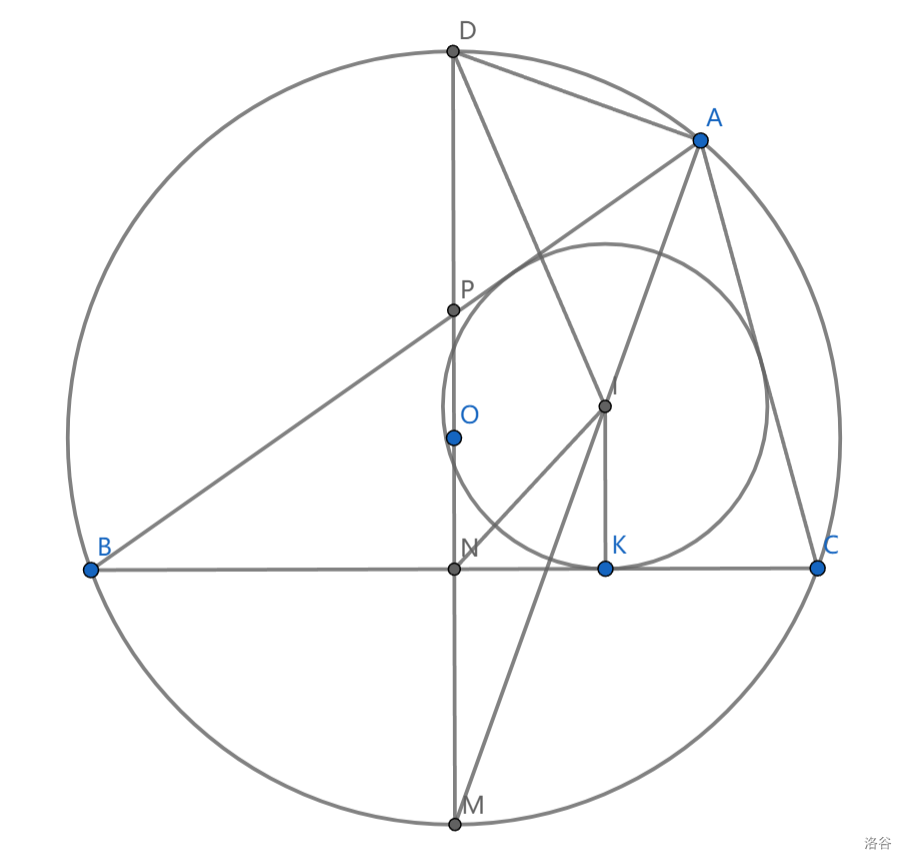
9、\(ND\) 中点 \(P\) 满足 \(PA=PK\)

10、取 \(\overset{\frown}{AB}\) 与 \(\overset{\frown}{AC}\) 的中点可构成平行四边形，且对角线垂直于 \(AI\)

11、\(N\) 在 \(BC\) 上， \(D\) 在外接圆上，若 \(MND\) 共线，则 \(\triangle MNI \sim \triangle MID\) （图示为一种特例）

根据弧中点的性质和鸡爪定理 \(MN\cdot MD=MB^2=MI^2\)

12、\(BI\) 与 \(EF\) 的交点 \(P\) 满足 \(P\) 在 \(AB\) 所对的中位线上，并且 \(BP\perp CP\) （图可见例4）

例1

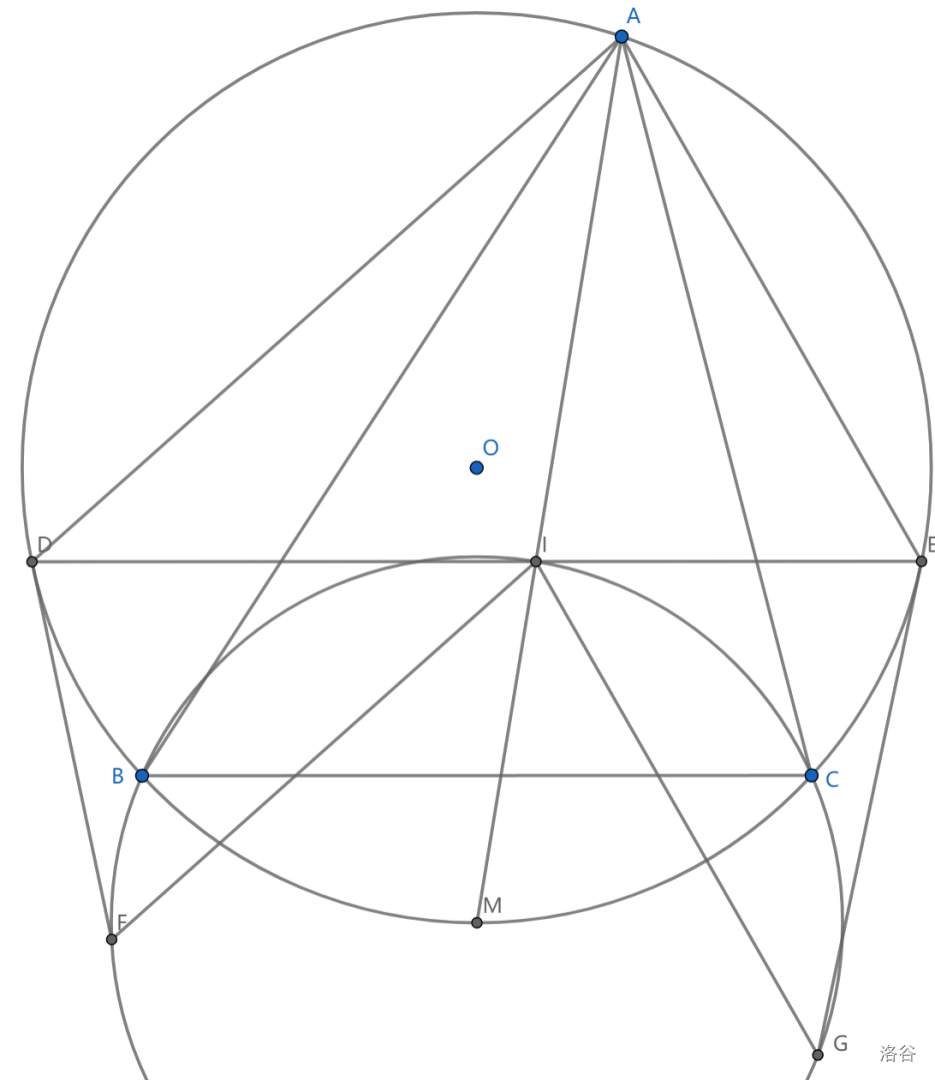
如图， \(I\) 为 \(\triangle ABC\) 内心，过 \(I\) 作 \(BC\) 平行线交外接圆 \(O\) 于 \(D,E\) ，过 \(D,E\) 作外接圆切线，分别与 \(IG // AE\) 交于 \(G\) ， \(IF// AD\) 交于 \(F\) ，求证：\(B,C,F,G\) 共圆

先画出这个圆，就可以注意到 \(I\) 也在这个圆上，即该圆为鸡爪圆

不难注意到本题中的 \(IF//AD\) 构成了 \(Reim\) 引理（平行+共圆=共圆！）的模型（\(DF\) 为切线）

从而 \(IMFD\) 共圆，接下来知道了是鸡爪圆，我们就会考虑处理点 \(M\)

实际上 \(\angle MFI=\angle MDI=\angle MDF=\angle MIF\) ，从而 \(MF=MI\)

同理可证 \(MG=MI\) ，这就证毕。

例2

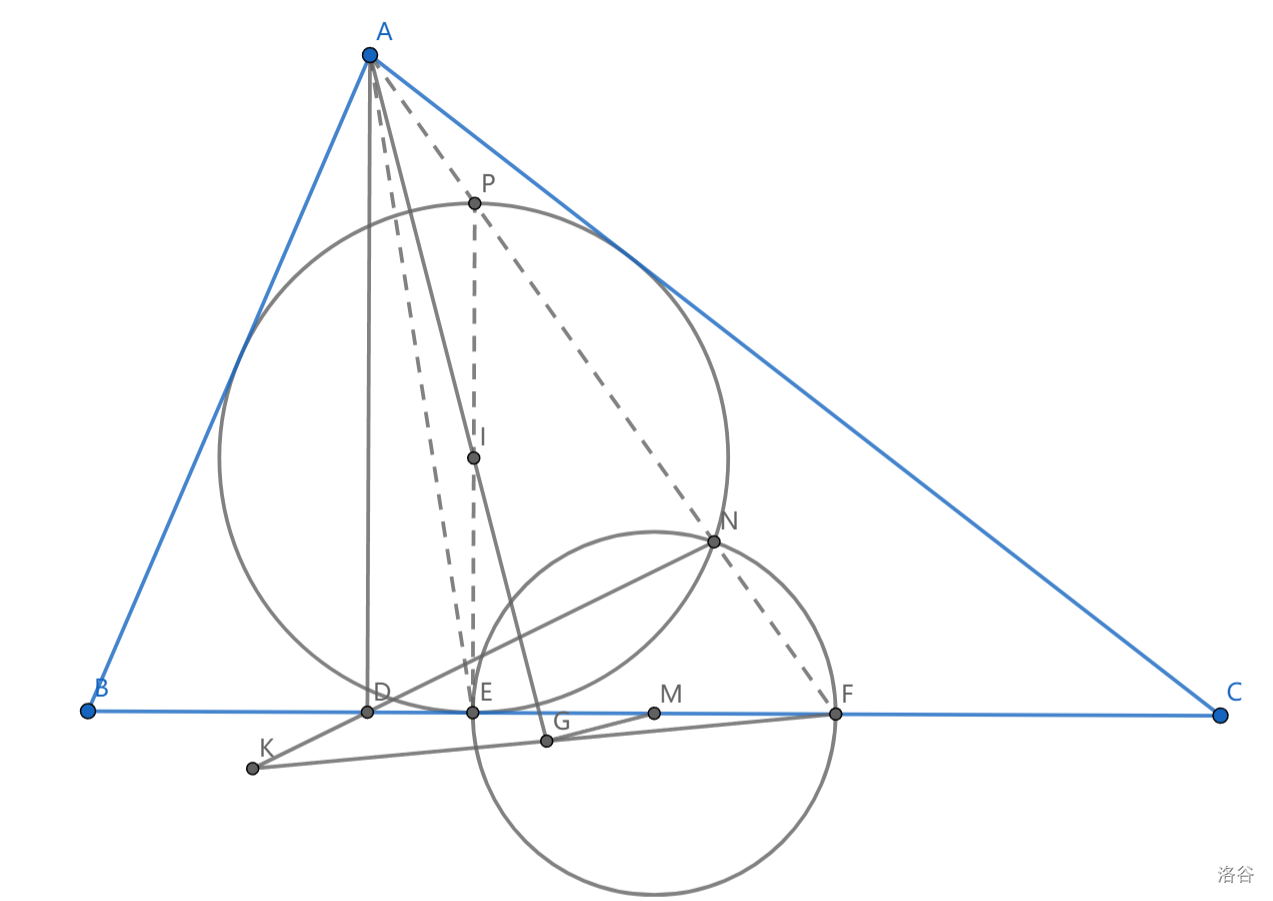
如图，\(AD\perp BC\) 于点 \(D\) ， \(\triangle ABC\) 内切圆 \(I\) 切 \(BC\) 于点 \(F\) ，\(M\) 为 \(BC\) 中点，以 \(M\) 为圆心， \(ME\) 为半径画圆交圆 \(I\) 与 \(BC\) 于 \(N,F\) ，作 \(MG\perp AI\) 于点 \(G\) ，延长 \(FG,ND\) 交于点 \(K\) ，求证： \(D,E,K,G\) 共圆

分析：\(E,F\) 关于 \(M\) 对称，不难想到构造 \(E\) 的对径点，可以发现 \(A,P,N,F\) 共圆，这是因为 \(MI\) 垂直平分 \(EN\) 且为 \(PF\) 对应中位线

借助 \(ANED\) 共圆，由 \(FD\cdot FE=FN\cdot FA\) ，从而只需证 \(ANKG\) 共圆即可

那么只需证 \(\angle AND=\angle AGK\)， 消点 \(K\) 并尽量转移，得到 \(\angle FGM(=)\angle DNE=\angle DAE=\angle APE\) ，可用 \(SAS\) 证明 \(\triangle PAE\sim \triangle MGF\) ，即证

也可用 \(IM//PF\) 和 \(Reim\) 引理得到 \(AEGF\) 共圆，然后导角

例3

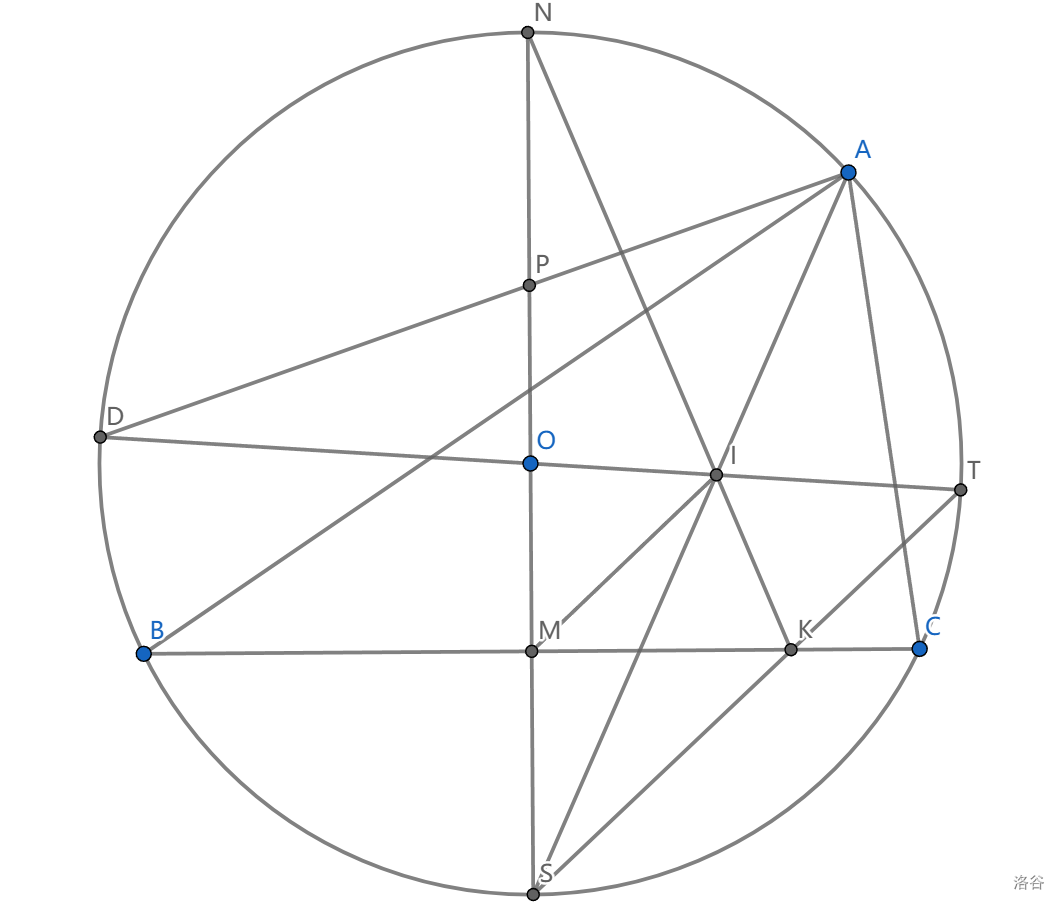
如图， \(O,I\) 分别为 \(\triangle ABC\) 的外心与内心， \(S\) 是弧 \(BC\) 的中点， \(N\) 是弧 \(BAC\) 的中点。延长 \(NI\) 与 \(BC\) 交于点 \(K\) ，直线 \(IO\) 与 \(\odot O\) 交于 \(D,T\) 两点, 已知 \(AD\) 平分线段 \(NI\) ，求证： \(S,K,T\) 共线。

可以用同一法做，会简单一些。

令 \(M=NS\bigcap BC,P=AD\bigcap NI\)

平分的条件如何利用？我们看到一个直角三角形， \(\angle NAS=Rt\angle => PN=PI=PA\)

根据性质 \(11\) ， \(\triangle SMI \sim \triangle SIN\) ，有 \(\angle NIA=\pi -\angle NIS=\pi -\angle IMS\)

由于 \(NS,DT\) 为直径，有 \(\angle PAI=\angle DAS=\angle NST\)

又 \(PA=PI=>\angle PAI=\angle PIA\)

有 \(\angle PIA=\angle NST\)

即 \(\angle MST+\angle IMS=\pi\)

即 \(ST//MI\)

而 \(MI//SK\iff \frac{MS}{NS}=\frac{IK}{NK} \iff R^2-OI^2=2Rr\) 成立

即证。

例4

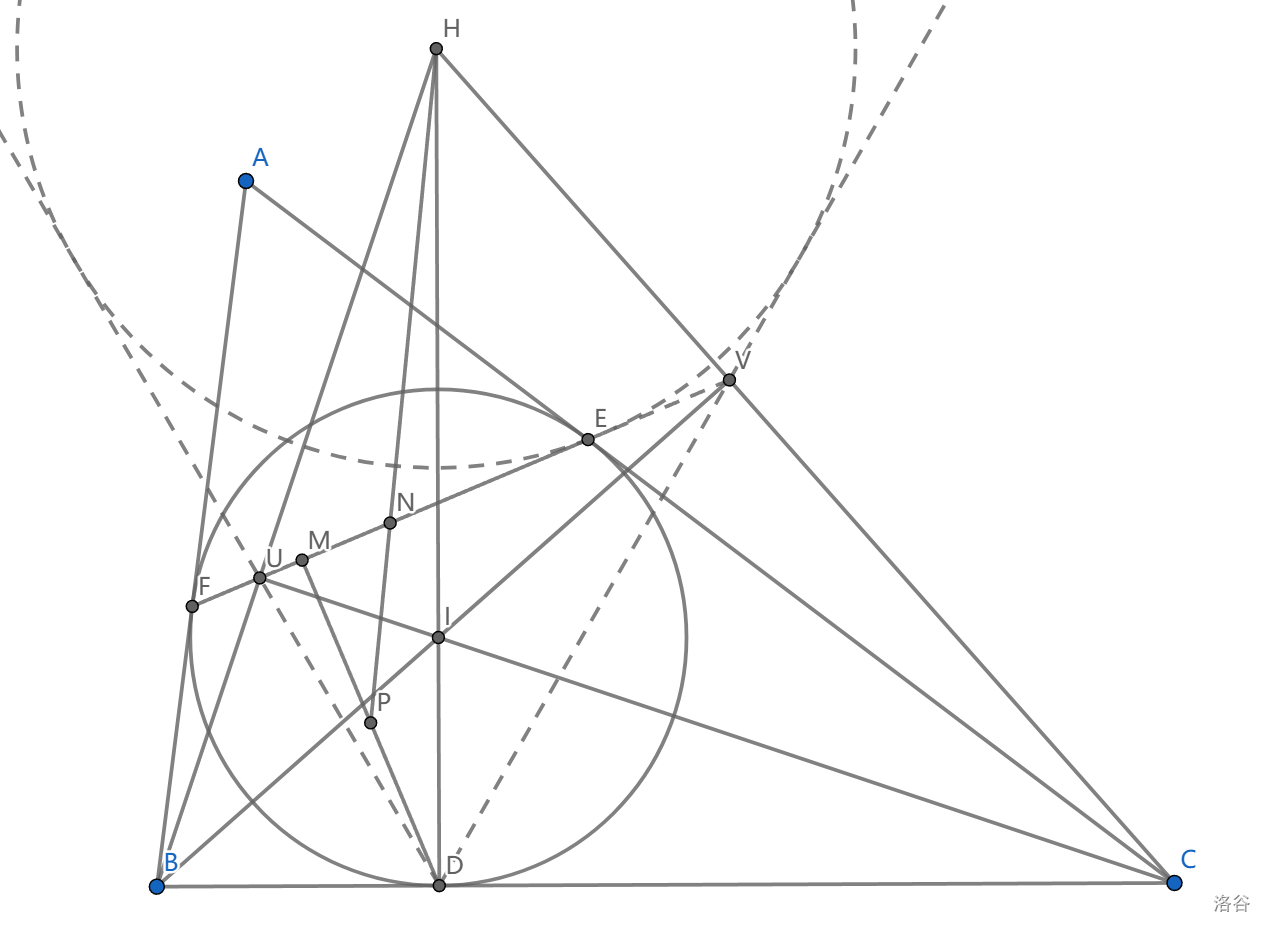
如图，\(\triangle ABC\) 的内心为 \(I\) ，切触三角形为 \(\triangle DEF\) ， \(M\) 是 \(D\) 到 \(EF\) 的投影， \(P\) 是 \(DM\) 的中点， \(H\) 是 \(\triangle BIC\) 的垂心，证明： \(PH\) 平分 \(EF\)

有了一个垂心，我们先可以构造 \(B\) 到 \(CI\) 的垂足 \(U\) 和 \(C\) 到 \(BI\) 的垂足 \(V\) ，根据性质 \(12\) ， \(UVEF\) 共线。

因为 \(I\) 是 \(\triangle BHC\) 的垂心，所以它是 \(\triangle DUV\) 的内心，因此 \(EF\) 的中点 \(N\) 是它的内切圆切点。于是我们看到了性质 \(6\) 的构型，我们只要证明 \(H\) 是 \(\triangle DUV\) 的旁心

这是非常熟知的事实，实际上， \(\angle HVU=\angle CVD=C\) ，所以 \(VH\) 是 \(\angle DVU\) 的外角平分线，另一边也是如此。

例5

\(\triangle ABC\) 中，\(A,B,C-\) 旁切圆切点为 \(D,E,F\) ，证明这三线共点；设为 \(N\) ，设 \(BE,CF\) 与内切圆交于 \(P,Q\) ，证明： \(S_{\triangle NBC}=S_{PQEF}\)

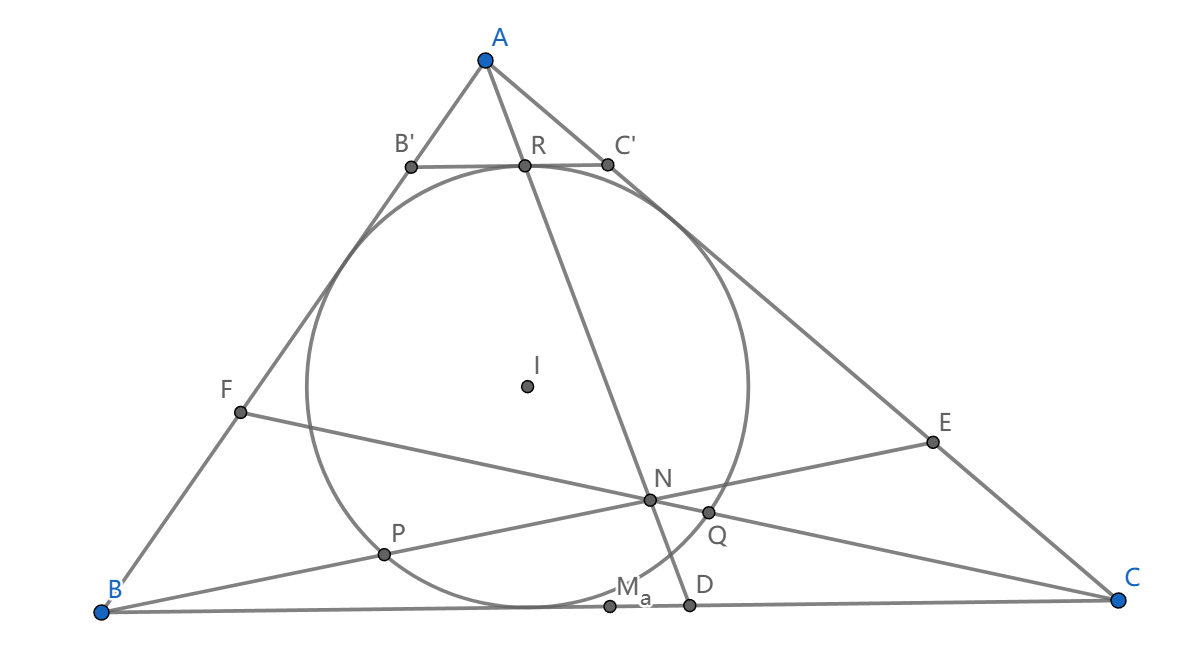
这个点被称为 \(Nagel\) 点。它有很多有趣的性质，比如是内切圆与外切圆位似中心的等角共轭点，我们用位似证明它的存在。

注意到 \(\triangle AB'C'(R')\sim\triangle ABC(D)\) ，并且 \(AR//M_aI\) （中位线），所以 \(AD,BE,CF\) 共点 \(N\) 相当于中点三角形 \(M_aM_bM_c\) 中的 \(I\)

现在可以计算面积。 \(S_{PQEF}=\frac 12\cdot PE\cdot QF\cdot \sin \angle FNP,S_{NBC}=\frac 12 NB\cdot NC\cdot \sin\angle BNC\) ，要证明 \(PE\cdot QF=NB\cdot NC\)

我们注意到根据位似关系 \(NB=2IM_c\) ，其中 \(I,M_c\) 分别是 \(QT,TF\) 的中点（ \(T\) 是内切圆切点），\(NB=QF\) ，这就证毕

例6

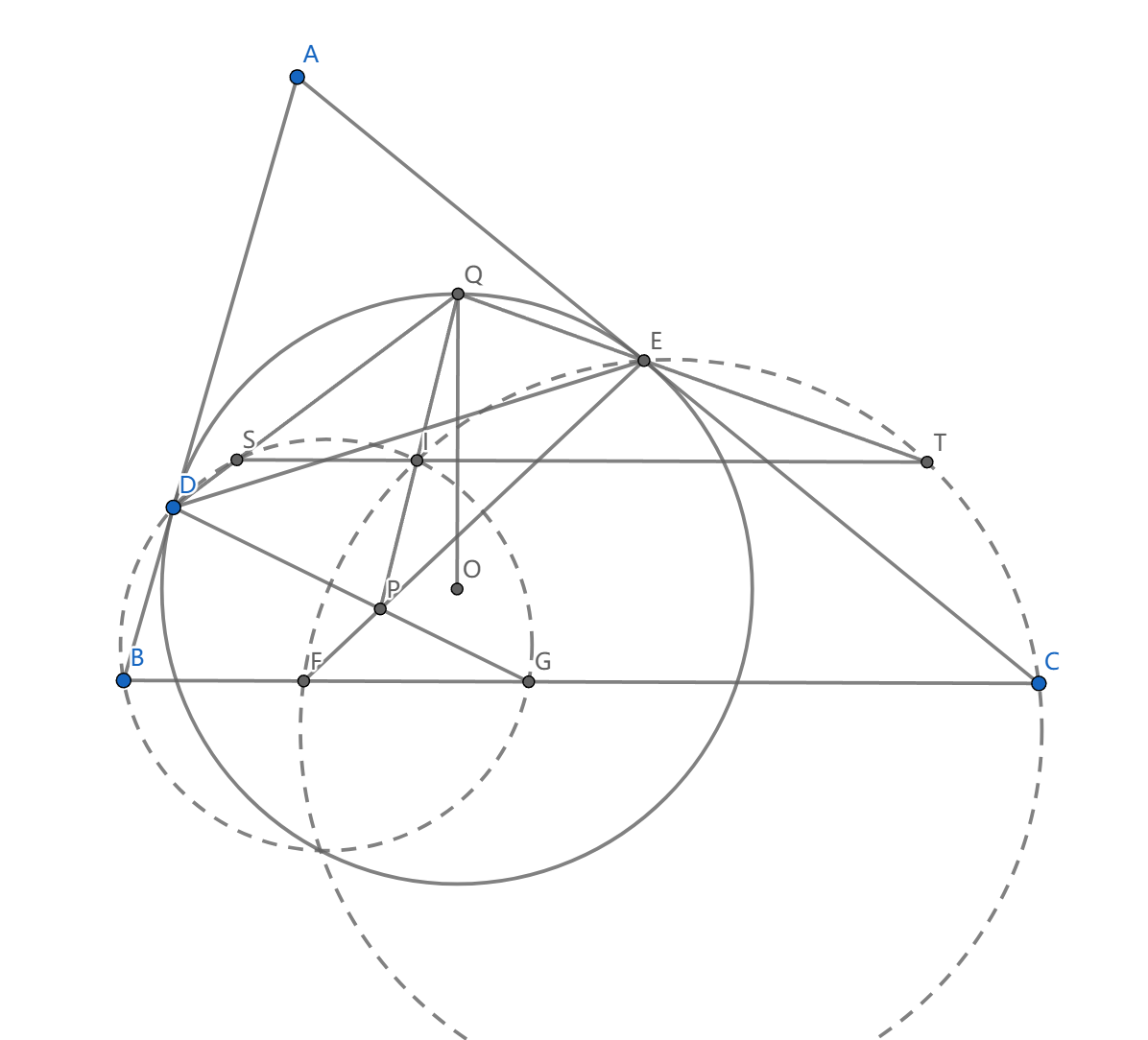
如图， \(\odot O\) 切 \(AB,AC\) 于 \(D,E\) ， \(BF=BD,CG=CE\) ， \(P=EF\cap DG\) ， \(OQ\perp BC\) ， \(I\) 是内心，求证： \(PIQ\) 共线

这个构型与伪内切圆还是很像的，我们可以尝试找一些共圆。首先注意到的是 \(ID=IE\) ，同时 \(BI\) 是角平分线，三线合一，然后 \(ID=IF,IE=IG\) ，所以 \(DEGF\) 共圆

根据对称性，还有 \(\angle IGF=\angle IEA=\angle IDA=\angle IFG\) ，所以 \(BDIG,CEIF\) 共圆。用根心定理，我们看到 \(P\) 是根心，从而 \(IP\) 是这两个圆的根轴。

我们来证明 \(Q\) 在这条根轴上，没什么好的方法，只能导圆幂。我们设 \(QD\cap (BDIG)=S,QE\cap (CEIF)=T\)

我们先导 \(\angle QDE\) ，实际上因为 \(OQ\perp BC,EO\perp AD\) ，我们有 \(\angle QOE=C\) ，所以 \(\angle QDE=\frac 12C\) ，同理 \(\angle QED=\frac 12 B\)

我们再用共圆导角，看到 \(\angle QSI=\angle DBI=\frac 12B,\angle QTI=\frac 12C\) ，所以 \(\angle QSI+\angle QTI+\angle SQT=\pi\) 给出 \(SIT\) 共线， \(\triangle QDE\sim\triangle QTS\) ，看到 \(QD\cdot QS=QE\cdot QT\) ，这就证毕。

伪内切圆

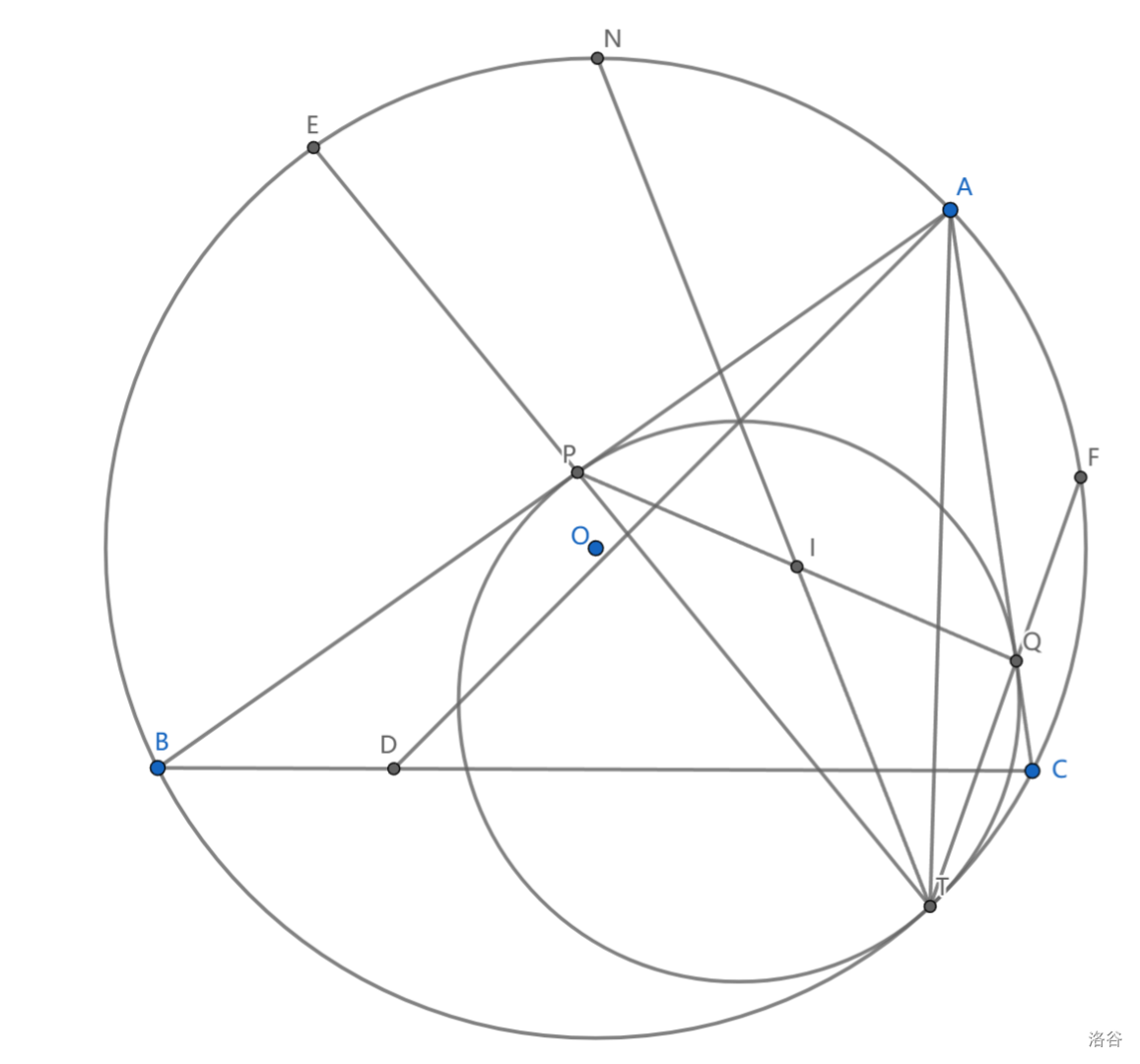
\(\triangle ABC\) 的伪内切圆是指一个与它的两边相切并且与它的外接圆内切的圆，如图展示的是一个 \(A-\) 伪内切圆。

设与外接圆切点为 \(T\) ，与边 \(AB,AC\) 切于 \(P,Q\) ， \(I\) 为内心， \(N\) 为弧 \(BAC\) 中点，则

1. \(I\) 为 \(PQ\) 中点

2. 直线 \(TP,TQ\) 经过弧 \(AB,AC\) 的中点

3. \(BITP,CITQ\) 共圆（这两个四边形还是相似的，可以参见圆幂笔记中的构型，进一步还能给出 \(\frac{BT}{CT}=(\frac{BI}{CI})^2\)）

4. \(NIT\) 共线

5. \(A-\) 旁切圆切点 \(D\) 满足 \(\angle BAD=\angle CAT\)

6. 内切圆切点 \(S\) 满足 \(\angle BTA=\angle CTS\)

7. \(\triangle AID\sim \triangle ATI_A\)

两圆关于点 \(T\) 位似

1. 考虑点 \(P\) 位似对应点 \(E\) ，它们关于两圆切线应平行，那么可知 \(E\) 就是弧 \(AB\) 中点，同理 \(F\) 是弧 \(AC\) 中点

对圆内接六边形 \(ABFTEC\) 用 \(Pascal\) 定理，知 \(PIQ\) 共线

很显然伪内切圆的圆心在 \(AI\) 上，这意味着 \(AP=AQ\) ，从而 \(IP=IQ\)

注：如果 \(D\) 是 \(AB\) 上一点，圆 \(\omega\) 与 \(CD,BD,\odot(ABC)\) 相切于 \(P,Q\) ，那么 \(PQ\cap CE=I\) 是 \(\triangle ABC\) 的内心。

证明思路不太一致，还是有 \(CQIT\) 共圆，然后给出 \(\triangle EPI\sim \triangle EIT\) ，这是弧中点性质+鸡爪定理的相似，所以 \(I\) 是内心。

4. \(\angle BIP=\angle BIA-Rt\angle=\frac 12C=\angle BTE=\angle BTP\) ，从而 \(BITP\) 共圆，从而 \(\angle ETI=\angle EBI=\frac 12 B=\angle ETN\) ，即证

5. 以 \(A\) 为反演中心， \(AB\cdot AC\) 为幂作反演，则伪内切圆变为旁切圆（因为弧 \(BC\) 变为线段， \(T\) 到了线段 \(BC\) 上），那么 \(T\) 对应点就是 \(\triangle AB'C'\) 旁切圆切点 \(T'\) ，则 \(\angle CAT=\angle C'AT'=\angle BAD\)

6. 延长 \(AD\) ，我们看到一个等腰梯形，于是延长 \(TD\) 交外接圆，我们会看到这是一个对称的图形。

还可以在伊朗式反演下找到伪内切圆的一些处理手法。

例1

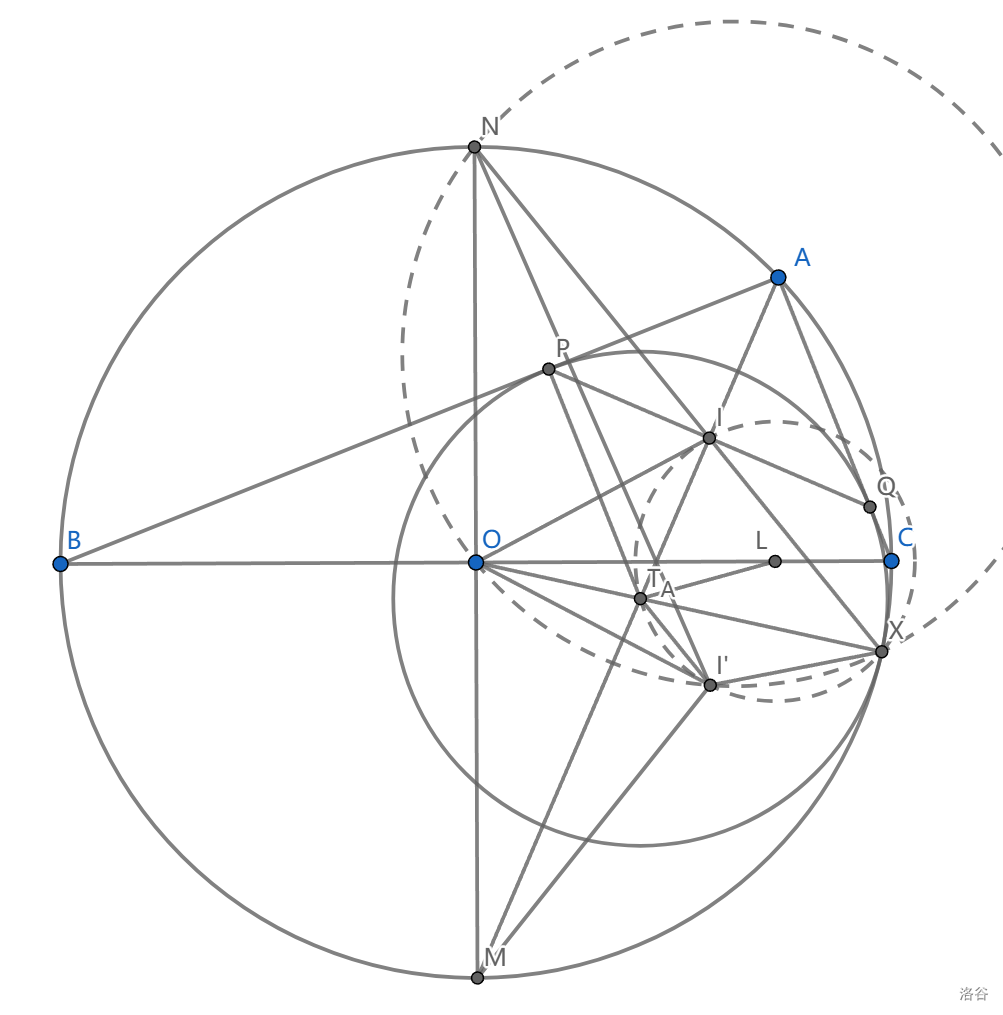
如图， \(Rt\triangle ABC\) 内接于圆 \(O\) ， \(I\) 是内心， \(X\) 是 \(A-\) 伪内切圆 \(\odot T_A\) 切点，过 \(T_A\) 做 \(AX\) 垂线交 \(BC\) 于点 \(L\) ，求证： \(L\) 是 \(\odot IXT_A\) 外心。

画一个好的图，很快就发现 \(AX\) 就是 \(\odot L\) 与 \(\odot T_A\) 的根轴。这个说明不困难，因为 \(\angle APT_A=Rt\angle\) ，直接用射影定理有 \(AP^2=AI\cdot AT_A\) ，所以 \(A\) 在根轴上

于是我们只要 \(L\in BC\) ，不难想到要取对称点证明共圆。我们可能会构造根轴 \(XY\) ，但这是不好的，我们应当取 \(I\) 关于 \(BC\) 的对称点 \(I'\) ，不难看出后者明显更优秀一些

接下来的证明比较困难。 \(IT_AI'X\) 并不是很容易导角或者导圆幂，我们只能先退而看看我们拥有什么条件了。

我们还没有利用伪内切圆的一些性质，比如说 \(XIN,XT_AO,AIT_AM\) 分别共线。一个非常不容易的观察是， \(I'\) 在 \(\triangle XIT_A,\triangle MNI\) 的外接圆上，它是四边形 \(INOT_A\) 的密克点！

于是只要证明 \(XI'ON\) 共圆。这个共圆可以利用内心的性质 \(11\) 轻松证明，我们有 \(\angle NI'O=\angle I'MO\overset{对称}{=}\angle INO=\angle OXN\) ，已经有 \(MNII'\) 共圆，这就证毕。

例2

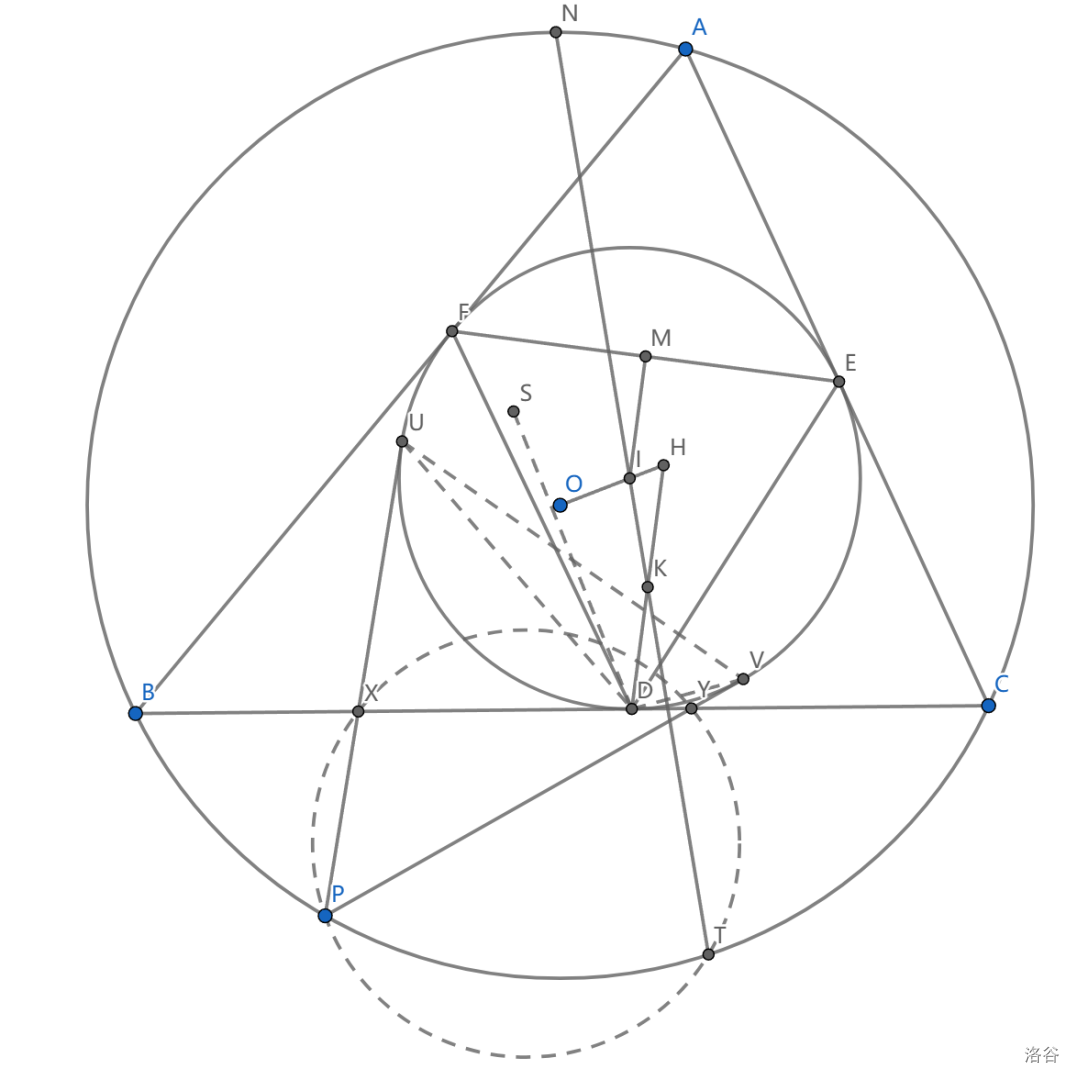
如图， \(P\) 是弧 \(BC\) 上一动点，过 \(P\) 做内切圆 \(\odot I\) 切线交 \(BC\) 于 \(X,Y\) ， \(T\) 是 \(A-\) 伪内切圆切点，证明： \(PXYT\) 共圆。

这题有很多有意思的纯几何做法，但最自然的应当是反演做法，关于内切圆反演。

\(X,Y,P\) 对应了 \(DU,DV,UV\) 的中点，这些是平凡的，但我们要证明一下 \(T\) 对应的是 \(DH\) 中点， \(H\) 是 \(\triangle DEF\) 的垂心。

这并不很困难，首先 \(NI//MH\) ，因为它们是切触三角形与旁心三角形位似对应点，然后用熟知的平行四边形 \(MIKH\) ，我们就知道 \(NIKT\) 共线。

然后 \(T\) 在 \(\triangle ABC\) 的外接圆上，于是反演后在 \(\triangle DEF\) 的九点圆上，于是它对应 \(K\) 。

现在关于 \(D\) 做一次位似，把四个中点变成了 \(U,V,K,S\) ，然后再关于 \(UV\) 中点做一次对称，我们说 \(H\) 关于 \(UV\) 中点的对称点在 \(\odot I\) 上，其余三个点明显是这样的，我们来证明这一点。

实际上， \(UV\) 的中点是 \(P\) 的对应点，所以它在 \(\triangle DEF\) 九点圆上，而九点圆与外接圆位似中心为 \(H\) ，这就证毕。

注：1. 利用切触三角形与旁心三角形的位似，我们可以证明 \(OIH\) 共线（考虑两个三角形的欧拉线即可），这也是一个常用的性质。

2. 我们可以直接证 \(K\) 在 \(\triangle DUV\) 的九点圆上。实际上 \(K\) 是四边形 \(DUHV\) 的 \(Poncelet\) 点（四个三角形的九点圆交点）

多内心问题

偶尔会有一些问题涉及了多个三角形的内心。

例1

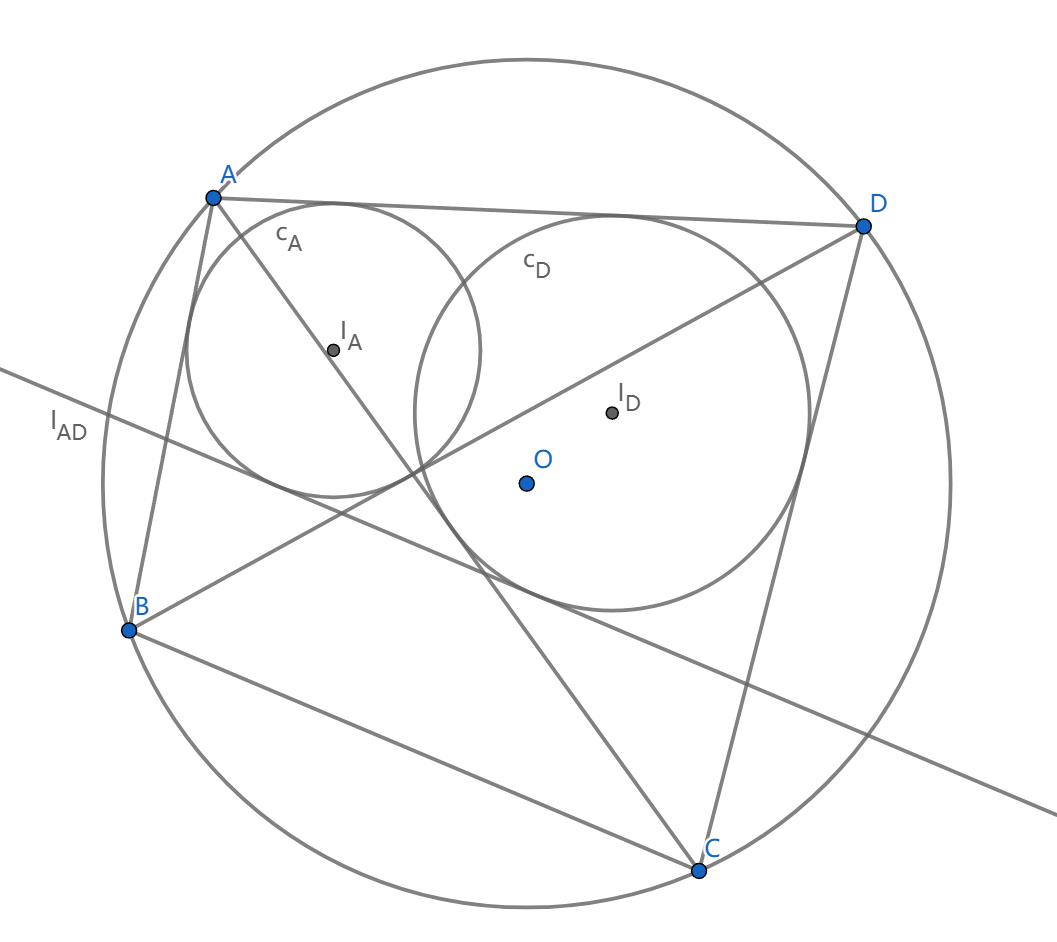
四边形 \(ABCD\) 内接于圆， \(c_A,c_B,c_C,c_D\) 分别是 \(\triangle DAB,\triangle ABC,\triangle BCD,\triangle CDA\) 的内切圆， \(c_A,c_B\) 的一条外公切线（不同于 \(AB\) ）是 \(l_{AB}\) ，类似定义 \(l_{BC},l_{CD},l_{DA}\) ， \(X=l_{AB}\cap l_{DA},Y=l_{BC}\cap l_{CD}\) ，证明： \(AX//CY\)

我们在圆幂与根轴谈论过这样的一个构型，我复制粘贴到了这里。

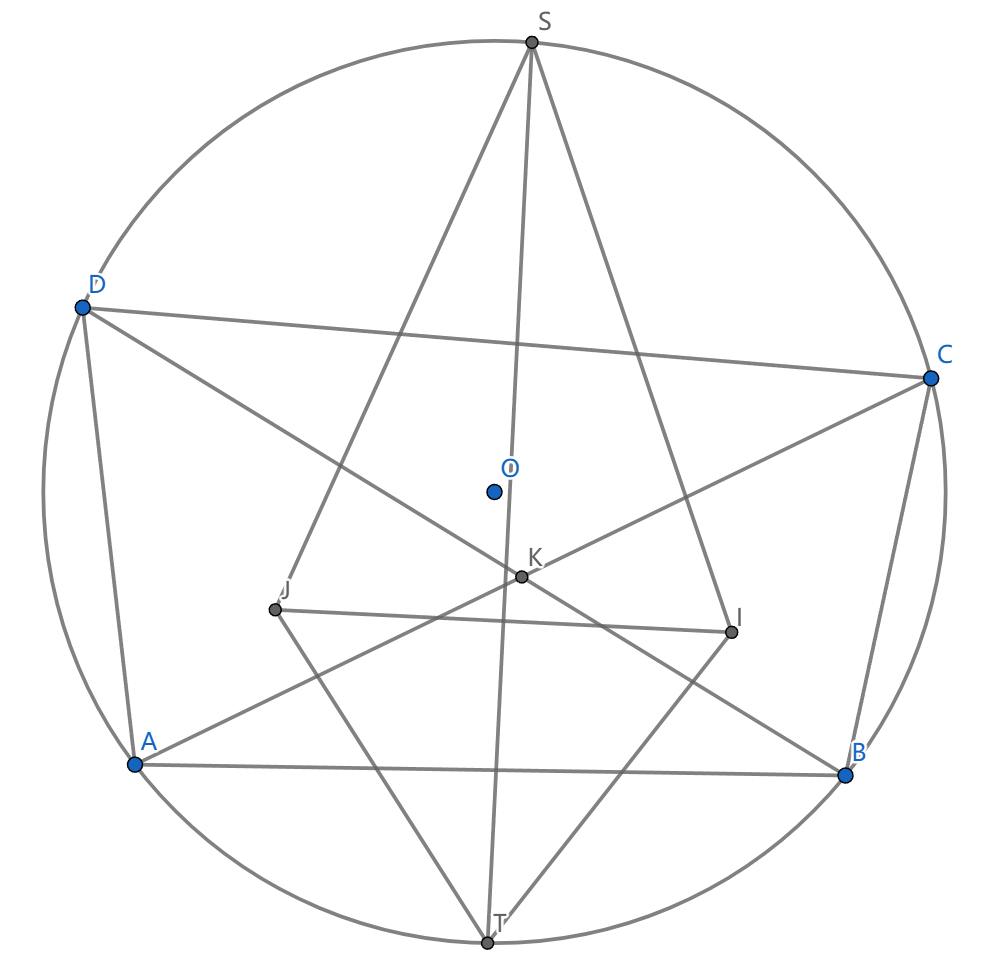
如图，根据鸡爪定理，我们看到 \(SI=SC=SJ,TI=TB=TJ\) ，从而 \(ST\perp IJ\) ，而 \(\angle AKB\) 的平分线平行于 \(ST\)

然后取出另外两个弧中点连线，与 \(ST\) 垂直，于是可以得到矩形 \(I_AI_BI_CI_D\)

不过这个问题用不到。因为 \(I_AI_B//ST\) 实际上平行于 \(\angle AKB\) 角平分线，导致 \(c_A,c_B\) 的另一条公切线实际上 \(//CD\) 。

所以 \(l_{AB},l_{AD}\) 和 \(AD,AB\) 围成的四边形与 \(l_{CB},l_{CD},CD,CB\) 围成的四边形对应边两两平行，他们位似，就有 \(AX//CY\)

例2

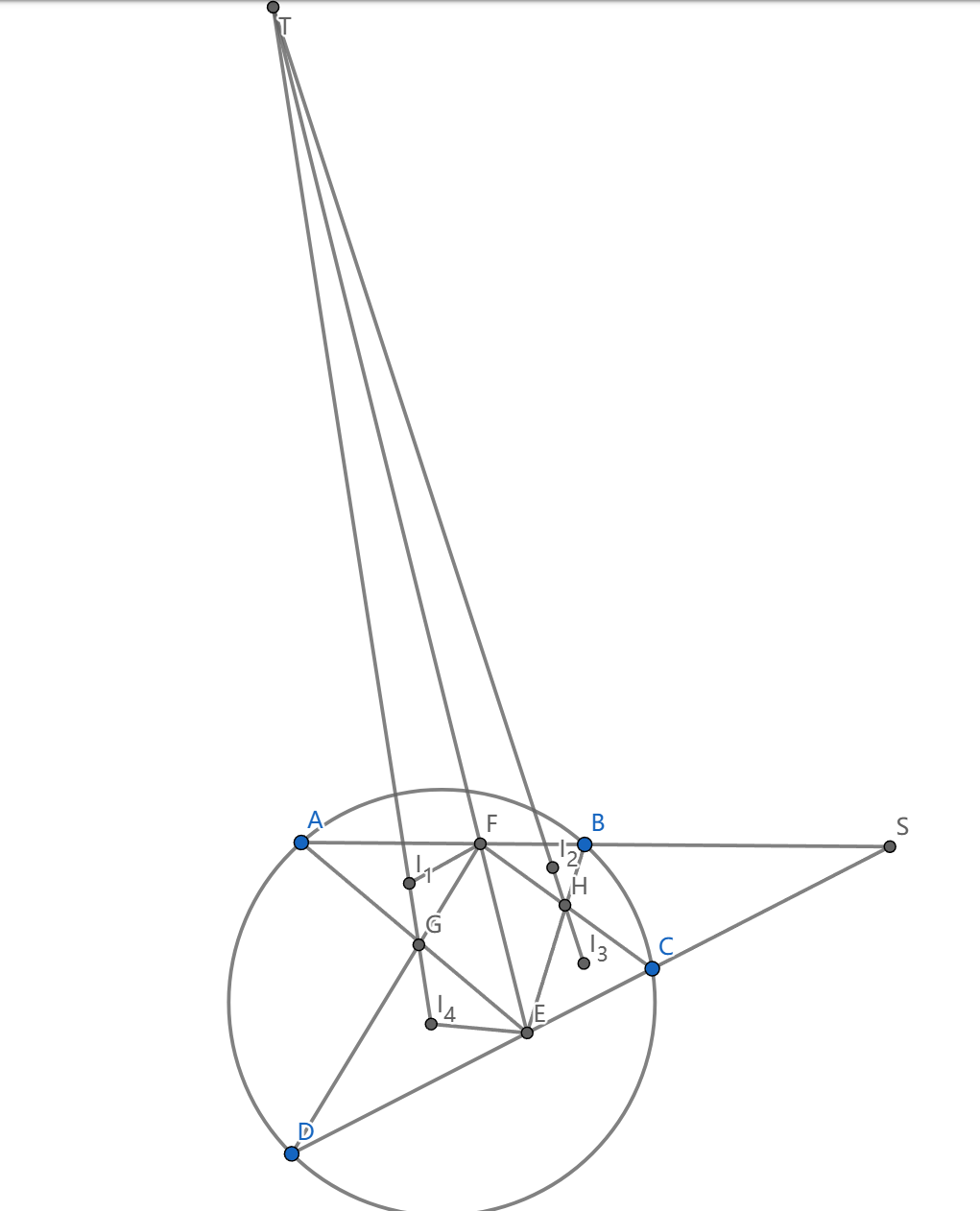
圆内接四边形 \(ABCD\) 中，过 \(A,B\) 的圆与 \(CD\) 切于 \(E\) ，过 \(C,D\) 的圆与 \(AB\) 切于 \(F\) ，\(G=AE\cap DF,H=BE\cap CF\) ，求证： \(\triangle AGF,BHG,CHE,DGE\) 的内心共圆。

失去了鸡爪定理的构型，我们比较难刻画内心的连线，导角不太可行，而导圆幂看上去也很困难。做一个好的图也许会给出提示，我们发现 \(I_1I_4,I_2I_3,EF\) 是共点的。

我们先利用相切的条件，看到 \(SE^2=SA\cdot SB=SC\cdot SD=SF^2\) ，我们可以导角得到（用弦切角）

\(\angle DFE=\angle SFD-\angle SFE=\angle SCF-\angle SEF=\angle CFE\)

同理 \(EF\) 也平分 \(\angle AEB\) ，那么 \(\triangle EFG\cong \triangle EFH\) ，而 \(I_1I_4,I_2I_3\) 是它们的外角平分线，全等说明它们与 \(EF\) 交于一点 \(T\)

现在我们只要证明 \(I_1I_4EF\) 共圆。这个导角不困难

\(\angle FI_1I_4=Rt\angle +\frac 12\angle GAF\overset{弦切角}{=}Rt\angle +\angle BES=\pi-\frac 12\angle BED=\pi-\frac 12(\angle BEA+\angle GED)=\pi-\angle FEI_4\)

然后 \(TI_1\cdot TI_4=TF\cdot TE=TI_2\cdot TI_3\) ，证毕。