外心与垂心

外心

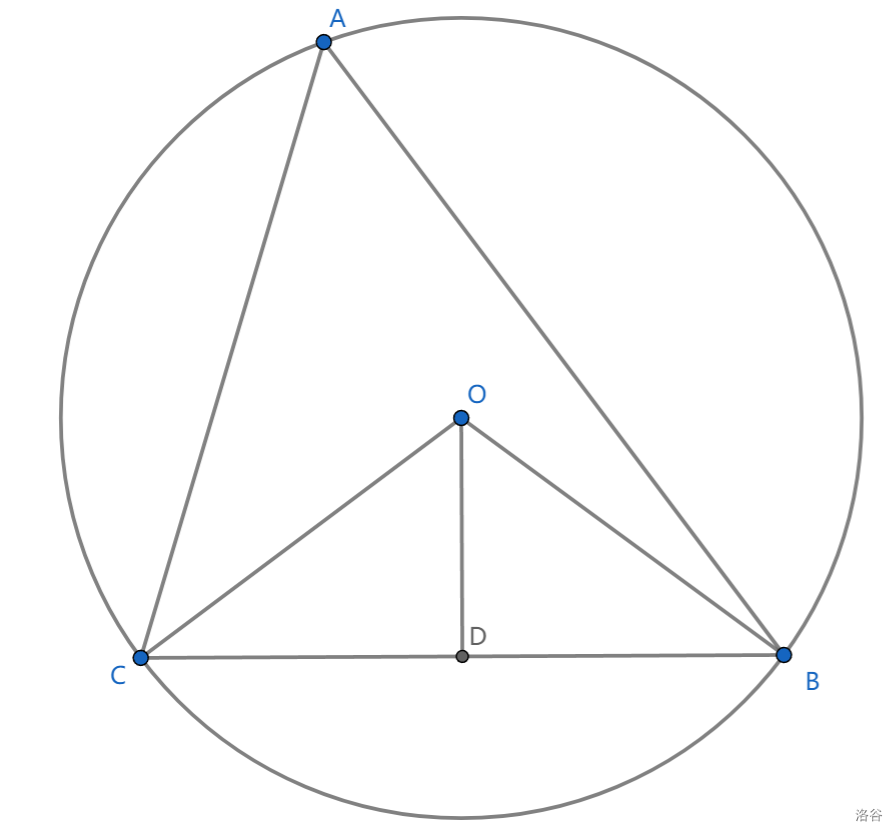
（这三条结论并不完全是平凡的）

1、 \(\angle BOC=2\angle A\)

2、 \(\angle CBO+\angle A=Rt \angle\)

3、 \(O\) 在三角形三边的中垂线上

例1

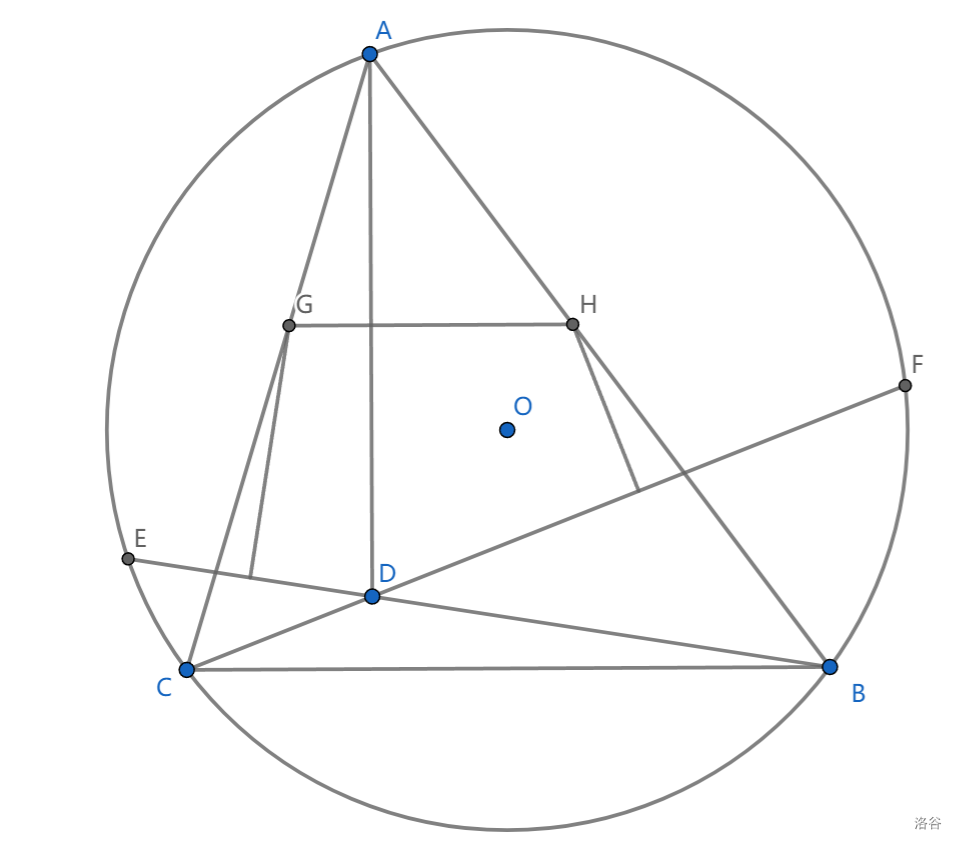
如图，\(\triangle ABC\) 内接于圆 \(O\) ，\(AD\perp BC\) ，延长 \(CD,BD\) 交圆 \(O\) 于点 \(F,E\) ，作 \(DE,DF\) 中垂线交 \(AC,AB\) 于点 \(G,H\) ，证明 \(GH // BC\)

分析：注意到 \(GH\) 似乎是 \(AD\) 的中垂线，猜测 \(G,H\) 为外心

考虑外心的刻画。在这里，最适合的是使用性质2，即 \(\angle DAH+\angle AFD=Rt\angle\) ，这里恰好不会用到点 \(H\) ，从而可证 \(G,H\) 为外心

例2

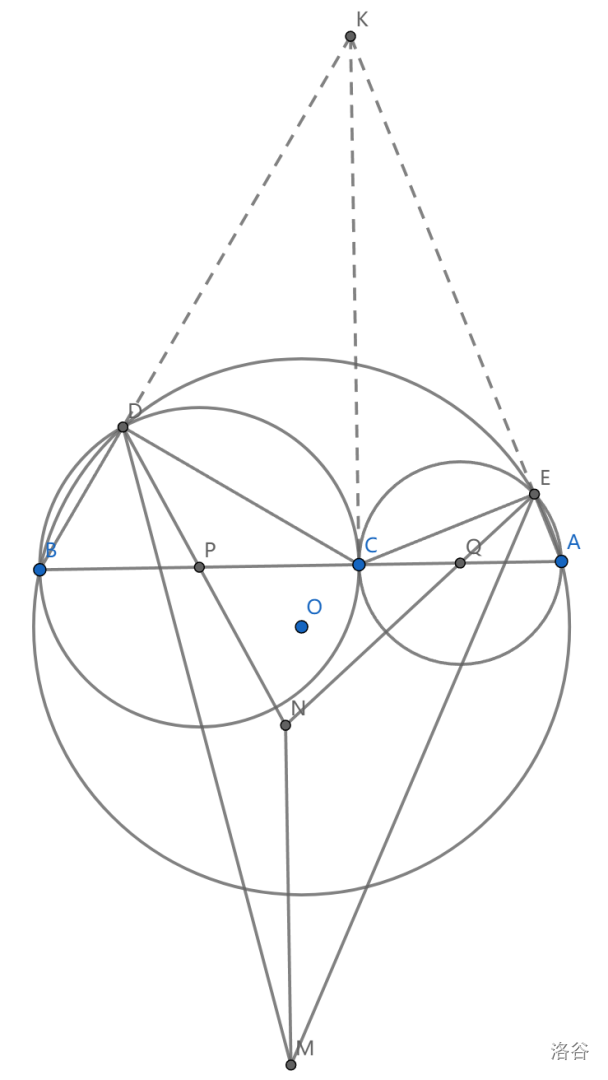
如图，\(AB\) 为圆 \(O\) 的弦，\(C\) 在 \(AB\) 上， \(D,E\) 在圆 \(O\) 上且满足 \(\angle BDC=\angle AEC=Rt\angle\) ， \(P,Q\) 为 \(BC,AC\) 中点，延长 \(DP,EQ\) 交于点 \(N\) ， \(\angle BDC\) 与 \(\angle AEC\) 的内角平分线交于点 \(M\) ，证明： \(MN\perp AB\)

首先由三个圆不难联想到构造根心，得到点 \(K\) ，有 \(CK\perp AB\) 及 \(K,E,C,D\) 共圆

同时可以注意到 \(NE=ND\) ，因为 \(\angle NDE=\angle CDN+\angle CDE=\angle CKB+\angle CKE=\angle AKB\) ， \(\angle NED\) 同理

事实上， \(\angle EMD=\angle END-(\angle NEM+\angle NDM)\) ，不难得到其与 \(\angle NEF\) 互余，即 \(N\) 为 \(EFM\) 外心

然后随便导角都可以出来

例3

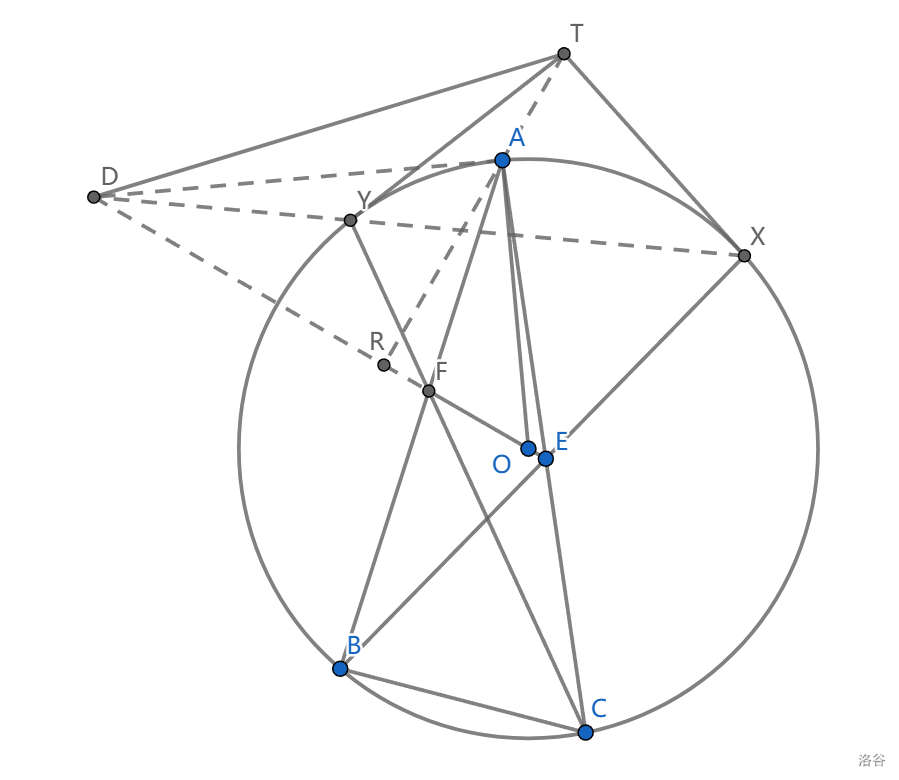
如图， \(E,F\) 是 \(AB,AC\) 上两点， \(O\) 在 \(EF\) 上，延长 \(BE,CF\) 交外接圆于 \(X,Y\) ，过 \(X,Y\) 做外接圆的切线交于点 \(T\) 。求证： \(TA\perp EF\)

首先，这道题的 \(Pascal\) 构型并不难看出。定义 \(D=AA\cap XY\) ，我们可以对 \(AABXYC\) 用 \(Pascal\) ，看到 \(D\) 在 \(EF\) 上。

看到这样的构型，我们应当做一些圆幂计算。要做圆幂计算，我们可以先将 \(AR\perp EF\) 做出来，已经有 \(AO\perp AD\) ，借助射影定理可以得到更多不错的条件（这个技巧再常见不过了）。

我们看到 \(DR\cdot DO=DA^2=DY\cdot DX\) ，所以 \(ORYX\) 共圆，而且 \(T\) 在这个圆上，很不错， \(OT\) 是直径，从而 \(\angle ORT=Rt\angle =\angle ORA\) ，这就完成了证明。

例4

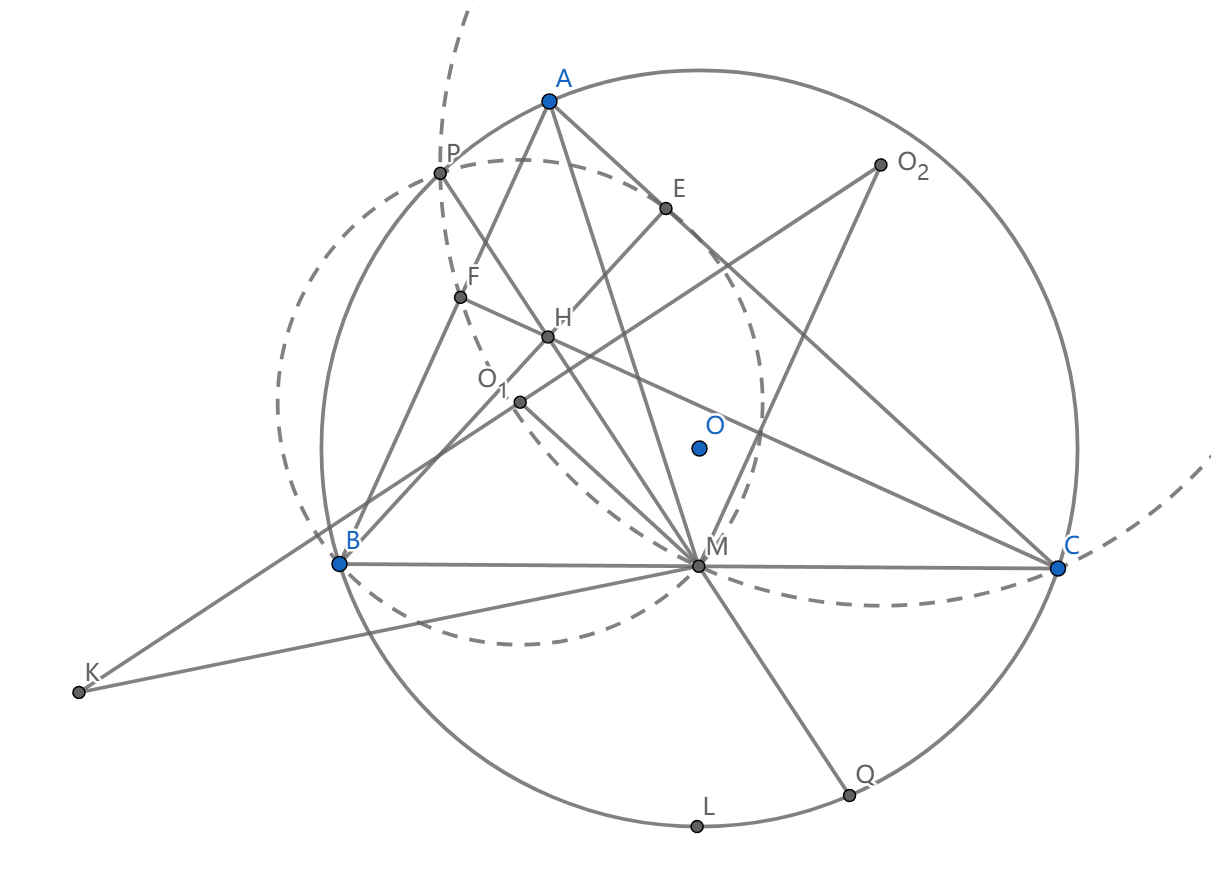
如图， \(\triangle ABC\) 中， \(BE,CF\) 为高， \(M\) 为 \(BC\) 中点， \(L\) 为弧 \(BC\) 中点， \(K\) 是 \((BME)\) 和 \((CMF)\) 的外位似中心，求证： \(KM=KL\)

画一个好的图，然后看到 \((BME),(CMF),(ABC)\) 是共点的。我们设 \(P=(BME)\cap(CMF)\) ，然后证明 \(P\) 在 \((ABC)\) 上

我们要求 \(\angle BPC\) ，利用根轴将这个角割开，我们看到 \(\angle BPC=\angle BPM+\angle CPM=\angle BEM+\angle CFM=\frac{\pi}2-B+\frac{\pi}2-C=A\) （最后一步用到 \((BFEC)\) 的圆心是 \(M\) ），所以 \(APBC\) 共圆。

上面的中间结论给出 \(\angle BPM=\frac{\pi}2-B=\frac{\pi}2-\overset{\frown}{AB}\) ，延长 \(PM\) 交 \((ABC)\) 于 \(Q\) ，就会有 \(AQ\) 是直径

我们要取出两个外心 \(O_1,O_2\) 来利用位似条件。我们知道 \(O_1O_2\) 垂直平分 \(PM\) ，而 \(K\) 在这条垂直平分线上，所以我们要证的结论就变为 \(K\) 是 \(PML\) 的外心

这很不错，我们可以把问题变为一个导角。在此之前我们需要继续刻画 \(O_1,O_2\)

我们看到 \(MO_2\perp CF\) （准确地说是垂直平分），所以 \(MO_2//AB,MO_1//AC\)

并且 \(\frac{KO_1}{KO_2}=\frac{r_1}{r_2}=\frac{MO_1}{MO_2}\) ，说明 \(MK\) 是 \(\angle O_1MO_2\) 的外角平分线（实际上外位似中心和内位似中心和两圆心有个调和点列，所以说这个角平分线是应该记住的）

我们的重要结论是说 \(\angle O_1MO_2\) 与 \(\angle BAC\) 是位似的，所以 \(MK\) 将会垂直 \(\angle BAC\) 的平分线即 \(AL\) 。至此问题基本解决，我们看到：

\(\angle KMP=\frac{\pi}2-<AL,PM>=\frac{\pi}2-(\overset{\frown}{AP}+\overset{\frown}{LQ})=\overset{\frown}{PQ}=\frac{\pi}2-\angle PLM\)

证毕。

垂心

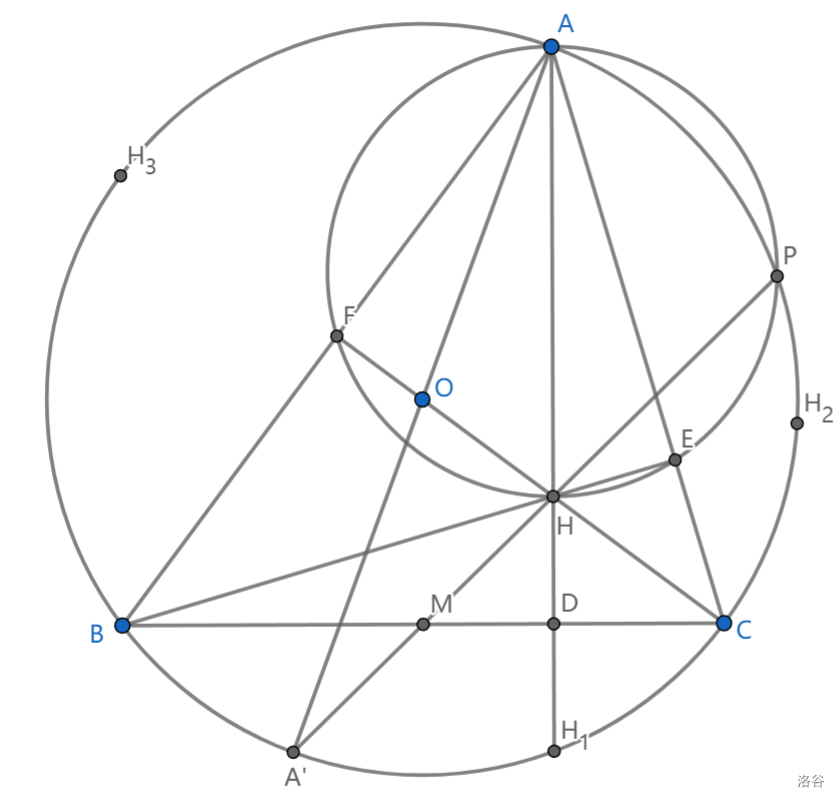
1、\(H\) 为 \(\triangle DEF\) 内心

2、（鸭爪定理）\(H\) 关于三边对称点在外接圆上

3、\(AH\cdot HD=BH\cdot HE=CH\cdot HF\) （可用于反演）

4、\(\triangle ABC,\triangle BCH\) 等三角形的外接圆半径相等

5、\(AH=2OM\) ，其中 \(\angle BAO=\angle CAH\)

6、\(MH\) 与外接圆交点 \(A',P\) 满足 \(A'\) 为 \(A\) 对径点且 \(A'M=MH\)，\(AFHEP\) 共圆

7、\(O,H\) 为等角共轭点

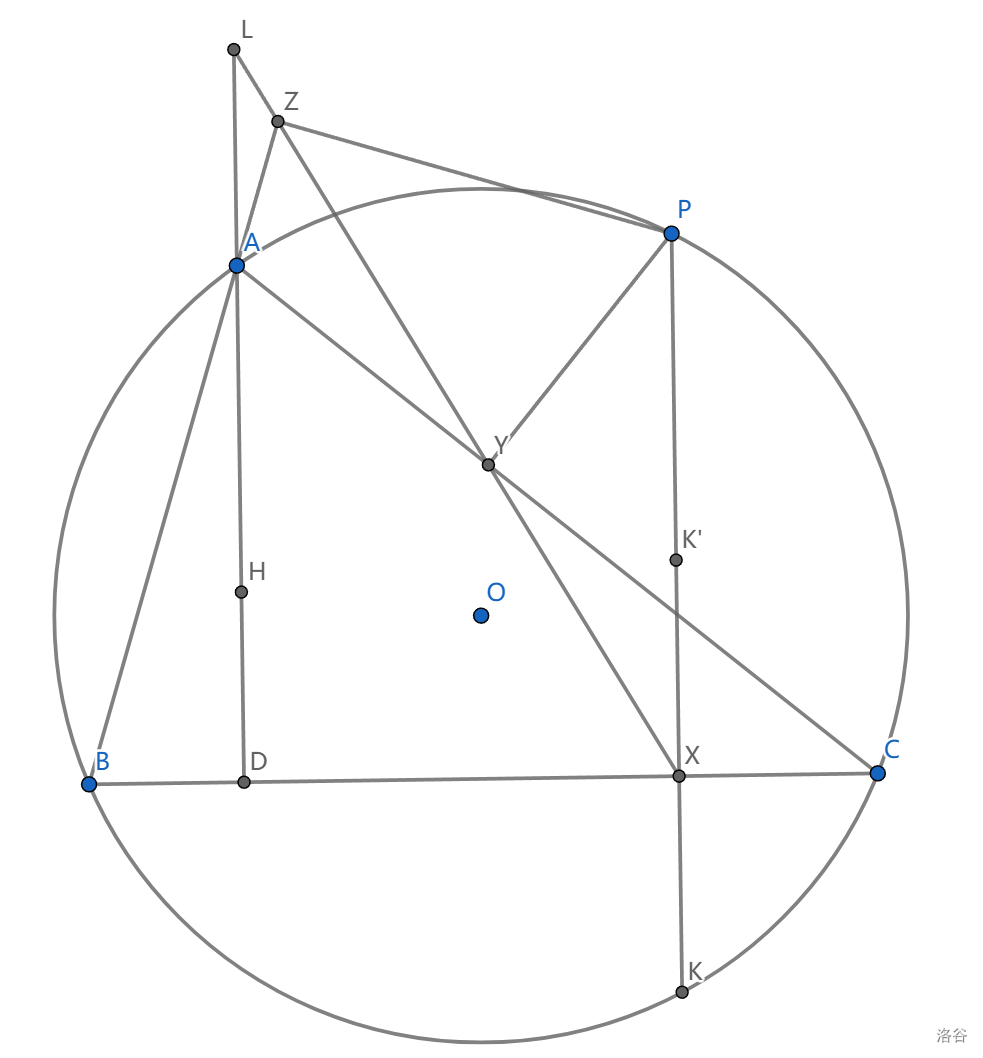
8、对弧 \(BC\) 上任一点 \(P\) ， \(PH\) 平分点 \(P\) 关于 \(\triangle ABC\) 的西姆松线

这个结论的证明需要引理（其实可以不用，但是我们想发掘这个构型的更多性质：

9、圆内接四边形 \(ABCD\) 中， \(X,Y\) 分别是 \(\triangle ABC,\triangle BCD\) 的垂心，则 \(AXYD\) 是平行四边形

这个可以用鸭爪定理得到一个等腰梯形后轻松证明。

我们说 \(K\) 关于 \(BC\) 的对称点 \(K'\) 是 \(\triangle PBC\) 的垂心，即鸭爪定理的逆定理（最好说是导角），所以 \(AHK'P\) 是平行四边形

西姆松线上显然有 \(PXYC\) 共圆，用 \(Reim\) 引理可以看到 \(AK//LX\) ，同时 \(LA//XK\) ，所以有平行四边形 \(ALXK\) ，则 \(AL=XK=XK'\)

结合两个条件可知 \(LH=XP,LH//XP\) ，完成了证明。

例1

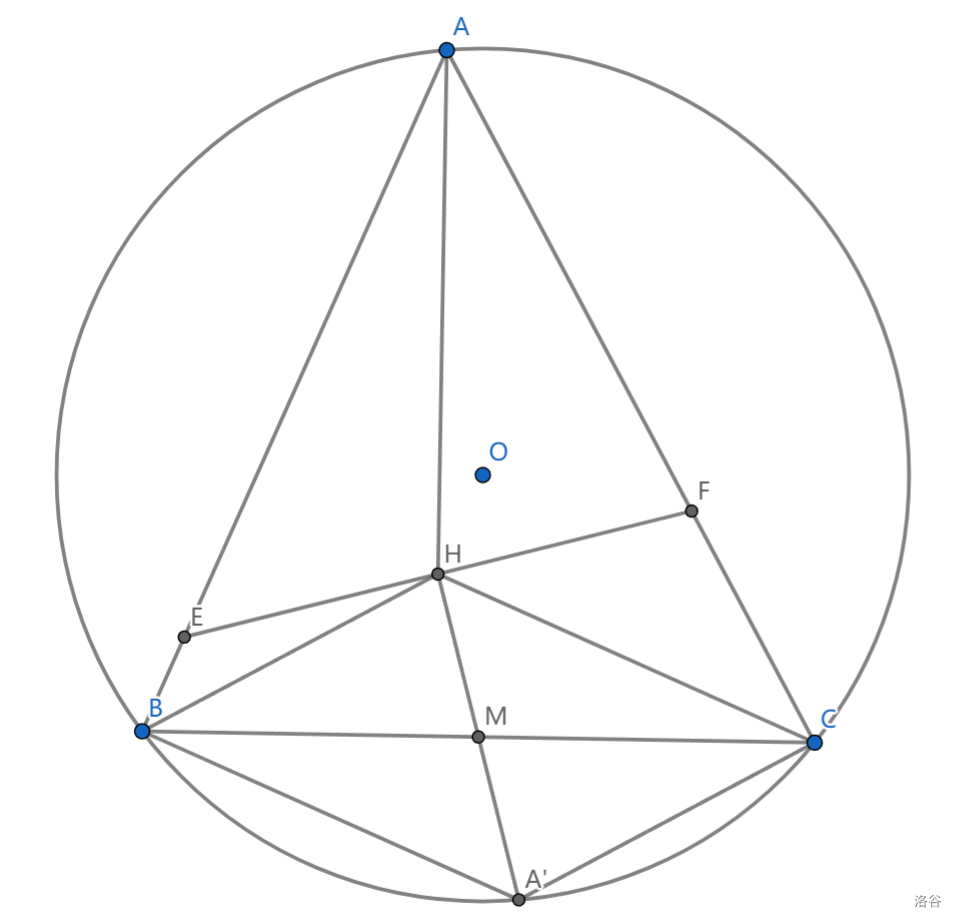
如图，\(M\)为 \(BC\) 中点， \(EF\perp HM\) ，求证：\(EH=HF\)

这个构型比较常见，实际上可以证明 \(\frac{EH}{FH}=\frac{BM}{CM}\)

\(\angle MCH=\angle HAE\)

又 \(AE\perp CH,HM\perp EF\) ，可知\(\angle AEH=\angle CHM\)

从而 \(\triangle AEH\sim \triangle CHM\)

同理 \(\triangle AFH\sim \triangle BHM\)

接下来利用垂心的性质，还能看到很明显的全等 \(\triangle BHM\overset{\backsim}{=} \triangle CA'M\) ，可知 \(\triangle CA'H\sim\triangle AFE\)

那么就有 \(CFHA'\) 共圆，同理 \(BEHA'\) 共圆

可知 \(\angle HFA'=\angle HCA'=\angle HBA'=\angle HEA'\)

即 \(A'H\) 为 \(EF\) 中垂线，这就做完了。

例2

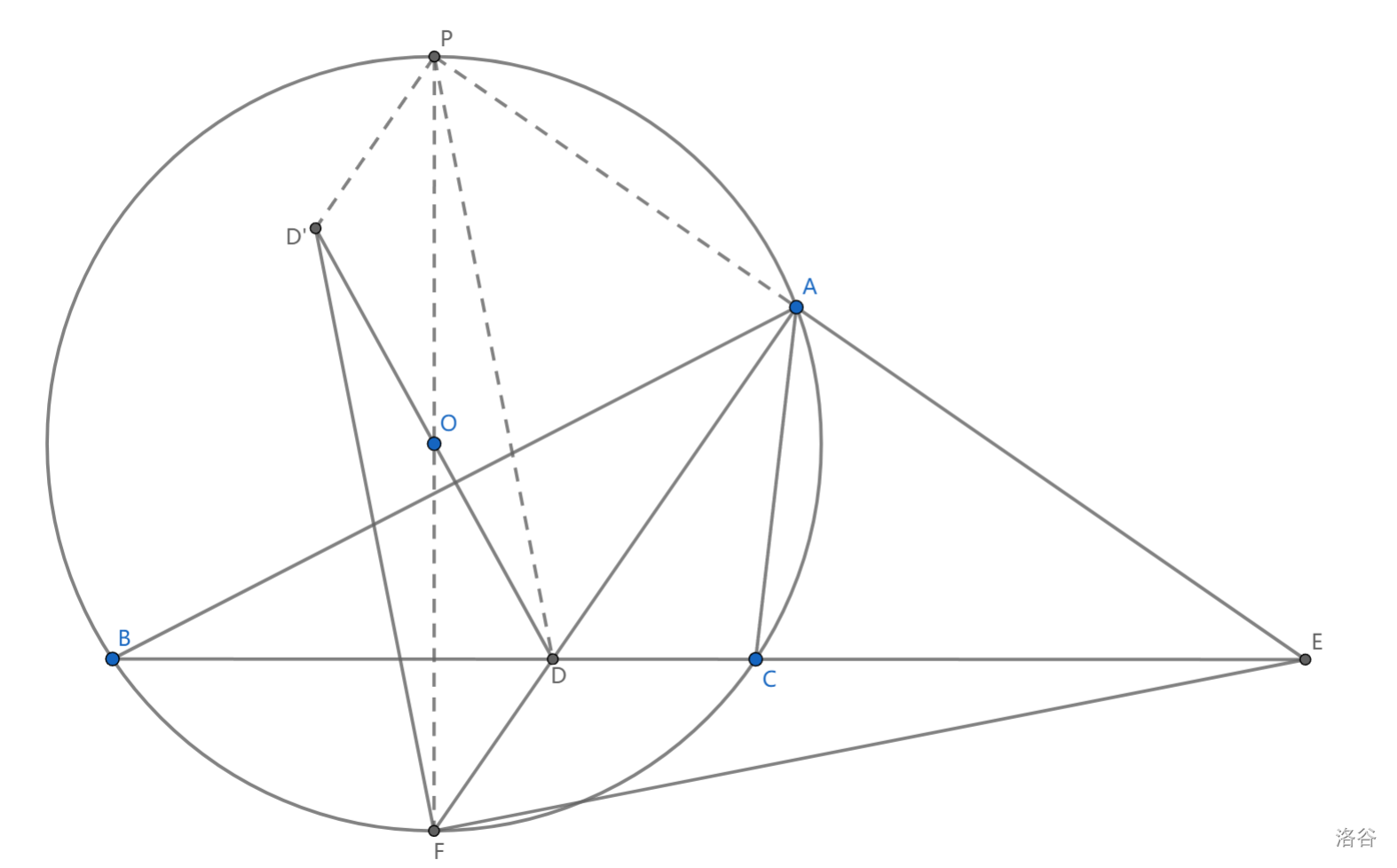
如图， \(\triangle ABC\) 内接于圆 \(O\) ，\(\angle BAC\) 内外角平分线分别交 \(BC\) 于 \(D,E\) ， \(F\) 为弧 \(BC\) 中点， \(D'\) 为 \(D\) 关于点 \(O\) 对称点，求证： \(D'F\perp FE\)

处理对称点有什么方法呢？可能很多，不过这里是关于点 \(O\) 的对称点，这可不错，我们可以再找一些圆上的点，然后得到一些对径点。

构造 \(F\) 关于 \(O\) 对称点 \(P\) ，由 \(FP\) 为直径， \(\angle PAF=Rt\angle\) ，可知 \(PAE\) 共线

本题更关键的部分是发现 \(ED\perp PF,FD\perp PE\) ，即 \(D\) 为 \(\triangle PEF\) 垂心，则 \(PD\perp EF\)

又 \(PDFD'\) 为平行四边形，所以 \(D'F\perp FE\)

总是应当敏锐地发现一些特殊的点（而不是说，题目循规蹈矩地构造出来了某个特殊点，你才能发现）

例3

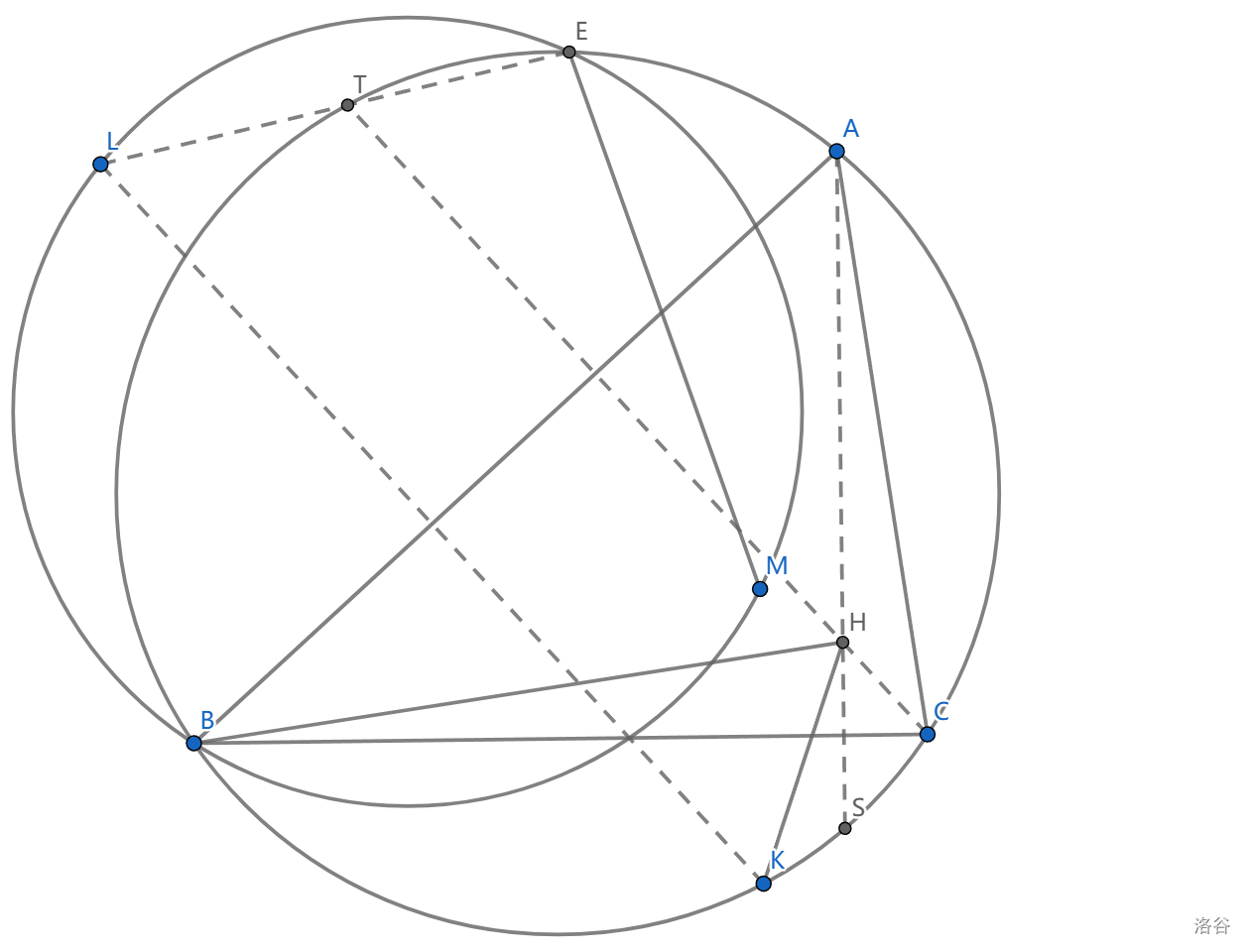
如图， \(\Gamma\) 是 \(\triangle ABC\) 外接圆， \(K\) 在弧 \(BC\) 上， \(L\) 是 \(K\) 关于 \(AB\) 的对称点， \(M\) 是 \(K\) 关于 \(BC\) 的对称点， \(E\) 是 \(\odot(BLM)\) 与 \(\Gamma\) 的交点， \(H\) 是垂心，证明： \(HK,BC,EM\) 共点。

我们首先要转换问题，我们会说：既然 \(K,M\) 关于 \(BC\) 对称，我们就取 \(H\) 关于 \(BC\) 对称点 \(S\) ，然后题目等价于证明 \(EMS\) 共线。

共线还是难以处理，既然 \(E\) 是两圆交点这种奇怪的点，我们就直接令 \(E'=SM\cap \Gamma\) ，然后证明 \(BLE'M\) 共圆即可

导角，我们会选择的是 \(\angle LBM=\angle LBK-\angle MBK=2(\angle ABK-\angle BCK)=2\angle ABC\) ，以及 \(\angle SE'L\)

\(\angle SE'L=\pi-2\angle ABC\) ，如果设 \(E'L\cap \Gamma=T\) ，我们会意识到 \(T\) 只与 \(\triangle ABC\) 有关，然后很快看到它是 \(H\) 关于 \(AB\) 的对称

实际上 \(\angle TE'L=\pi-\angle TBL=\pi-2\angle ABC\)

我们最后要证明一个共线，这里可以导角了，我们证 \(\angle LTB=\pi-\angle ETB\) ，其中 \(\angle LTB=\angle KHB=\angle MSB=\angle E'SB\) ，证毕。

九点圆

基于鸭爪定理，关于 \(H\) 对外接圆进行比例 \(2:1\) 的位似，我们会得到垂足三角形的外接圆。

这个圆上还有 \(AH,BH,CH\) 的中点和 \(\triangle ABC\) 三边中点，被称为九点圆。

同时 \(OGH\) 是共线的，满足 \(OG:GH=1:2\)

例1

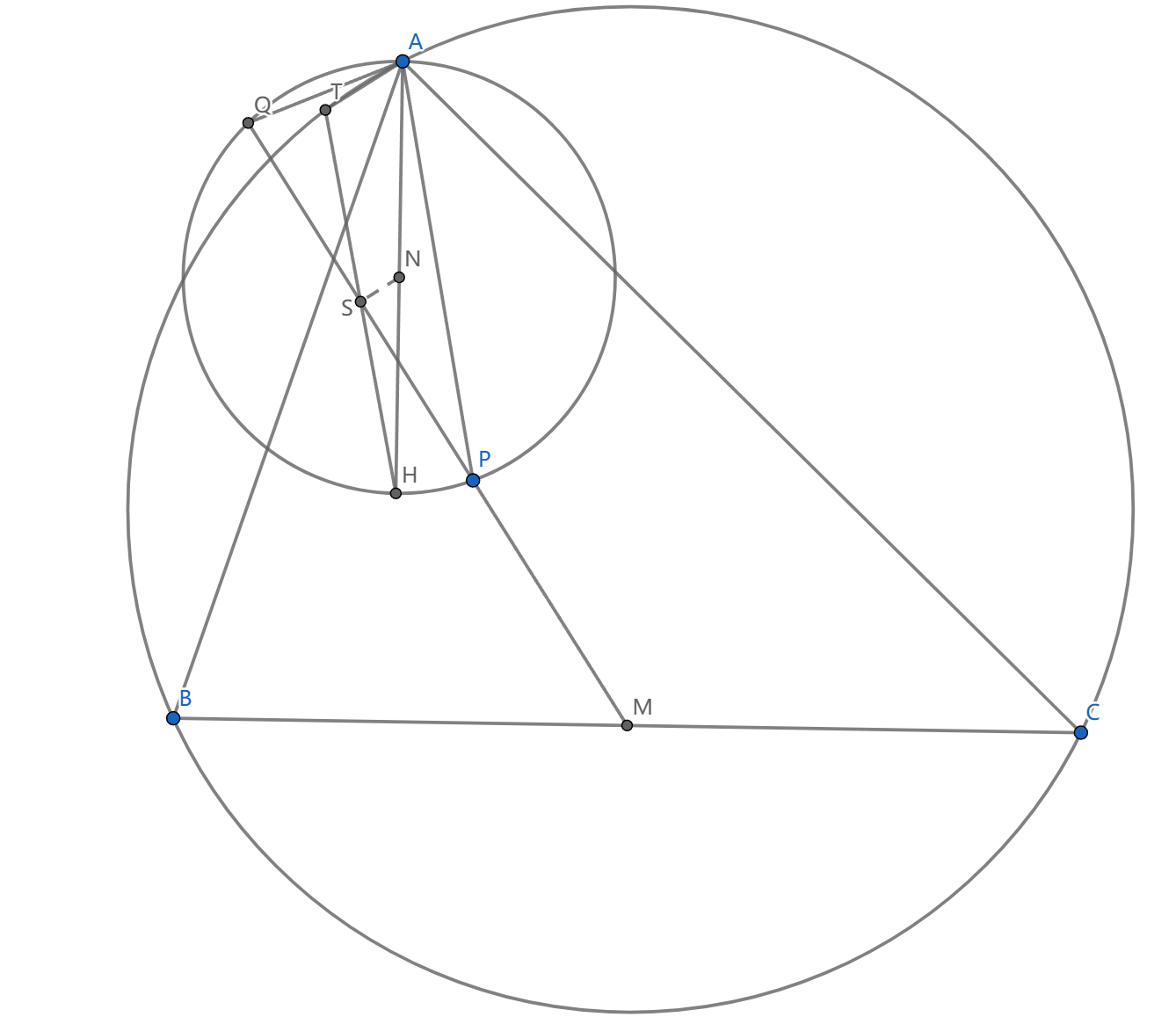
如图， \(\triangle ABC\) 的垂心是 \(H\) ， \(M\) 是中点，过 \(M\) 的动直线与 \(AH\) 为直径的圆交于 \(P,Q\) ，求证： \(\triangle APQ\) 的垂心在 \((ABC)\) 上

设出 \(APQ\) 的外心也就是 \(AH\) 中点 \(N\) 。取 \(PQ\) 的中点 \(S\) ，根据垂心与外心的性质，我们看到 \(AT=2NS\) 并且它们平行，而 \(N\) 已经是 \(AH\) 中点，所以 \(S\) 必须是 \(TH\) 中点。

现在 \(\angle MSN=Rt\angle\) 说明 \(S\) 在九点圆上（ \(MN\) 是直径这一点请务必记住！），而 \(T\) 是 \(S\) 关于 \(H\) 按 \(1:2\) 位似的结果，它在外接圆上。

例2

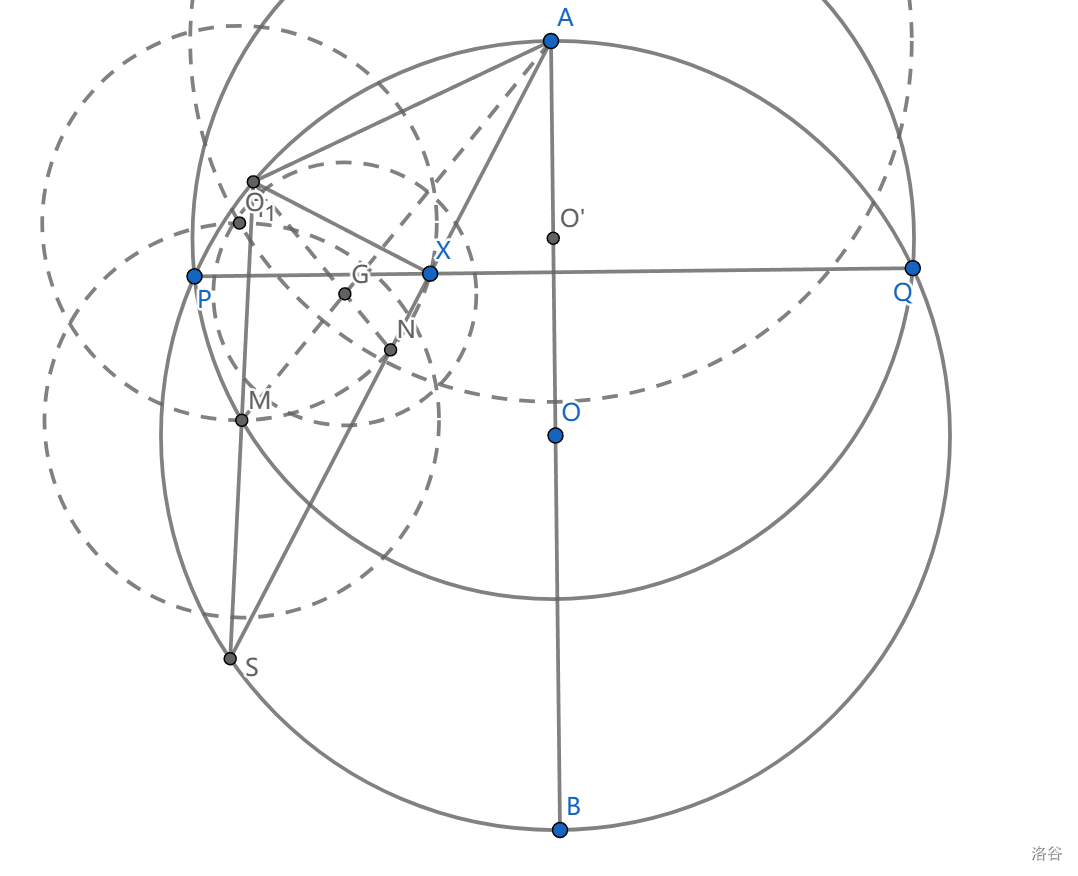
如图， \(AB\) 是 \(\odot O\) 直径， \(P,Q\) 是圆上关于 \(AB\) 对称的两点，满足 \(AP<BP\) ， \(X\) 是线段 \(PQ\) 上的动点， \(T\) 是弧 \(AQB\) 上满足 \(XT\perp AX\) 的一点。设 \(M\) 是弦 \(ST\) 的中点。当 \(X\) 在 \(PQ\) 上移动时，求证： \(M\) 在定圆上。

这题可以直接找特殊情况，然后发现圆，直接计算即可。下面是一种纯几何做法。

我们作 \(AST\) 的九点圆（这无疑是需要勇气的），设出 \(AS\) 中点 \(N\) 。由 \(A\) 是弧中点，熟知 \(AX\cdot AS=\frac 14 PQ^2\) ，从而 \(AX\cdot AN\) 是定值， \(A\) 关于九点圆的圆幂是定值，所以九点圆圆心 \(O_1\) 在定圆 \(A\) 上。

接下来关于圆心 \(O\) 对这个定圆作位似，位似比为 \(\frac 23\) ，将 \(O_1\) 变为 \(\triangle AST\) 的重心 \(G\) ， \(G\) 在定圆上

再关于 \(A\) 对这个定圆做位似比为 \(\frac 32\) 的位似，现在 \(M\) 在定圆上。

例3

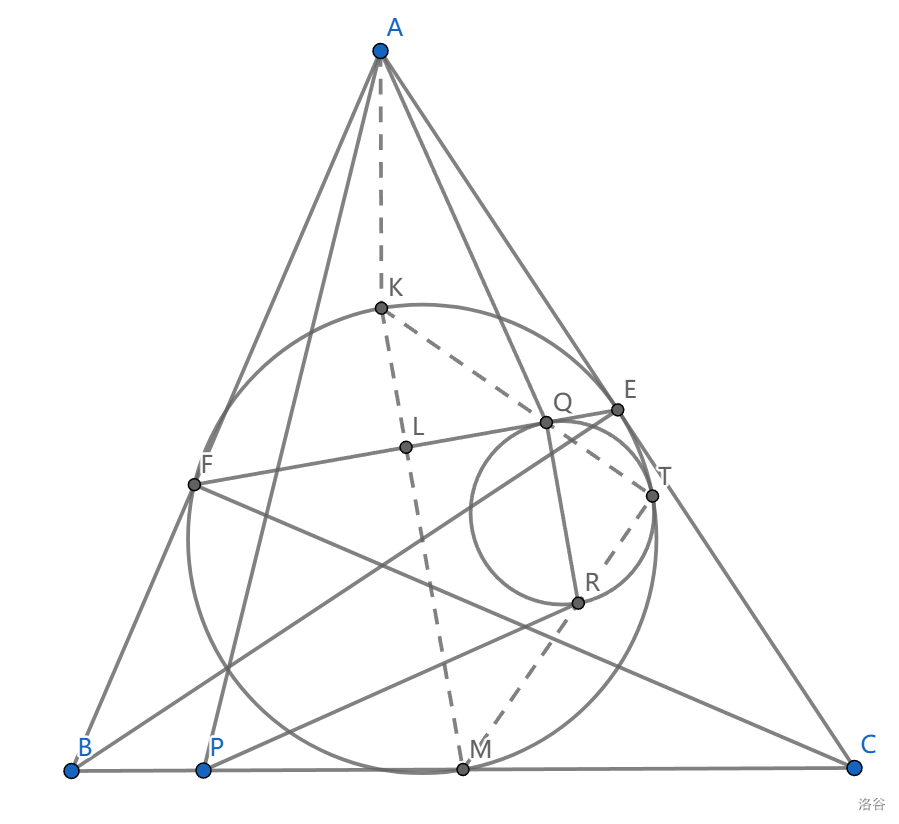
如图， \(BE,CF\) 是 \(\triangle ABC\) 的两条高，点 \(P\) 和 \(Q\) 分别在线段 \(BC,EF\) 上， \(\angle BAP=\angle CAQ\) ，点 \(R\) 满足 \(PR\perp AQ,QR\perp EF\) ，求证：以 \(QR\) 为直径的圆与 \(\triangle ABC\) 相切。

相切即关于切点位似，我们找到 \(QR\) 对应的直径 \(KM\) （与 \(EF\) 垂直），然后证明 \(KQ\cap MR\) 在两圆上，这等价于说 \(KQ\perp MR\)

直接处理这两条线看上去就毫无希望，于是我们看看条件 \(PR\perp AQ\) ，结合 \(AK\perp PM\) ，我们似乎应当将这两条线放入 \(\triangle AKQ\sim \triangle PMR\) 然后另两条边对应垂直就能给出这个垂直。

要证明这个相似，需要 \(\frac{AQ}{AK}=\frac{PR}{PM}\) ，前者看上去还好，但计算后者是灾难性的工作， \(PR\) 尚未得到任何刻画。

我们只能用同一法，我们将定义 \(T=KQ\cap \odot_{KM直径}\) ，然后设 \(R'=QR\cap MT\) （注意 \(QR\) 与 \(R\) 无关）（将它脱离 \(PR\) ，然后用点 \(T\) 生成）

在这样的条件下，我们有 \(KT\perp MT\) ，于是 \(MR'\perp KQ\) ，则对应边垂直给出 \(\triangle MR'P\sim \triangle KQA\)

我们要证 \(R'\in \odot_{QR直径}\) ，也就是 \(\angle QTR'=Rt\angle\)

我们还没利用过等角线的条件，这个条件说明 \(P,Q\) 是 \(\triangle AEF\sim\triangle ABC\) 的对应点，然后导比例（这个结论不像是能导角导出来的，实际上，我们的相似用角关系生成，应当给出比例关系）

通过线段证明垂直有不少的方法，而这里最优的很明显是我们证明 \(\triangle KLQ\sim\triangle KTM\) ，于是我们要证明 \(\frac{MR'}{KQ}=\frac{LQ}{KL}\) （注意 \(QR'//KM\) ）

我们先有 \(\frac{MR'}{KQ}=\frac{MP}{AK}\) ，然后利用相似对应有 \(\frac{MP}{LQ}=\frac{AC}{AF}=\frac{KF}{KL}=\frac{AK}{KL}\) ，马上得到想要的结果。

综合问题

最后我们展示两个美好的结果。

例1

如图， \(O,H\) 是外心与垂心，点 \(D,E,F\) 在 \(BC,AB,AC\) 上，满足 \(EC=ED,FB=FD\) ， \(O'\) 是 \(\triangle ABC\) 的外心，证明： \(O'O=O'H\)

我们首先证明 \(AFOE\) 共圆。最快的方法使用了三弦定理，可以验证 \(OA\sin A=AE\sin \angle FAO+AF\sin \angle EAO\)

接下来 \(\angle OFE=\angle OAE=\angle HCB,\angle OEF=\angle HBC\) ，所以 \(\triangle OEF\sim\triangle HBC\)

此外 \(\angle EDF=\angle A\) 说明 \(\triangle EO'F\sim\triangle BOC\) ，所以 \(O',O\) 是 \(\triangle OEF\sim\triangle HBC\) 中的相似对应点

现在 \(\angle O'OH=<EF,BC>=G\) ，并且 \(\angle OFB=\angle FAO+\angle FOA=Rt\angle -C+C-G=Rt\angle-G\)

利用 \(\frac{AO}{\sin \angle OFB}=\frac{EF}{\sin A}\) ，我们看到 \(\frac{OO'}{OH}=\frac{EF}{BC}=\frac{R\sin A}{a\sin \angle OFB}=\frac 1{2\cos G}\) ，根据 \(\angle O'OH=G\) 给出结果

例2

设 \(H\) 是 \(\triangle ABC\) 的垂心， \(O\) 是其旁心三角形的外心，证明： \(OH\) 中点 \(S\) 是其中点三角形的内心。

我们取出 \(\triangle ABC\) 的内心 \(I\) 和外心 \(O'\) ，我们知道 \(O'\) 是中点三角形的垂心

我们知道 \(\triangle ABC\) 的外接圆是其旁心三角形的九点圆（因为它们是三个垂足）， \(I\) 是旁心三角形的垂心，所以 \(O'\) 是 \(OI\) 的中点

考虑中点三角形与 \(\triangle ABC\) 的位似，假设中点三角形的内心是 \(I'\) ，我们看到 \(HI=2O'I'\) 并且方向相同（其实是共线），所以 \(I'\) 就是 \(OH\) 中点，证毕。