P2532 [AHOI2012] 树屋阶梯 题解

P2532 [AHOI2012] 树屋阶梯 题解

容易发现答案是卡特兰数，那么考虑证明这一点。

考虑从左下角到右上角填满格子。

利用动态规划的思想，回忆一下某道 $IOI$ 的题目 [数字三角形]，每个格子的方案都只能由其左边或下边转移而来。可以结合图理解一下。

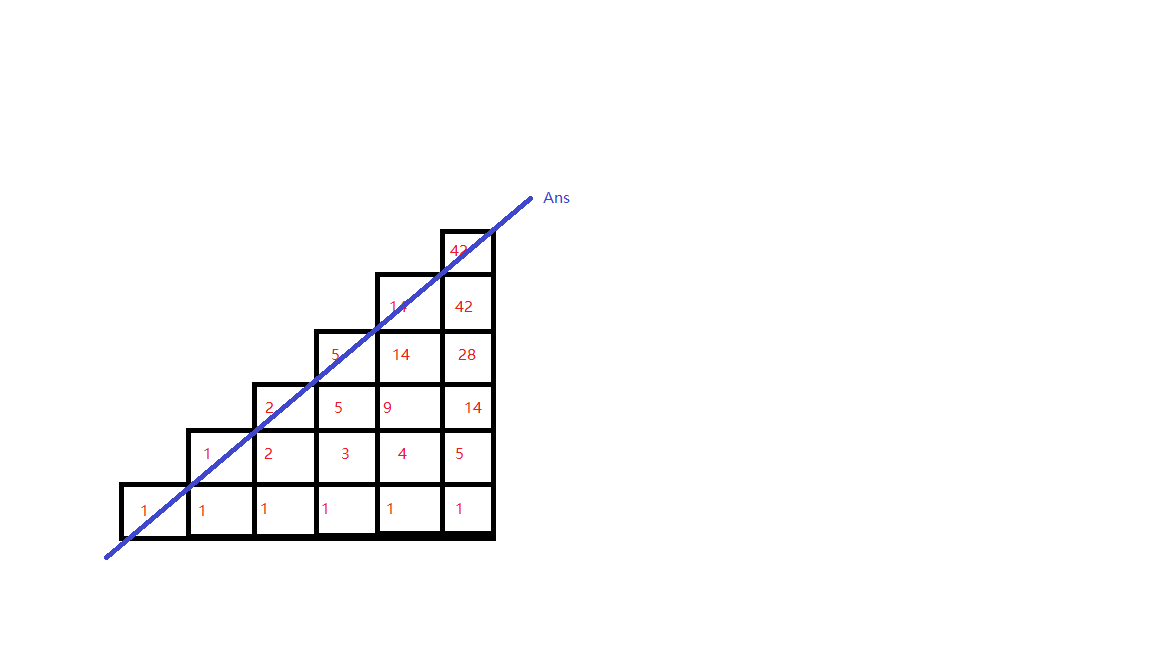
好，刚才这个定义显然很符合卡特兰数的定义，手玩的图上的数据也很支持这个观点。

代码就随便分解一下质因数，写一写高精度即可。

#include <bits/stdc++.h>
#define N 1005
using namespace std;
vector<int>v;
int prm[N];
void solve() {
	for (int i = 2; i < N; i++) {
		if (!prm[i]) {
			v.push_back(i);
			prm[i] = i;
		}
		for (auto j : v) {
			if (j * i >= N)
				break;
			prm[j * i] = j;
		}
	}
}
int cnt[N];
int a[N];
void mul(int x) {
	int tmp = 0;
	for (int i = 0; i < N - 1; i++) {
		a[i] = a[i] * x + tmp;
		tmp = 0;
		if (a[i] >= 10)
			tmp += a[i] / 10, a[i] %= 10;
	}
}
int main() {
	int n;
	cin >> n;
	solve();
	for (int i = n + 2; i <= 2 * n; i++) {
		int x = i;
		while (x > 1)
			cnt[prm[x]]++, x /= prm[x];
	}
	for (int i = 2; i <= n; i++) {
		int x = i;
		while (x > 1)
			cnt[prm[x]]--, x /= prm[x];
	}
	a[0] = 1;
	for (int i = 2; i < N; i++)
		while (cnt[i])
			cnt[i]--, mul(i);
	int len = N - 1;
	while (!a[len])
		len--;
	while (len >= 0)
		printf("%d", a[len]), len--;
	puts("");
	return 0;
}