第八章:指数模型
马科维茨的缺陷
- 每2只股票都要算协方差,\(2^n\)的数量级太大。
- 风险溢价不能预测
指数模型
分为系统性风险和公司特有风险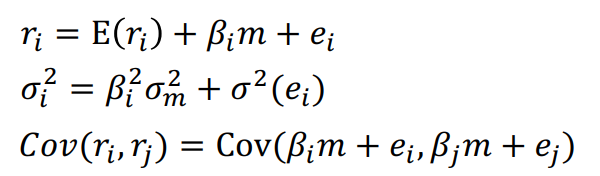
m就是市场因子
优点:
- 输入的数据少了
- 方便
单指数模型(Single-Index)回归 \(R_i=\alpha_i+\beta_iR_M+e_i\)
- R都是超额收益(-无风险利率)
- \(\beta\)是敏感系数,常用回归跑出来或者就是相关系数
![image]()
- 第一项是第二项为0时股票的期望收益,通常为0
- 第二项是市场波动带来的收益
- 残差项均值为0,协方差为0
相关参数
- 两股协方差用\(\beta\)相乘得到
- 相关系数是与市场之间的相关系数之积
![image]()
- 无论是风险溢价(期望收益)还是风险(方差)第二项永远是系统性的
对比
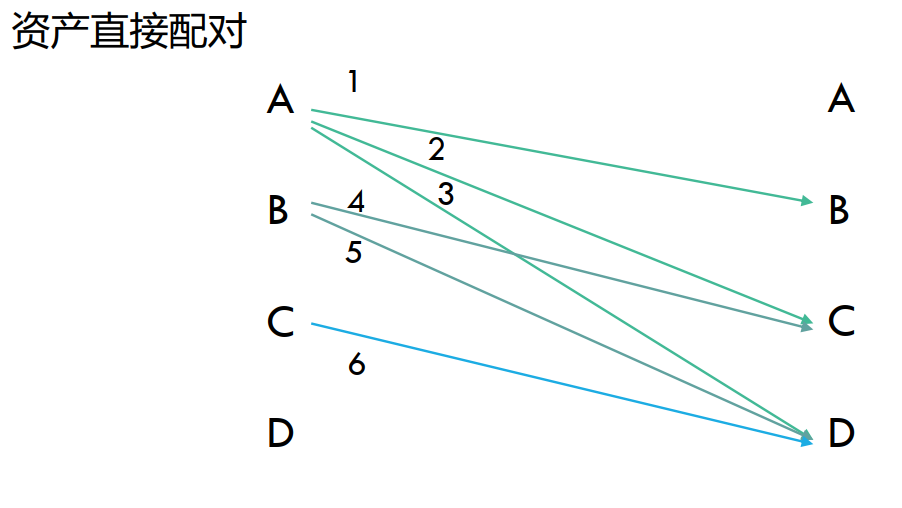
- 马科维茨
![image]()
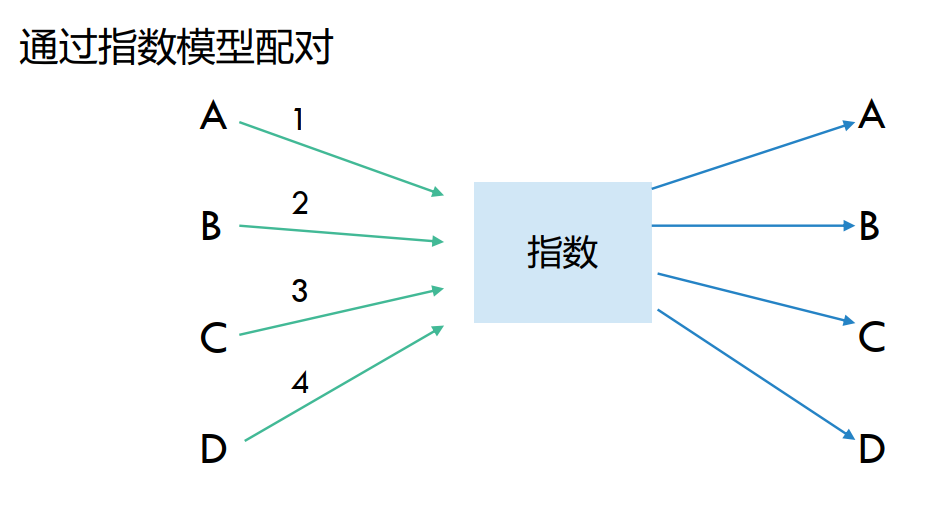
- 指数模型
![image]()
评价
- 有点太简单了,因子太少
- 减少了必要参数输入
分散化
组合方差可以计算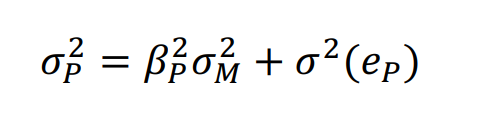
公司特有方差可以通过股票个数消除
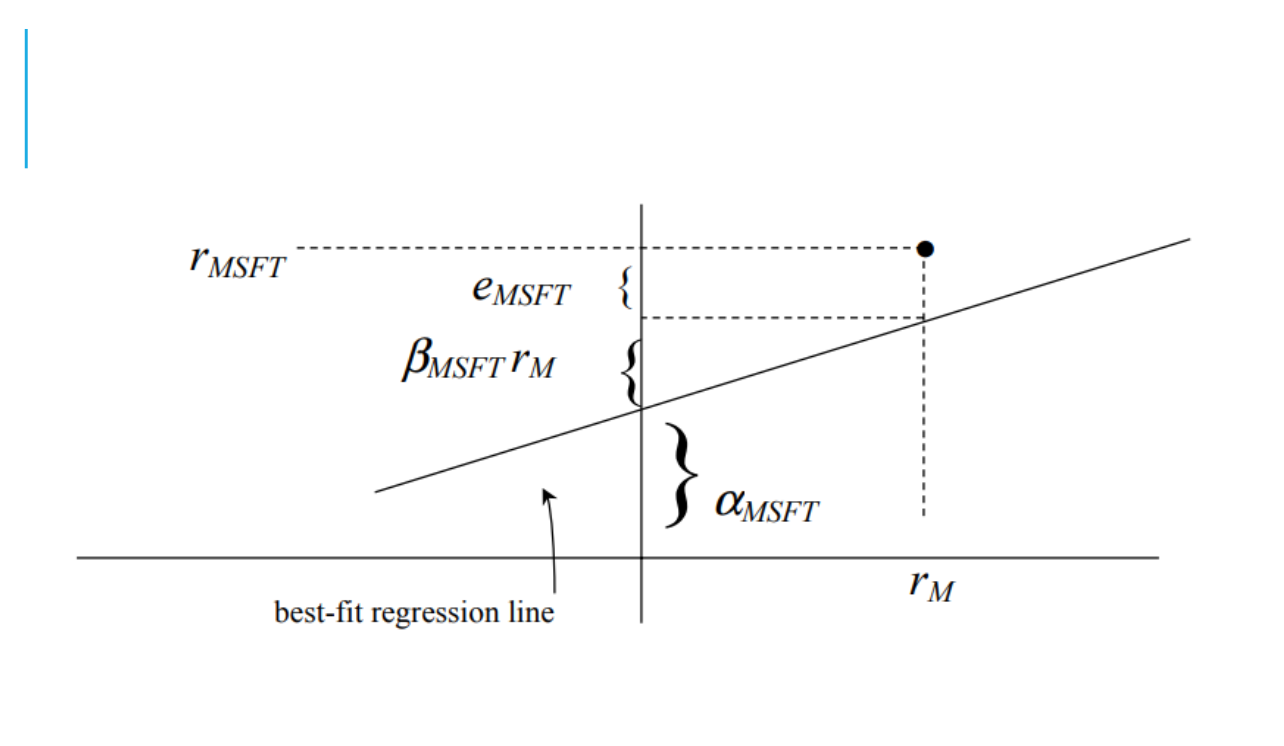
拟合的回归线叫做证券特征线![image]()
\(\alpha\)大于0是被低估,要增持(预测下来股票本身有超额收益)
最优风险组合-对标马科维茨

信息比率

最优化过程(没看懂过)

和马科维茨比
- 理论上马科维茨更精准,但是估算太多,误差积累可能实际上劣于单指数
- 单指数好处是分解了宏观和证券



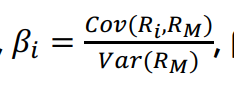
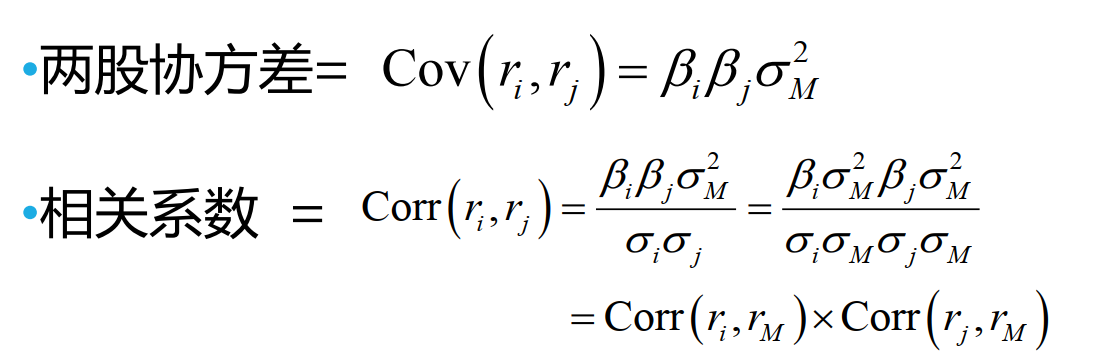

 浙公网安备 33010602011771号
浙公网安备 33010602011771号