BZOJ 1018 [SHOI2008]堵塞的交通traffic
AC通道:http://www.lydsy.com/JudgeOnline/problem.php?id=1018
分析:
为什么会只有2行呢?...于是我们就想到了:因为如果一行太水了[并查集真的可以弄么?...],如果多行好像又没那么好打了是吧...
于是想到两行也可以当做一行来玩的吧...和序列有关的,想办法来维护连通性的数据结构...
于是用到的是线段树咯:
[下图是一个2*len的区间,其中四个角分别是lu,ru,ld,rd,方便和程序里面的变量对应]

这是一个区间,我们需要维护的是四个角相互之间的联通情况,一共有六种:
luru,lurd,ldru,ldrd,luld,rurd
为什么要维护这个呢?
因为如果我们这样维护了,那么其实也就知道了所有点之间的连通情况了...
比如(x1,y1)与(x2,y2)一共有四种情况:

然后对于每一种情况,都可以用上面的那些连通性来表示。
比如我举一个第一种情况的例子,其它的情况类似:
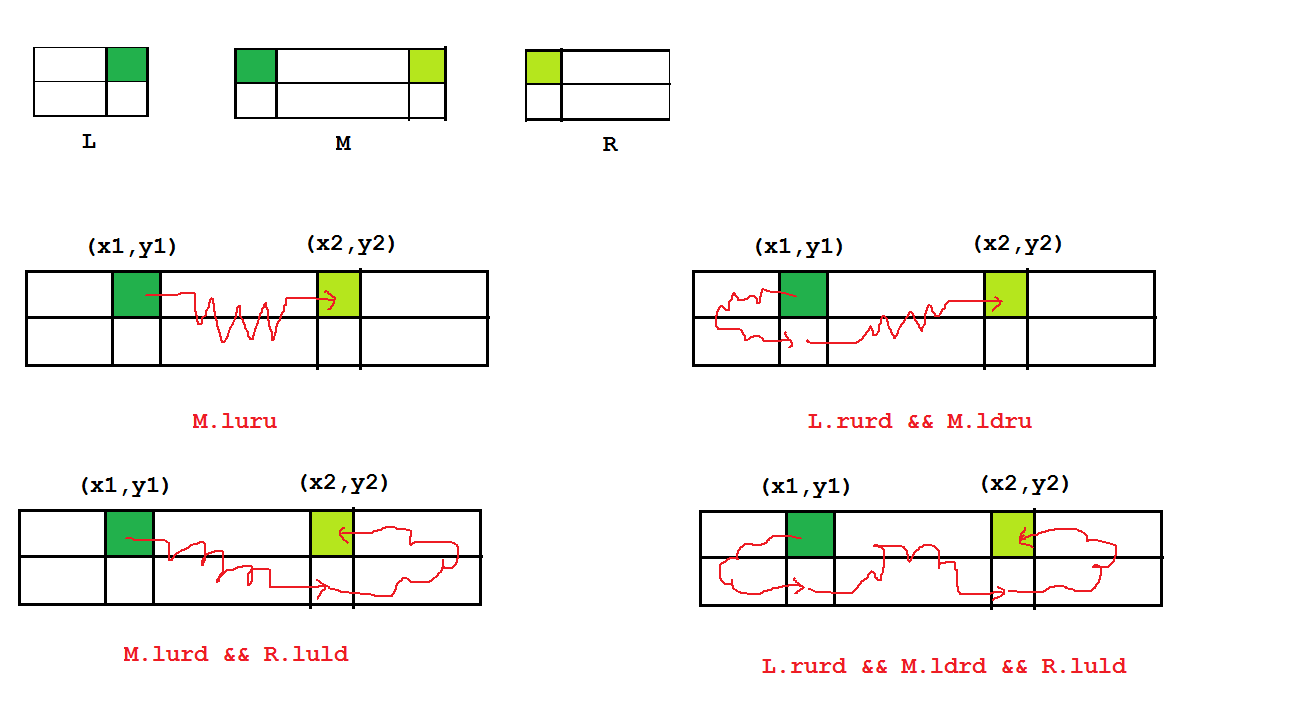
其中L表示[1,x1]的线段,M表示[x1,x2]的线段,R表示[x2,n]的线段,至于为什么需要L,R,图中也给的比较清楚了...[因为可能可以不走中间,而是从旁边绕一段来相连]
为什么画的都是曲线呢?...因为笔者想表示出这两个点之间的连接情况其实是很复杂的...只能知道它们俩是连通的而已...[所以就有一点丑了...]
然后我们知道了这样子维护一定可以求出任意两个点的连通情况,那么线段树还需要合并与修改,怎么办呢?...
那我就只举一个luru的合并过程,其它的就可以举一反三了...
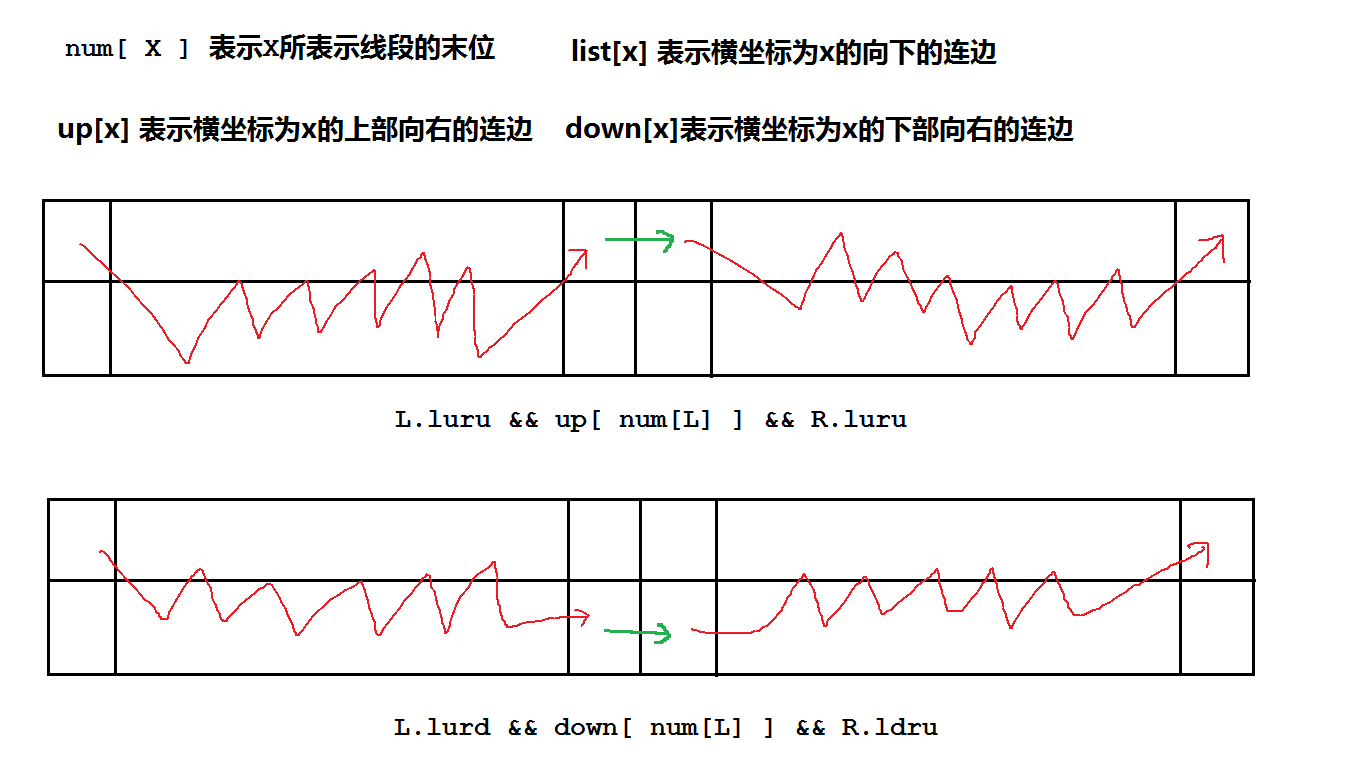
当然还有我们的边界条件?...也就是线段长度为1的时候,自然有:
luru=ldru=1;
luld=lurd=ldru=rurd=list[i];
其中list[i]表示第i个位置向下的连边。
所以修改的时候,也只需要改一下list[],up[],down[],然后更新一下一个或两个被影响的点就可以了...
代码很整齐很好看啊...很有逻辑很炫酷啊...不过有180行?...
码力提升+++

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 5 using namespace std; 6 7 inline int in(){ 8 int x=0;char ch=getchar(); 9 while(ch>'9' || ch<'0') ch=getchar(); 10 while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar(); 11 return x; 12 } 13 14 const int maxn=100010; 15 const int max_tree=maxn*5; 16 17 struct Node{ 18 bool luru,lurd,ldru,ldrd,luld,rurd; 19 // lu=left_up,ru=right_up,ld=left_down,rd=right_down; 20 }s[max_tree]; 21 22 struct Ans{ 23 bool a,b,c,d,e,f; 24 }False; 25 26 int n,x1,y1,x2,y2; 27 int num[max_tree];//标记每个节点所代表线段的右端点 28 bool up[maxn],down[maxn],list[maxn]; 29 //up[i]表示上一行中i往右是否有连边,down[i]表示下一行,list表示上下两行之间 30 31 inline void update(int o){ 32 bool a,b; 33 34 a=s[o<<1].luru && s[o<<1|1].luru && up[num[o<<1]]; 35 b=s[o<<1].lurd && s[o<<1|1].ldru && down[num[o<<1]]; 36 s[o].luru=a|b; 37 38 a=s[o<<1].luru && s[o<<1|1].lurd && up[num[o<<1]]; 39 b=s[o<<1].lurd && s[o<<1|1].ldrd && down[num[o<<1]]; 40 s[o].lurd=a|b; 41 42 a=s[o<<1].ldru && s[o<<1|1].luru && up[num[o<<1]]; 43 b=s[o<<1].ldrd && s[o<<1|1].ldru && down[num[o<<1]]; 44 s[o].ldru=a|b; 45 46 a=s[o<<1].ldru && s[o<<1|1].lurd && up[num[o<<1]]; 47 b=s[o<<1].ldrd && s[o<<1|1].ldrd && down[num[o<<1]]; 48 s[o].ldrd=a|b; 49 50 a=s[o<<1].luld; 51 b=s[o<<1].luru && s[o<<1].ldrd && s[o<<1|1].luld && up[num[o<<1]] && down[num[o<<1]]; 52 s[o].luld=a|b; 53 54 a=s[o<<1|1].rurd; 55 b=s[o<<1|1].luru && s[o<<1|1].ldrd && s[o<<1].rurd && up[num[o<<1]] && down[num[o<<1]]; 56 s[o].rurd=a|b; 57 } 58 59 void Build(int o,int l,int r){ 60 num[o]=r; 61 if(l==r){s[o].luru=s[o].ldrd=true;return ;} 62 int mid=(l+r)>>1; 63 Build(o<<1,l,mid),Build(o<<1|1,mid+1,r); 64 update(o); 65 } 66 67 void Modify(int o,int l,int r,int x){ 68 if(l==r){ 69 s[o].luru=s[o].ldrd=true; 70 s[o].luld=s[o].lurd=s[o].ldru=s[o].rurd=list[l]; 71 return ; 72 } 73 int mid=(l+r)>>1; 74 if(x<=mid) Modify(o<<1,l,mid,x); 75 else Modify(o<<1|1,mid+1,r,x); 76 update(o); 77 } 78 79 inline void Change(bool op){ 80 if(x1==x2) 81 list[x1]=op,Modify(1,1,n,x1); 82 else{ 83 if(!y1){ 84 up[x1]=op; 85 Modify(1,1,n,x1); 86 Modify(1,1,n,x2); 87 } 88 else{ 89 down[x1]=op; 90 Modify(1,1,n,x1); 91 Modify(1,1,n,x2); 92 } 93 } 94 } 95 96 Ans Query(int o,int l,int r,int al,int ar){ 97 98 if(al<=l && ar>=r) 99 return (Ans){s[o].luru,s[o].ldrd,s[o].lurd,s[o].ldru,s[o].luld,s[o].rurd}; 100 101 int mid=(l+r)>>1; 102 bool pdl=0,pdr=0; 103 Ans L,R; 104 105 if(al<=mid) 106 pdl=true,L=Query(o<<1,l,mid,al,ar); 107 if(ar>mid) 108 pdr=true,R=Query(o<<1|1,mid+1,r,al,ar); 109 110 if(pdl && pdr){ 111 bool a,b,c,d,e,f; 112 113 a=(L.a && R.a && up[num[o<<1]]) || (L.c && R.d && down[num[o<<1]]); 114 b=(L.d && R.c && up[num[o<<1]]) || (L.b && R.b && down[num[o<<1]]); 115 c=(L.a && R.c && up[num[o<<1]]) || (L.c && R.b && down[num[o<<1]]); 116 d=(L.d && R.a && up[num[o<<1]]) || (L.b && R.d && down[num[o<<1]]); 117 e=(L.e) || (L.a && L.b && R.e && up[num[o<<1]] && down[num[o<<1]]); 118 f=(R.f) || (R.a && R.b && L.f && up[num[o<<1]] && down[num[o<<1]]); 119 120 return (Ans){a,b,c,d,e,f}; 121 } 122 else if(pdl) return L; 123 else if(pdr) return R; 124 else return False; 125 } 126 127 inline bool ask(){ 128 Ans l,r,m; 129 130 m=Query(1,1,n,x1,x2); 131 l=Query(1,1,n,1,x1); 132 r=Query(1,1,n,x2,n); 133 134 if(!y1 && !y2) 135 return m.a || (l.f && m.d) || (m.c && r.e) || (l.f && m.b && r.e); 136 if( y1 && y2) 137 return m.b || (l.f && m.c) || (m.d && r.e) || (l.f && m.a && r.e); 138 if(!y1 && y2) 139 return m.c || (l.f && m.b) || (m.a && r.e) || (l.f && m.d && r.e); 140 if( y1 && !y2) 141 return m.d || (l.f && m.a) || (m.b && r.e) || (l.f && m.c && r.e); 142 } 143 144 int main(){ 145 #ifndef ONLINE_JUDGE 146 freopen("1018.in","r",stdin); 147 freopen("1018.out","w",stdout); 148 #endif 149 150 char ord[6]; 151 152 scanf("%d",&n); 153 Build(1,1,n); 154 while(~scanf("%s",ord)){ 155 if(ord[0]=='E') return 0; 156 157 y1=in(),x1=in(),y2=in(),x2=in();y1--,y2--; 158 159 if(x1>x2){swap(x1,x2);swap(y1,y2);} 160 161 if(ord[0]=='O') Change(1); 162 else if(ord[0]=='C') Change(0); 163 else{ 164 if(ask()) puts("Y"); 165 else puts("N"); 166 } 167 } 168 169 return 0; 170 }





 浙公网安备 33010602011771号
浙公网安备 33010602011771号