傅里叶变化的理解

本帖集大家之大成，感谢这位大哥：https://www.cnblogs.com/wjy-lulu/p/8319468.html
傅里叶变换是把时域信号转变为频域信号，本质上是两个不同的数学模型之间的转换。对应的是傅里叶级数。周期性信号可以转变为傅里叶级数，非周期信号可以看作是多个不同频率周期性三角波的组合（看似是复杂化信号，但是实际上这样是让信号在频域上简单）。如图所示


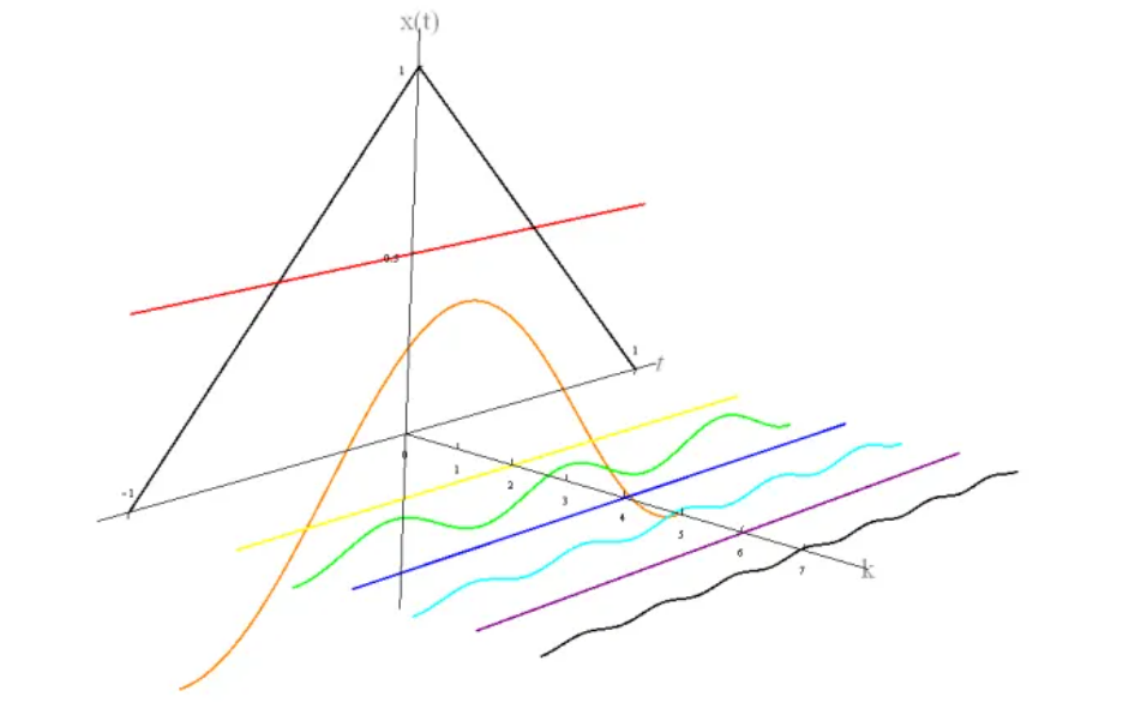
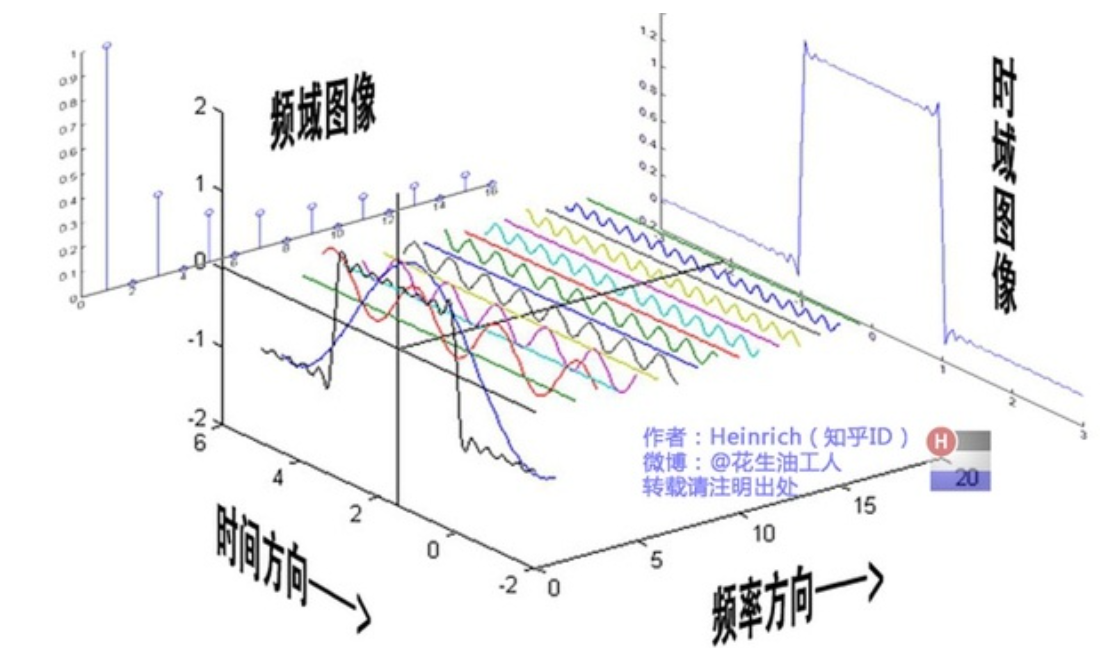
为什么我们要用正弦曲线来代替原来的曲线呢？如我们也还可以用方波或三角波来代替呀，分解信号的方法是无穷多的，但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单，因为正余弦拥有原信号所不具有的性质：正弦曲线保真度。一个正余弦曲线信号输入后，输出的仍是正余弦曲线，只有幅度和相位可能发生变化，但是频率和波的形状仍是一样的。且只有正余弦曲线才拥有这样的性质，正因如此我们才不用方波或三角波来表示。
信号正交基分解（cos和sin乘积积分为0，从而来分解复杂函数）
https://mp.weixin.qq.com/s?__biz=MzkyOTM5NjM3Mg&mid=2247483778&idx=1&sn=2ec3fa619c3396ba5550320e6663bade&scene=21#wechat_redirect
证明

有了正交基，从而将复杂函数一步步分解





欧拉公式




（注意傅里叶级数和傅里叶函数变换的区别，前者是离散的，后者可看成连续）


举例说明，以门波为例

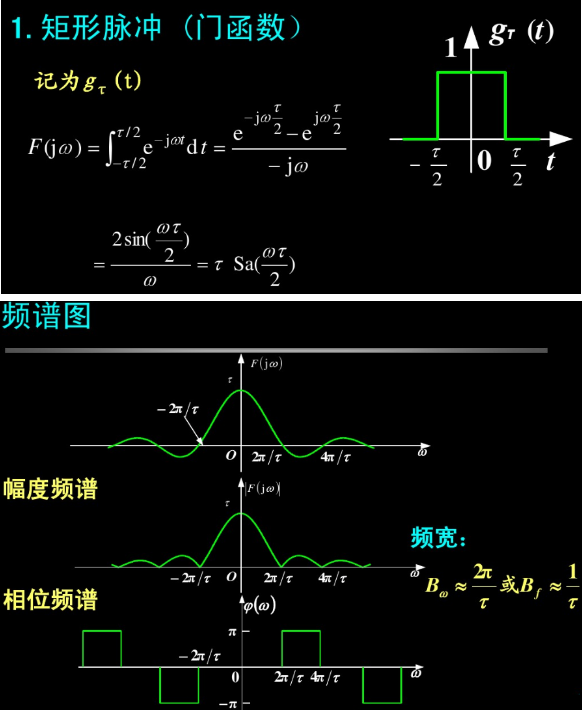
（频谱图=幅频图+相频图，所以Sa函数的相频为0或+-Π）
为什么有有负频率
https://mp.weixin.qq.com/s?__biz=MzkyOTM5NjM3Mg&mid=2247483796&idx=1&sn=60b1ffd95da04e49b3a5b05219020353&scene=21#wechat_redirect