机器学习 | 剖析感知器算法 & Python实现

前言：本系列博客参考于 《机器学习算法导论》和《Python机器学习》

如有侵权，敬请谅解。本书尽量用总结性的语言重述本书内容，避免侵权。

上一篇已经初步介绍了机器学习相关知识，简短介绍了机器学习的分类等等，本篇介绍其中监督学习中的分类领域下的感知器算法。

---

\[QAQ \]

---

本篇将循序渐进的实现一个感知器，并且通过训练使其具备对鸢尾花数据集中数据进行分类的能力。

早期的机器学习

在详细讨论感知器和相关算法之前，先大体了解一下早期机器学习的起源。 为了理解大脑的工作原理以涉及人工智能系统，沃伦*麦卡洛克 和 沃尔特*皮茨 在 \(1943\)​ 年 神经元是大脑中相互连接的神经细胞，这些细胞可以处理和传递化学和电信号。

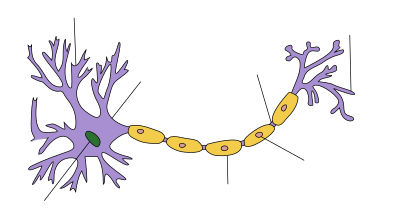
麦卡洛克-皮茨 将神经细胞描述为一个具备二进制输出的逻辑门。

树突接收多个输入信号，如果累加的信号超过某一阈（yu）值，经细胞体的整合就会生成一个输出信号，并通过轴突进行传递。

正是基于以上 \(MCP\) 模型，感知器学习法则被提出来。

感知器

Description

$MCP$ 模型出现几年后，弗兰克*罗森布拉特提出了第一个感知器学习法则。 在此感知器规则中，罗森布拉特提出了一个自学习算法，此算法可以自动 在监督学习与分类中，类似算法可用于预测样本所属的类别。
更严谨的讲，我们可以把这个问题看作一个二值分类，为了简单起见，把两类分别记为 $1$（正类别）和 $-1$（父类别）。 定义一个激活函数(activation function), 它以特定的输入值x与相应的权值向量w的线性组合作为输入。

转化成公式长这个样子：

\[\begin{array}{c} \phi(z)=w_{1} * x_{1}+w_{2} * x_{2}+\ldots+w_{m} * x_{m}=\sum_{m=0}^{m} w_{j} x_{j}=w^{T} x \\ w=\left\{\begin{array}{c} w_{1} \\ w_{2} \\ \cdots \\ w_{m} \end{array}\right\}, x=\left\{\begin{array}{c} x_{1} \\ x_{2} \\ \cdots \\ x_{m} \end{array}\right\} \end{array} \]

此时，对于一个特定样本 \(x_i\) 的激活，如果其值大于预设的阈值 \(a\)，我们将其划为 \(1\) 类，否则为 \(-1\) 类。在感知器算法中，激活函数（如下公式）

\[\phi(z)=w_{1} * x_{1}+w_{2} * x_{2}+\ldots+w_{m} * x_{m}=\sum_{m=0}^{m} w_{j} x_{j}=w^{T} x \]

\(\phi(z)\) 是一个简单的分段函数

\[\phi(z)=\left\{\begin{array}{ll} 1, & \text { 若 } \mathrm{z}>=\mathrm{a} \\ -1, & \text { 其他 } \end{array}\right. \]

\(MCP\) 神经元和罗森布拉特阈值感知器的理念就是，

通过模拟的方式还原大脑中单个神经元的工作方式：他是否被激活。

总结的来说，罗森布拉特感知器最初的规则非常简单，可总结如下几步：

1. 将权重初始化为 \(0\)​ 或者是一个极小的随机数
2. 迭代所有训练样本，执行以下操作：
   1. 根据以上公式，计算输出值
   2. 更新权重

这里的输出值是指通过前面定义的单位阶跃函数预测得出的类标，而每次对权重向量中每一权重 \(w\) 的更新方式为：

\[w_{j}:=w_{j}+\Delta w_{j} \]

对于用于更新权重的值可以通过感知器学习规则计算获得：

\[\Delta w_{j}=\eta\left(y^{(i)}-\hat{y}^{(i)}\right) x_{j}^{(i)} \]

其中 \(η\) 是学习速率（一个介于 \(0.0\) 到 \(1.0\) 之间的常数）

\(y^{(i)}\) 是第 \(i\) 个样本的真实类标（即真实值）

\(\hat{y}^{(i)}\) 是第 \(i\) 个样本的预测类标（预测值）。需要注意的是，权重向量中的所有权重值是同时更新的，这意味着在所有的权重 \(\Delta w_{j}\) 更新前，我们无法重新计算 \(\hat{y}^{(i)}\)

具体的，对于一个二维数据集，可通过下世进行更新：

\[\begin{array}{c} \Delta w_{0}=\eta\left(y^{(i)}-\text { output }^{(i)}\right) \\ \Delta w_{1}=\eta\left(y^{(i)}-\text { output }^{(i)}\right) x_{1}^{(i)} \\ \Delta w_{2}=\eta\left(y^{(i)}-\text { output }^{(i)}\right) x_{2}^{(i)}\\ ... \end{array} \]

---

\[QAQ \]

---

接下来介绍感知器的内核（推导过程），体验一下感知器规则的简洁之美（TQL

1. 对于如下式所示的两种场景，若感知器对类标的预测正确，权重可不做更新：

   \[\begin{array}{l} \Delta w_{j}=\eta\left(-1^{(i)}-(-1)^{(i)}\right) x_{j}^{(i)}=0 \\ \Delta w_{j}=\eta\left(1^{(i)}-1^{(i)}\right) x_{j}^{(i)}=0 \end{array} \]

2. 在类标预测错误的情况下，权重的值会分别趋向于正类别或者负类别的方向：

   \[\begin{array}{l} \Delta w_{j}=\eta\left(-1^{(i)}-1^{(i)}\right) x_{j}^{(i)}=-2 \eta x_{j}^{(i)} \\ \Delta w_{j}=\eta\left(1^{(i)}-(-1)^{(i)}\right) x_{j}^{(i)}=2 \eta x_{j}^{(i)} \end{array} \]

解释：假定 \(x_{j}^{(i)}=0.5\) 且模型将此样本错误的分类到了 \(-1\) 类别内。在此情况下，我们应将相应的权值增 \(1\) ，以保证下次遇到此样本时使得激活函数：\(x_{j}^{(i)}=w_{j}^{(i)}\)

能将其更多的判定为正类别，这也相当于增大其值大于单位阶跃函数阈值的概率，以使得样本被判定为 \(+1\) 类：\(\Delta w_{j}^{(i)}=\left(1^{(i)}-(-1)^{(i)}\right) * 0.5^{(i)}=2 * 0.5=1\)

权重的更新与 \(x_{j}^{(i)}=0.5\) 成比例。例如另外一个样本 \(x_{j}^{(i)}=2\)

被错误的分类到 \(-1\) 类别中，我们应更大幅度的移动决策边界，以保证下次遇到此样本时能正确分类。

\[\Delta w_{j}^{(i)}=\left(1^{(i)}-(-1)^{(i)}\right) * 2^{(i)}=2 * 2=4 \]

注意：感知器收敛的前提是两个类别必须是线性可分的，且学习速率足够小。

如果两个类别无法通过一个线性决策边界进行划分，可以为模型在训练数据集上的学习迭代次数设置一个最大值，或者设置一个允许错误分类样本数量的阈值，否则，感知器训练算法将永远不停的更新权值

下图是感知器流程图，很权威的一张图。

上图说明了感知器如何接收样本 \(x\) 的输入，并将其与权值 \(w\) 进行加权以计算净输入（net_input）,进而净输入被传递到激活函数（在此为单位阶跃函数），然后生成值为 \(+1\) 或者 \(-1\) 的二值输出，并以其作为样本的预测类标。在学习阶段，此输出用来计算预测的误差并更新权重。

---

Python实现

上述已经深入讲解感知器的规则，下面我们用代码实现它。

我们封装一个感知器类，对外提供训练和预测接口。

具体细节可见注释。

import numpy as np

class Perceptron(object):
    """
    Perceptron:感知器
        感知器收敛的前提是：两个类别必须是线性可分的，且学习速率必须足够小，否则感知器算法会永远不停的更新权值
    """

    def __init__(self, eta=0.01, n_iter=10):
        """
        初始化感知器对象
        :param eta: float 学习速率
        :param n_iter: int 在训练集进行迭代的次数
        """
        self.eta = eta
        self.n_iter = n_iter

    def net_input(self, xi):
        """
        计算净输入
        :param xi: list[np.array] 一维数组数据集
        :return: 计算向量的点积
            向量点积的概念：
                {1，2，3} * {4，5，6} = 1*4+2*5+3*6 = 32

        description:
            sum(i*j for i, j in zip(x, self.w_[1:])) python计算点积
        """
        print(xi, end=" ")
        print(self.w_[:], end=" ")
        x_dot = np.dot(xi, self.w_[1:]) + self.w_[0]
        print("的点积是：%d" % x_dot, end="  ")
        return x_dot

    """ 计算类标 """
    def predict(self, xi):
        """
        预测方法
        :param xi: list[np.array] 一维数组数据集
        :return:
        """
        target_pred = np.where(self.net_input(xi) >= 0.0, 1, -1)
        print("预测值：%d" % target_pred, end="; ")
        return target_pred

    def fit(self, x, y):
        """
        学习、训练方法
        :param x: list[np.array] 一维数组数据集
        :param y: 被训练的数据集的实际结果
        :return:
          权值，初始化为一个零向量R的(m+1)次方，m代表数据集中纬度（特征）的数量
          x.shape[1] = (100,2) 一百行2列：表示数据集中的列数即特征数

          np.zeros(count) 将指定数量count初始化成元素均为0的数组 self.w_ = [ 0.  0.  0.]
        """

        """
        按照python开发惯例，对于那些并非在初始化对象时创建但是又被对象中其他方法调用的属性，可以在后面添加一个下划线.
        将权值初始化为一个零向量，x.shape[1] 是特征的维度数量，如鸢尾花数据 (150, 5)  self.w_ = [0,0,0,0,0,0]
        w_[0]是初始权重值0  w_[1:] 每次更新的权重值 
        """
        self.w_ = np.zeros(1 + x.shape[1])
        print(self.w_)
        # 收集每轮迭代过程中错误分类样本的数量，以便后续对感知器在训练中表现的好坏做出判定
        self.errors_ = []

        for _ in range(self.n_iter):
            errors = 0
            """
            迭代所有样本，并根据感知器规则来更新权重
           """
            for x_element, target in zip(x, y):
                """ 如果预测值（self.predict(x_element)）和实际值(target)一致，则update为0 """
                update = self.eta * (target - self.predict(x_element))
                print("真实值：%d" % target)
                self.w_[1:] += update * x_element
                self.w_[0] += update
                errors += int(update != 0.0)
            self.errors_.append(errors)
        return self

另外附上 《机器学习算法导论》书中的简易代码版本

import numpy as np

class Perceptron:
    def fit(self, X, y):
        # 学习、训练方法
        m, n = X.shape
        w = np.zeros((n, 1))
        b = 0
        done = False
        while not done:
            done = True
            for i in range(m):
                x = X[i].reshape(1, -1)
                if y[i] * (x.dot(w) + b) <= 0:
                    w = w + y[i] * x.T
                    b = b + y[i]
                    done = False
        self.w = w
        self.b = b

    def predict(self, X):
        # 预测方法
        return np.sign(X.dot(self.w) + self.b)