[读书笔记]《蛋白质结合位点预测及辅助分子对接》第1章 绪论

1.3 配体-受体相互作用原理

1.3.1 受体-配体结合的关键点

受体与配体相互作用可以表示为：

\[[\mathrm{R}]+[\mathrm{L}] \rightleftharpoons[\mathrm{RL}] \]

\[\Delta G_{\text {bind }}=-R T \ln K=\Delta H-T \Delta S, \quad K=\frac{[\mathrm{RL}]}{[\mathrm{R}][\mathrm{L}]} \]

数据表明，在蛋白质-配体结合过程中有以下特征：

1. 蛋白质和配体间空间上高度的互补性
2. 蛋白质和配体表面性质上高度的互补性，比如静电互补匹配，即正负
   电荷相对应，相互作用界面包含尽可能多的氢键、盐桥；疏水相互作用互补匹配
3. 配体一般以低能构象与蛋白质相结合

1.3.2 结合过程理论模型

锁钥模型

1894年 Emil Fisher 提出锁钥模型，认为当钥匙（配体）与锁（受体）精确匹配时，“锁”才能被打开，发生生理作用变化。这个模型中，受体和配体分子都被作为刚性结构

诱导契合模型

由 Koshland 提出，受体结合位点的形状与物理化学性质分布在结晶状态下未必与配体表现出互补性；但是当受体分子与配体分子发生相互作用时，由于结合位点具有可塑性和柔性，而在配体分子的诱导下发生构象变化，从而产生几何形状和物理化学性质上的互补性结合

构象选择-诱导模型

由 Kumar 提出，认为在溶液中，受体本身就存在着多种不同构象，构象之间相互平衡，当配体分子与特定构象的受体分子结合后，就破坏了平衡，平衡向结合构象的方向移动

1.3.3 配体-受体相互作用的物理学性质

分子间相互作用主要包括：离子或电荷基团、偶极子、诱导偶极子等之间的相互作用力，氢键力，疏水基团相互作用力及非键电子推斥力等。大多数分子间作用能在10kJ/mol以下，比通常的共价键键能小一、二个数量级，作用范围约为0.3~0.5nm

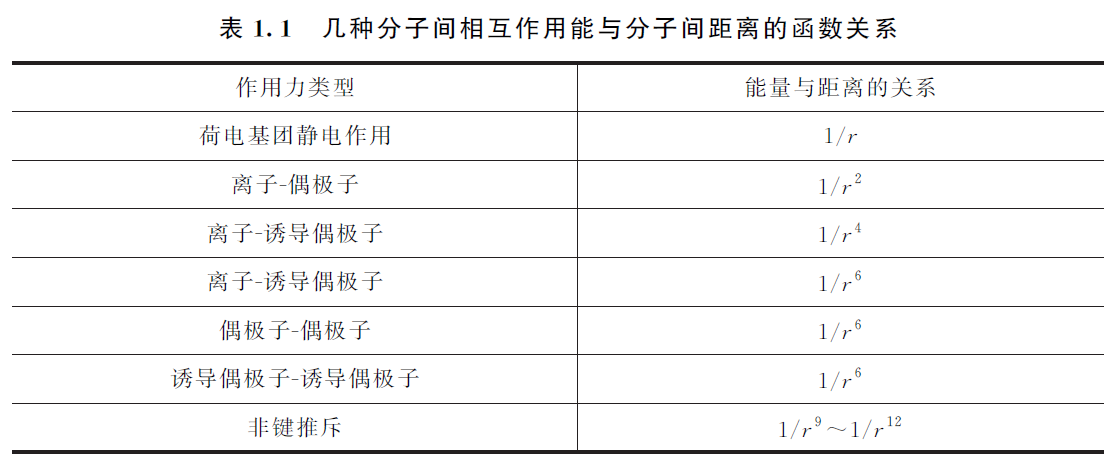
van der Waals 力

表中作用能与 \(1/r^6\) 成正比的三种力统称 van der Waals 力，范德华力的存在使得理想气体方程在实际状态下需要修正，于是引入了实际气体方程 van der Waals 方程：

\[(p+\frac{a}{V^2})(V-b)=RT \]

• （1）静电力 / 永久偶极相互作用：
  理论计算得到这种静电作用的平均能量为：

\[E_{静}=-\frac{2\mu_1^2\mu_2^2}{3kTr^6(4\pi\varepsilon_0)^2} \]

其中 \(\mu_1\)，\(\mu_2\) 是两个相互作用的分子的偶极矩，\(r\) 是分子质心之间的距离，\(k\) 是 Boltzmann 常数，T 为热力学温度，\(\varepsilon_0\) 是绝对介电常数
由此可见，静电作用与分子的偶极矩大小成正相关，而与温度负相关，因为温度升高时，破坏偶极子的取向，相互作用能也会相应降低

• （2）诱导力 / 偶极子-诱导偶极子相互作用：
  理论计算得到两个分子相互作用平均的诱导作用能为：

\[E_诱=-\frac{\mu_1^2\alpha_2}{(4\pi\varepsilon_0)^2r^6} \]

其中 \(\mu_1\) 是极性分子的偶极矩，\(\alpha_2\) 是被极化分子的极化率

• （3）色散力 / 非极性分子相互作用：
  因和计算光的色散作用类似而得名，可以看作是分子的瞬间偶极相互作用的结果。理论计算这种力的作用能是：

\[E_色=-\frac{3}{2}\frac{I_1I_2}{I_1+I_2}(\frac{\alpha_1\alpha_2}{r^6})\frac{1}{(4\pi\varepsilon_0)^2} \]

\(I_1\) \(I_2\) 是两个相互作用分子的电离能，\(\alpha_1\) \(\alpha_2\)是两个相互作用分子的极化率

实验数据表明，对大多数分子而言，色散力是主要的