[物理有机] 线性自由能相关 (Linear Free Energy Relationship)

前言

在物理有机化学中，我们希望能够通过定量的手段来解释、分析、预测以往认识有机化学中的一些经验性的东西。在研究电子效应的定量描述领域，就需要通过线性自由能相关来完成

Hammett 线性自由能相关

取代基电子效应应该怎么刻画与比较更为科学呢？

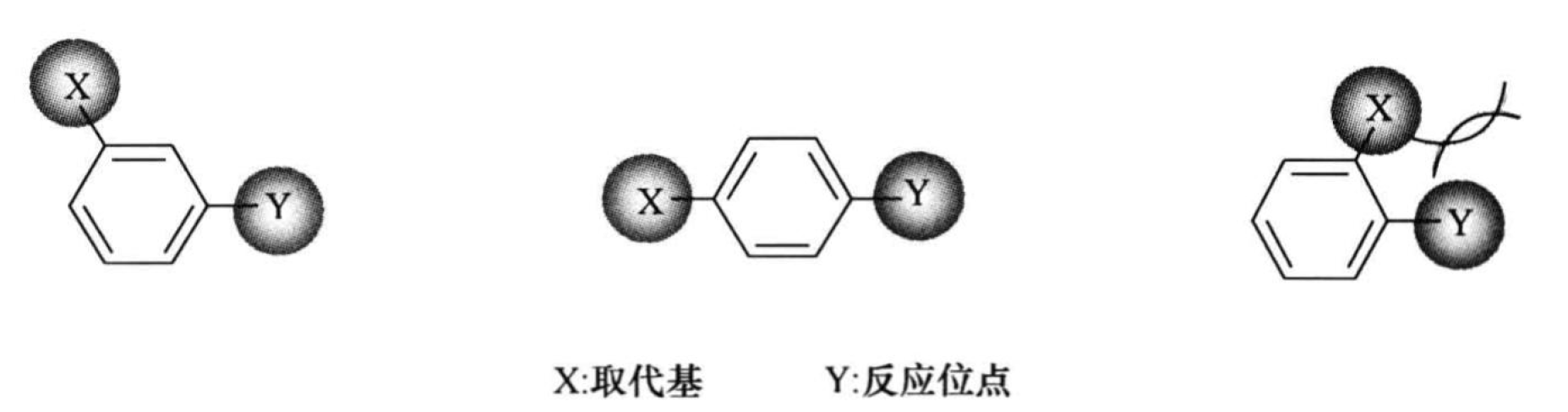
Hammett 指出，利用苯环中的\(\pi\)电子体系，电子效应可以通过苯环良好地传递到反应位点的取代基

标准：苯甲酸的取代

为了使反应位点的反应活性足够方便量化，我们规定 \(25^{\circ}C\)，\(Y = -COOH\)，作为标准，衡量取代与非取代情况下二者的电离能力：

Hammett 定义： \(\sigma = lg\frac{K}{K_o}\)
其中 \(K\) 为取代苯甲酸 \(XC_6H_4CO_2H\) 的平衡常数，\(K_o\) 为 \(C_6H_5CO_2H\) 的平衡常数，\(\sigma\) 叫做取代基常数

推广：非标准的取代

如果主体并非标准所规定的苯甲酸，而是羧酸的衍生物，那么我们就有
Hammett 方程：\(lg\frac{K}{K_o}=\rho\sigma\)
其中\(\rho\) 为反应常数，\(K\) 为取代后 \(XC_6H_4Y\) 的平衡常数，\(K_o\) 为非取代 \(C_6H_5Y\) 的平衡常数
对于苯甲酸在 \(25^{\circ}C\) 水溶液中的电离，\(\rho = 1\)

此外我们发现对于速率常数，也有：
Hammett 方程：\(lg\frac{k}{k_o}=\rho\sigma\)

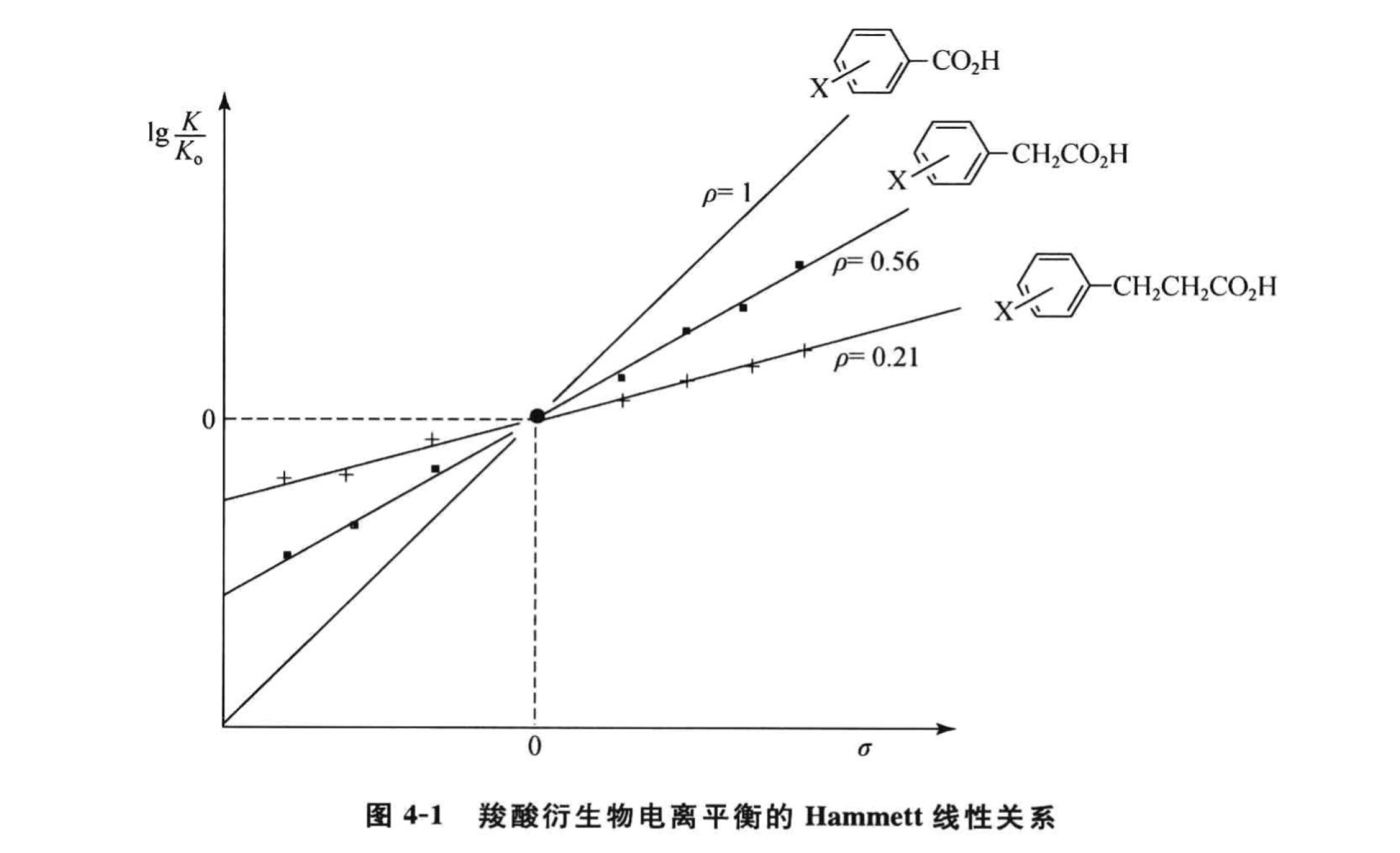
线性自由能相关

令化合物\(M = XC_6H_4CO_2H\)，因为 \(lgK = - \frac{\Delta G^\ominus}{2.303RT}\)，结合Hammett 方程，推导出方程组：
\(\begin{cases} lg\frac{K}{K_o}=\rho\sigma \\ lg\frac{k}{k_o}=\rho\sigma \\ \Delta G_X^\ominus - \Delta G_H^\ominus = \rho (\Delta G_X^\ominus - \Delta G_H^\ominus)_M \\ \Delta G_X^\ne - \Delta G_H^\ne = \rho (\Delta G_X^\ne - \Delta G_H^\ne)_M \end{cases}\)
这些方程都叫做线性自由能相关

取代基常数的意义

因为考虑的是苯环上的取代基，所以会有邻间对的位置问题。其中，如果取代基位于反应基团邻位，基团间容易发生相互作用产生干扰，所以我们一般只考虑间位和对位的取代基效应，其中 \(\sigma_p\) 表示对位，\(\sigma_m\) 表示间位

\(\sigma\) 量化了取代基的电子效应，\(\sigma > 0\)，取代基比氢的吸电子能力强，\(\sigma > 0\)，取代基比氢的给电子能力强。