Discrete Fourier Transform
此为OpenCV官方教程的个人翻译
限于目前的知识水平(刚学完高数离散线代)这篇其实没怎么看懂,先mark一下
目标
我们将寻求以下问题的答案:
- 什么是傅里叶变换,为什么要使用它?
- 如何在OpenCV中使用离散傅里叶变换?
- 函数的使用,例如:copyMakeBorder(),merge(),dft(),getOptimalDFTSize(),log()和normalize()。
源码
你可以从这里下载它,或者在OpenCV源代码库中找到它。它位于samples/cpp/tutorial_code/core/discrete_fourier_transform/discrete_fourier_transform.cpp
下面是 dft() 的示例用法:
/*
* @LastEditors: 帝皇の惊
* @Date: 2022-06-27 19:02:01
* @Description: Edit Here
* @LastEditTime: 2022-06-27 19:33:43
*/
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <iostream>
using namespace cv;
int main(int argc, char **argv)
{
const char filename[] = "E:\\Work\\Visual Studio Code\\fengmian.jpg";
Mat I = imread(filename, IMREAD_GRAYSCALE);
if (I.empty()) {
return -1;
}
Mat padded; // 扩展输入图像至合适尺寸
int m = getOptimalDFTSize(I.rows);
int n = getOptimalDFTSize(I.cols); // 用边界值和零值填充
copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0));
Mat planes[] = {Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F)};
Mat complexI;
merge(planes, 2, complexI); // Add to the expanded another plane with zeros
dft(complexI, complexI); // this way the result fit in the source martix
// compute the magnitude and switch to logarithmic scale
// => log(1 + sqrt(Re(DFT(I)))^2 + Im(DFT(I))^2)
split(complexI, planes); // planes[0] = Re(DFT(I)), planes[1]=Im(DFT(I));
magnitude(planes[0], planes[1], planes[0]); // planes[0] = magnitude
Mat magI = planes[0];
magI += Scalar::all(1); // switch to logarithmic scale
log(magI, magI);
// crop the spectrum, if it has an odd number of rows or columns
magI = magI(Rect(0, 0, magI.cols & -2, magI.rows & -2));
// rearrange the quadrants of Fourier image so that the origin is at the image center
int cx = magI.cols / 2;
int cy = magI.rows / 2;
Mat q0(magI, Rect(0, 0, cx, cy)); // Top-Left - Create a ROI per quadrant
Mat q1(magI, Rect(cx, 0, cx, cy)); // Top-Right
Mat q2(magI, Rect(0, cy, cx, cy));
Mat q3(magI, Rect(cx, cy, cx, cy));
Mat tmp;
q0.copyTo(tmp);
q3.copyTo(q0);
tmp.copyTo(q3); // 交换左上右下
q1.copyTo(tmp);
q2.copyTo(q1);
tmp.copyTo(q2); // 右上左下
normalize(magI, magI, 0, 1, NORM_MINMAX);
imshow("input image", I);
imshow("dft", magI);
waitKey(0);
return 0;
}
解释
傅里叶变换会将图像分解为其正弦和余弦分量。换句话说,它将图像从其空间域转换为其频域。事实上,任何函数都可以精确地近似于无限正弦和余弦函数之和。傅里叶变换是实现这一目标的一种方式。从数学上讲,二维图像傅里叶变换是:
此处 f 是其空间域中的图像值,F 是其频域中的图像值。转换的结果是复数。可以通过实数图像和复数图像或通过幅度(magnitude)和相位(phase)图像来显示这一点。然而,在整个图像处理算法中,只有幅度(magnitude)图像是有趣的,因为它包含我们需要的有关图像几何结构的所有信息。但是,如果您打算以这些形式对图像进行一些修改,然后需要重新进行变换,那么幅度和相位图像都将需要。
在此示例中,我将演示如何计算和显示傅里叶变换的幅度图像。这意味着它们可能从给定的域值中获取值。例如,在基本灰度中,图像值通常介于 0 和 255 之间。因此,傅里叶变换也需要是离散类型,从而产生离散傅里叶变换(DFT)。每当需要从几何角度确定图像的结构时,您都需要使用它。以下是要遵循的步骤(如果是灰度输入图像I):
-
将图像扩展到最佳大小。DFT 的性能取决于图像大小。对于数字 2、3 和 5 的倍数的图像大小,它往往是最快的。因此,为了实现最佳性能,通常最好将边框值填充到图像上,以获得具有此类特征的大小。getOptimalDFTSize() 返回此最佳大小,我们可以使用 copyMakeBorder() 函数来扩展图像的边框:
Mat padded; //expand input image to optimal size int m = getOptimalDFTSize( I.rows ); int n = getOptimalDFTSize( I.cols ); // on the border add zero pixels copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0));追加的像素初始化为零。
-
为复数值和实数值开辟空间。傅里叶变换的结果是复杂的。这意味着对于每个图像值,结果是两个图像值组合起来的(每个图像都会占一部分)。此外,频域范围比其空间域对应范围大得多。因此,我们通常至少以float格式存储这些内容。因此,我们将输入图像转换为此类型,并使用另一个通道扩展它以保存复数值:
Mat planes[] = {Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F)}; Mat complexI; merge(planes, 2, complexI); // Add to the expanded another plane with zeros -
进行离散傅里叶变换。可以进行就地计算(输入与输出相同):
dft(complexI, complexI); // this way the result may fit in the source matrix -
将实数值和复数值转换为幅度。复数有一个实数(Re)和一个复数(虚数 - Im)部分。DFT的结果是一个复数。其对应大小是:
\[M=\sqrt{Re(DFT(I))^2+Im(DFT(I))^2} \]转换为 OpenCV 代码为:
split(complexI, planes); // planes[0] = Re(DFT(I), planes[1] = Im(DFT(I)) magnitude(planes[0], planes[1], planes[0]);// planes[0] = magnitude Mat magI = planes[0]; -
进行对数转换。事实证明,傅里叶系数的动态范围太大,无法在屏幕上显示。我们有一些很小的和一些很高的值,我们无法像这样观察到。因此,高值将全部显示为白点,而小值将全部变为黑色。要使用灰度值进行可视化,我们可以将线性尺度进行对数转换:
\[M_1=\log(1+M) \]转换为 OpenCV 代码:
magI += Scalar::all(1); // switch to logarithmic scale log(magI, magI); -
裁剪和重组。还记得吗,在第一步,我们扩展了图像?好吧,是时候抛弃新引入的值了。出于可视化目的,我们还可以重新排列结果的象限,以便原点(0,0)与图像中心相对应。
magI = magI(Rect(0, 0, magI.cols & -2, magI.rows & -2)); int cx = magI.cols/2; int cy = magI.rows/2; Mat q0(magI, Rect(0, 0, cx, cy)); // Top-Left - Create a ROI per quadrant Mat q1(magI, Rect(cx, 0, cx, cy)); // Top-Right Mat q2(magI, Rect(0, cy, cx, cy)); // Bottom-Left Mat q3(magI, Rect(cx, cy, cx, cy)); // Bottom-Right Mat tmp; // swap quadrants (Top-Left with Bottom-Right) q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3); q1.copyTo(tmp); // swap quadrant (Top-Right with Bottom-Left) q2.copyTo(q1); tmp.copyTo(q2); -
规范化。出于可视化目的,再次执行此操作。我们现在有了星等,但是这仍然超出了我们0到1的图像显示范围。我们使用 normalize() 函数将值规范化到此范围。
normalize(magI, magI, 0, 1, CV_MINMAX); // Transform the matrix with float values into a // viewable image form (float between values 0 and 1).
结果
傅里叶变换的一个应用是确定图像中存在的几何方向。例如,让我们找出文本是否水平?查看一些文本,您会注意到文本行的形式也是水平线,而字母形式是垂直线。在傅里叶变换的情况下,也可以看到文本片段的这两个主要组成部分。让我们进行一个测试:
水平文本:

非水平文本:

如果是水平文本,其傅里叶变换显示的图像为:

非水平文本则显示为:
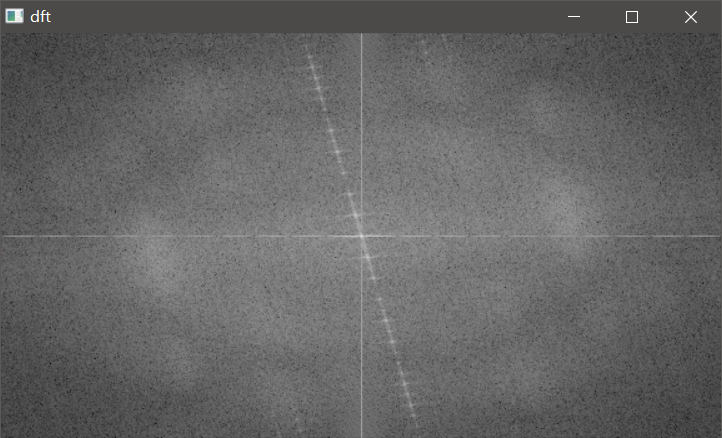
您可以看到,频域中最具影响力的分量(幅度图像上最亮的点)跟随图像上物体的几何旋转。由此,我们可以计算偏移并旋转图像使其对齐。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号