【算法】Prim算法

前言

　　最近数据结构已经结课了，但是我差的太多啦！！！这篇文章就来补最小生成树的Prim算法。

简介

　　Prim是一种生成最小生成树的算法。雀氏简啊

算法步骤描述

假设$$ N=(V, {E}) $$ 是一连通图, \(TE\)为最小生成树种边的集合。

1. 初始时\(U={u_0}(u_0\in V), TE=\empty\) 。
2. 在所有的$u\in U,v\in V-U \(的边中，选一条代价最小的边\)(u,v)\(并入集合\)TE\(,同时\)v\(并入\)U$.
3. 重复第二个步骤，直到\(U=V\)为止。

此时，\(TE\)种必含\(n-1\)条边，则\(T=(V,{TE})\)为N的最小生成树。

算法图解

此图来源于课本

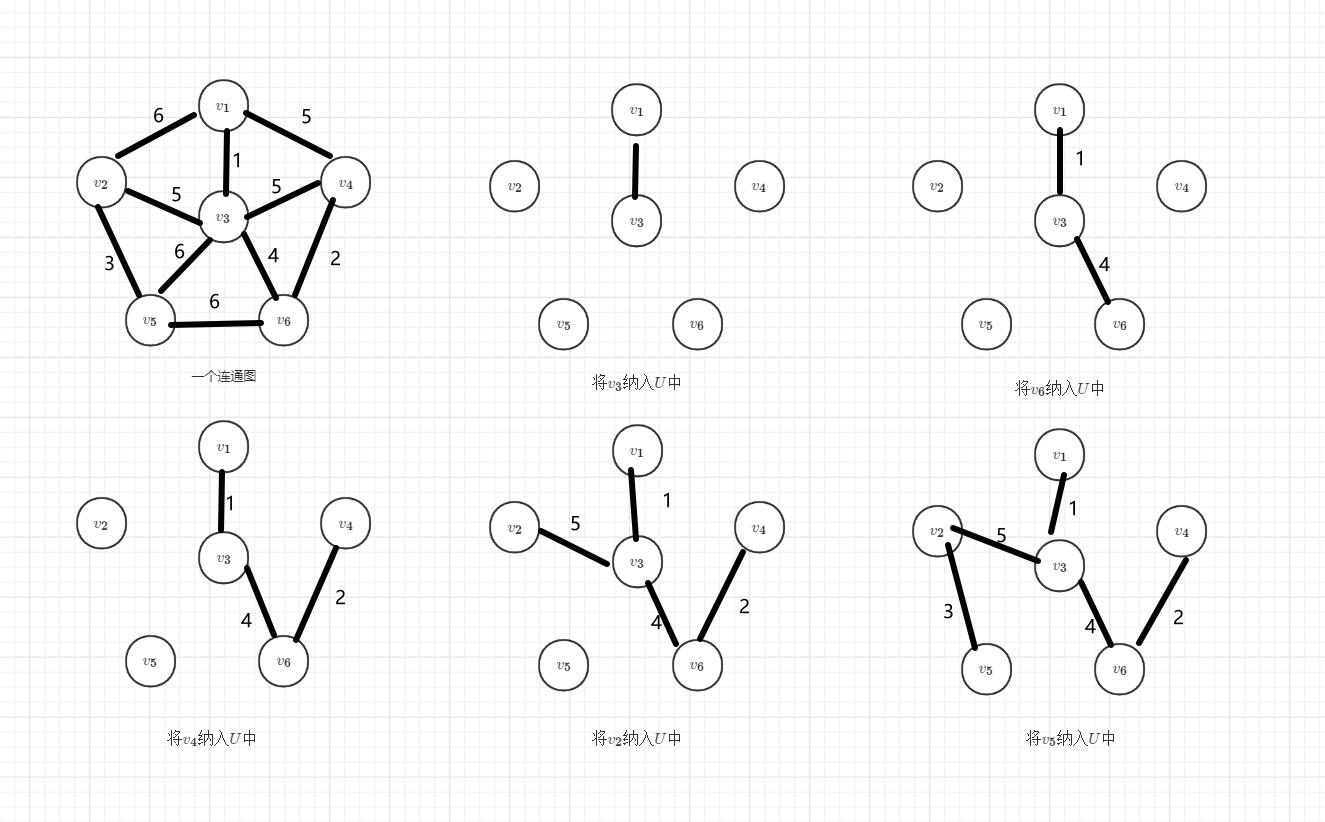
算法实现

为了记录已在生成树的顶点集\(U\)，我们使用一个结构来记录，如下

struct Assist
{
    int tail;			// 表示从结点tail引出
    int lowcost;		// 表示到当前结点的最短距离
};

在进行操作时，我们(closedge为Assist数组)

1. 将初始顶点\(u\)加入到\(U\)中，对其余每一顶点\(i\),将\(closedge[i]\)均初始化为\(i\)到\(u\)的边信息。
2. 循环\(n-1\)次，进行如下操作：
   • 在\(closedge\)中选出最小边\(closedge[v],这里v \in V-U\)。
   • 将\(v\)加入\(U\)
   • 更新剩余每组的最小边信息\(closedge[i](i \in V-U)\) 。

关键部分如下:

/**
 * @description: Prim算法
 * @param begin 最小生成树的开始结点
 * @return void
 */
void Graph::prim(int begin)
{
    /*用于求最小生成树的辅助结构*/
    Assist closedge[20];
    auto start = begin - 1;
    closedge[start].lowcost = 0; // 初始化, U = {u}
    for (int i = 0; i < vexnum; i++)
    {
        if (i != start)			// 初始化closedge[i]
        {
            closedge[i].tail = start;
            auto weig = findArc(start, i + 1);
            if (!weig)
            {
                closedge[i].lowcost = 10000;
            }
            else
            {
                closedge[i].lowcost = weig->weight;
            }
        }
    }
    for (int i = 0; i < vexnum - 1; i++)		// 循环n-1次
    {
        auto minNode = minimum(closedge);		// 找出最小边
        start = closedge[minNode].tail;
        /*输出最小生成树信息*/
        std::cout << "<" << start + 1 << "," << minNode + 1 << ">" << std::endl;
        closedge[minNode].lowcost = 0;			// 将minNode并入U中
        /*更新closedge信息*/
        for (int j = 0; j < vexnum; j++)
        {
            auto now = findArc(minNode, j + 1);
            if (!now)
            {
                continue;
            }
            if (now->weight < closedge[j].lowcost)
            {
                closedge[j].lowcost = now->weight;
                closedge[j].tail = minNode;
            }
        }
    }
}

完整代码实现

/*
 * @Author: zh(RickSchanze)(帝皇の惊)
 * @Description: 最小生成树的Prim算法
 * @Date: 2022-05-29 22:48:52
 * @LastEditTime: 2022-05-31 21:34:56
 */
#include <iostream>

struct ArcNode
{
    int arc;
    int weight;
    ArcNode *next;

    ArcNode(int arc, int weight) : arc(arc), weight(weight), next(nullptr) {}
};

struct VexNode
{
    int vex;
    ArcNode *first;

    VexNode(int vex) : vex(vex), first(nullptr) {}
    VexNode() : vex(-1), first(nullptr) {}
};

struct Assist
{
    int tail;
    int lowcost;
};

struct Graph
{
    VexNode vexMat[20];
    int arcnum;
    int vexnum;

    // void createDirectedGraph();  有向图暂时先不写了
    void createGraph();
    void prim(int begin);
    ArcNode *findArc(int begin, int end) const;
    int minimum(Assist *) const;
};

int Graph::minimum(Assist dist[]) const
{
    int min = 10000, rtn = 10000;
    for (int i = 0; i < vexnum; i++)
    {
        if (dist[i].lowcost == 0)
        {
            continue;
        }
        if (dist[i].lowcost < min)
        {
            min = dist[i].lowcost;
            rtn = i;
        }
    }
    return rtn;
}

ArcNode *Graph::findArc(int begin, int end) const
{
    auto beginPtr = vexMat[begin].first;
    if (beginPtr)
    {
        while (beginPtr != nullptr)
        {
            if (beginPtr->arc == end)
            {
                return beginPtr;
            }
            beginPtr = beginPtr->next;
        }
    }
    return beginPtr;
}

void Graph::createGraph()
{
    std::cout << "请输入顶点个数:";
    std::cin >> vexnum;
    // vexMat = new VexNode[vexnum];
    for (size_t i = 0; i < vexnum; i++)
    {
        std::cin >> vexMat[i].vex;
    }
    std::cout << "请输入边个数:";
    std::cin >> arcnum;
    for (size_t i = 0; i < arcnum; i++)
    {
        int begin, end, weight;
        std::cout << "输入弧尾弧头权重:";
        std::cin >> begin >> end >> weight;
        auto first = vexMat[begin - 1].first;
        for (; first != nullptr && first->next != nullptr; first = first->next)
            ;
        if (first == nullptr)
        {
            vexMat[begin - 1].first = new ArcNode(end, weight);
        }
        else
        {
            first->next = new ArcNode(end, weight);
        }
    }
}

/**
 * @description: Prim算法
 * @param begin 最小生成树的开始结点
 * @return void
 */
void Graph::prim(int begin)
{
    /*用于求最小生成树的辅助结构*/
    Assist closedge[20];
    auto start = begin - 1;
    closedge[start].lowcost = 0; // 初始化, U = {u}
    for (int i = 0; i < vexnum; i++)
    {
        if (i != start)
        {
            closedge[i].tail = start;
            auto weig = findArc(start, i + 1);
            if (!weig)
            {
                closedge[i].lowcost = 10000;
            }
            else
            {
                closedge[i].lowcost = weig->weight;
            }
        }
    }
    for (int i = 0; i < vexnum - 1; i++)
    {
        auto minNode = minimum(closedge);
        start = closedge[minNode].tail;
        std::cout << "<" << start + 1 << "," << minNode + 1 << ">" << std::endl;
        closedge[minNode].lowcost = 0;
        for (int j = 0; j < vexnum; j++)
        {
            auto now = findArc(minNode, j + 1);
            if (!now)
            {
                continue;
            }
            if (now->weight < closedge[j].lowcost)
            {
                closedge[j].lowcost = now->weight;
                closedge[j].tail = minNode;
            }
        }
    }
}

int main()
{
    Graph *graph = new Graph();
    graph->createGraph();
    graph->prim(2);
    return 0;
}

注：这里的图用邻接表存储