图的存储结构
前言
图的相关概念可太多了,这里仅记录图的存储结构。
一、邻接矩阵
邻接矩阵需要两个数组来表示一个图,这里我们仅就有向网进行说明。
例如有向网: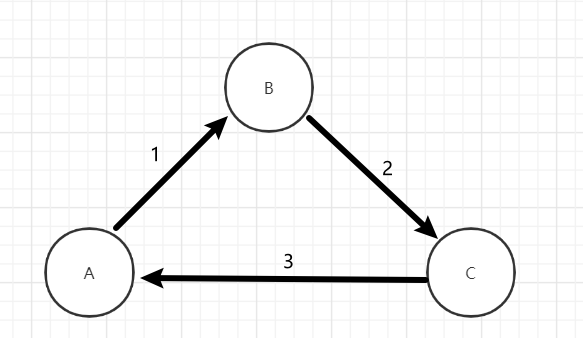

那么它的邻接表表示法,就需要两个数组:
$\begin{pmatrix} A & B & C \end{pmatrix}$ 与 $\begin{pmatrix} ∞& 1& ∞\\ ∞& ∞& 2\\ 3& ∞&∞ \end{pmatrix}$
其中,前一个数组用来表示顶点中的每一个元素,而后一个数组用来表示$<v_i,v_j>$的权值。
代码实现如下
/*
* @Author: zh (RickSchanze) (帝皇の惊)
* @Date: 2022-04-25 19:30:00
* @Description: 图的邻接矩阵表示法
* @LastEditTime: 2022-04-25 20:05:02
*/
#include <iostream>
#define MAX_VERTEX_NUM 20 // vertex 顶点
#define LIMITS 32768
typedef int OtherInfo;
typedef int AdjType;
typedef char VertexData;
enum GraphKind
{
DG, // 有向图
DN, // 有向网
UDG, // 无向图
UDN // 无向网
};
struct ArcNode
{
AdjType adj; // 对于无权图,用0或1表示是否相邻,对于带权图,则为权值类型
OtherInfo info;
};
struct AdjMatrix
{
VertexData vertex[MAX_VERTEX_NUM]; // 顶点向量
ArcNode arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 邻接矩阵
int vexNum; // 顶点数
int arcNum; // 边数
GraphKind kind;
void createDN();
void createDG();
void createUDG();
void createUDN();
int locateVertex(VertexData x); // 求顶点位置的函数
};
/**
* @description 创建一个有向网
* @parameter None
*/
void AdjMatrix::createDN()
{
int i, j, k, weight;
VertexData v1, v2;
std::cin >> this->vexNum >> this->arcNum; //输入图的顶点数和弧数
for (i = 0; i < this->vexNum; i++) // 初始化邻接矩阵
{
for (j = 0; j < this->vexNum; j++)
{
this->arcs[i][j].adj = LIMITS;
}
}
for (i = 0; i < this->vexNum; i++)
{
std::cin >> this->vertex[i]; // 输入图的顶点
}
for (k = 0; k < this->arcNum; k++)
{
std::cin >> v1 >> v2 >> weight; // 一条弧的两个顶点和权值
i = this->locateVertex(v1);
j = this->locateVertex(v2);
this->arcs[i][j].adj = weight;
}
this->kind = GraphKind::DN;
}
void AdjMatrix::createDG()
{
}
void AdjMatrix::createUDG()
{
}
void AdjMatrix::createUDN()
{
}
int AdjMatrix::locateVertex(VertexData x)
{// 找出x在顶点数组中的位置
int j = -1;
for (int i = 0; i < this->vexNum; i++)
{
if (x == this->vertex[i])
{
j = i;
break;
}
}
return j;
}
int main()
{
AdjMatrix *newMartix = new AdjMatrix;
newMartix->createDN();
return 0;
}
这里仅完成了有向网的创建
二、邻接表
邻接表,是将数组与线性表结合起来来存储。
我们仍然需要一个数组来存储顶点,但是顶点结构发生了变化。顶点中会有一个指针指向第一个与它相邻的顶点,这就是表头结点结构的组成。
而在后面的邻接点域中,每一个结点的$data$说明了该结点的表头结点与顶点数组的第$data$个数据相邻,例如对于(1)中的图,它的邻接表是这样的:
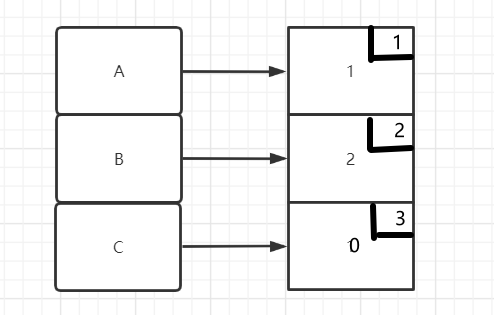
假如我们要用邻接表来表示有向网,那么在邻接表结点中还需要另一个数据包来保存从表头域到该邻接表结点所需要的代价。
代码实现:
/*
* @Author: zh (RickSchanze) (帝皇の惊)
* @Date: 2022-04-25 20:08:14
* @Description: 图的邻接表表示法
* @LastEditTime: 2022-04-25 21:00:29
*/
#include <iostream>
#define MAX_VERTEX_NUM 20 // vertex 顶点
#define LIMITS 32768
typedef int OtherInfo;
typedef int AdjType;
typedef char VertexData;
enum GraphKind
{
DG,
DN,
UDG,
UDN
};
struct ArcNode
{
int adjVex; // 该边/弧指向顶点的位置
ArcNode *nextArc; //指向下一条边/弧的指针
int weight;
};
struct VertexNode
{
VertexData data; // 顶点数据
ArcNode *firstArc; // 指向该顶点第一条边/弧的指针
VertexNode() : firstArc(nullptr){};
};
struct AdjacencyList
{
VertexNode vertex[MAX_VERTEX_NUM];
int vexNum;
int arcNum;
GraphKind kind;
void createDN();
void createDG();
void createUDG();
void createUDN();
int locateVertex(VertexData x); // 求顶点位置的函数
ArcNode *findLastEle(int index);
};
void AdjacencyList::createDN()
{
this->kind = GraphKind::DN;
std::cin >> this->vexNum >> this->arcNum; // 定点数和边数
for (int i = 0; i < this->vexNum; i++)
{
std::cin >> this->vertex[i].data;
}
for (int i = 0; i < this->arcNum; i++)
{
VertexData temp1, temp2;
int weight;
std::cin >> temp1 >> temp2 >> weight;
int m = this->locateVertex(temp1);
int n = this->locateVertex(temp2);
ArcNode *target = this->findLastEle(m);
if (target == nullptr)
{
this->vertex[m].firstArc = new ArcNode;
this->vertex[m].firstArc->weight = weight;
this->vertex[m].firstArc->adjVex = n;
this->vertex[m].firstArc->nextArc = nullptr;
}
else
{
target->nextArc = new ArcNode;
target->nextArc->adjVex = n;
target->nextArc->weight = weight;
target->nextArc->nextArc = nullptr;
}
}
}
/**
* @description: 定位输入元素在顶点数组中的位置
* @param {VertexData} x
* @return {*}
*/
int AdjacencyList::locateVertex(VertexData x)
{
int j = -1;
for (int i = 0; i < this->vexNum; i++)
{
if (x == this->vertex[i].data)
{
j = i;
break;
}
}
return j;
}
/**
* @description: 查找最后一个元素
* @param {int} index
* @return {*}
*/
ArcNode *AdjacencyList::findLastEle(int index)
{
ArcNode *now = this->vertex[index].firstArc;
while (now != nullptr && now->nextArc != nullptr )
{
now = now->nextArc;
}
return now;
}
int main()
{
AdjacencyList *aList = new AdjacencyList;
aList->createDN();
return 0;
}
这里仅实现了有向网的创建。
三、十字链表
十字链表是有向图的另一种存储方式,一个十字链表的展示如下:
对于图:
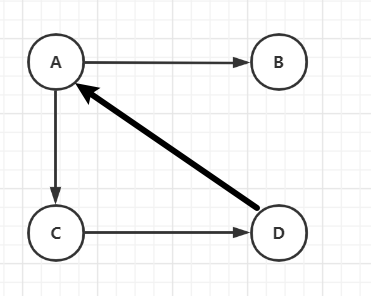
其十字链表存储结构如下:
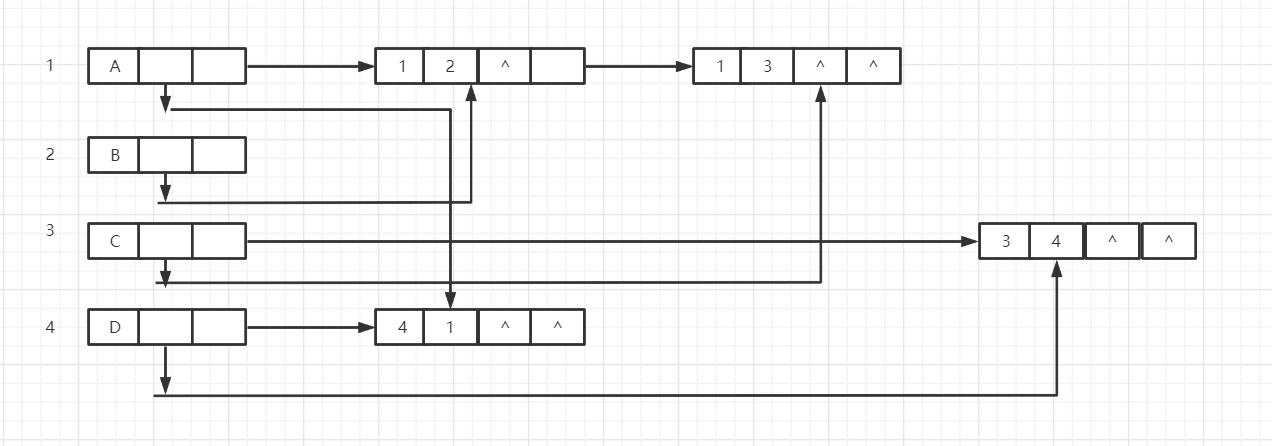
在该十字链表中,我们可以看到表头结点,即标了$1,2,3,4$的四个结点具有两个指针域,第一个指针域,指示以该顶点为弧头的弧,例如A的第一个指针域指向了$(4,1)$,表明该弧以1为弧头
而第二个指针域指示了以该顶点为弧尾的弧,如$(1,2)$,$(1,3)$.
代码实现如下:
/*
* @Author: zh (RickSchanze) (帝皇の惊)
* @Date: 2022-04-27 19:06:00
* @Description:图的十字链表存储法
* @LastEditTime: 2022-04-27 20:19:48
*/
#include <iostream>
struct ArcNode
{
int tailvex; // 弧尾
int headvex; // 弧头
ArcNode *hlink; // 指向与该弧弧头相同的下一条弧
ArcNode *tlink; // 指向与该弧弧尾相同的下一条弧
};
struct VertexNode
{
char data; // 顶点信息,类型自定义
ArcNode *firstin; // 指向以该顶点为弧头的第一个弧顶点
ArcNode *firstout; // 指向以该顶点为弧尾的第一个弧顶点
};
struct OrthList
{
VertexNode vertex[20];
int vexnum;
int arcnum;
void createOrthogonalList(); // orthogonal正交的,直角的
int locateVertex(char x); // 求顶点位置的函数
};
void OrthList::createOrthogonalList()
{
int i, j, k;
std::cin >> this->vexnum >> this->arcnum; // 图顶点数与弧数
for (i = 0; i < this->vexnum; i++)
{
std::cin >> this->vertex[i].data;
this->vertex[i].firstin = nullptr;
this->vertex[i].firstout = nullptr;
}
for (k = 0; k < this->arcnum; k++)
{
char tail, head;
std::cin >> tail >> head;
i = locateVertex(tail);
j = locateVertex(head);
// 新的弧结点
ArcNode *newNode = new ArcNode;
newNode->tailvex = i; // 弧尾为i
newNode->headvex = j; // 为头为j
// 这条弧成为新的弧,插入到原来的,第i个结点的弧尾链(该链中所有结点都以i为弧尾)中,该链可以理解为是水平的
newNode->tlink = this->vertex[i].firstout;
this->vertex[i].firstout = newNode;
// 这条弧成为新的弧,插入到原来的,第j个结点的弧头链(该链中所有结点都以j为弧头)中,该链可以理解为是竖直的
newNode->hlink = this->vertex[j].firstin;
this->vertex[j].firstin = newNode;
}
}
int OrthList::locateVertex(char x)
{
int j = -1;
for (int i = 0; i < this->vexnum; i++)
{
if (x == this->vertex[i].data)
{
j = i;
break;
}
}
return j;
}
int main()
{
OrthList *test = new OrthList;
test->createOrthogonalList();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号